沈阳网络赛
E .
You promised your girlfriend a rounded cake with at least SSS strawberries.
But something goes wrong, you don't have the final cake but an infinite plane with NNN strawberries on it. And you need to draw a circle which contains strawberries completely to make the cake by yourself.
To simplify the problem, the strawberries are represented as circles in 222D plane. Every strawberry has its center (Xi,Yi)(X_i, Y_i)(Xi,Yi) and the same radius RRR.
The cost of your cake is the radius of the circle you draw. So you want to know the minimal cost of the cake, or if you can't give your girlfriend such a cake.
Input
The input file contains several test cases.
The first line of the file is an integer TTT, giving the number of test cases. (T≤20)(T\leq20)(T≤20)
For each test case, there are two integers NNN and SSS in the first line, denoting the number of total strawberries and the number of strawberries on cake as you promised. (1≤N,S≤300)(1\leq N, S \leq 300)(1≤N,S≤300)
In the following NNN lines, each line contains two integers Xi,YiX_i, Y_iXi,Yi, denoting the coordinates of the strawberry center. (0≤Xi,Yi≤10000)(0\leq X_i, Y_i\leq 10000)(0≤Xi,Yi≤10000)
The next line contains one integer RRR, denoting the radius of all strawberries. (1≤R≤10000)(1\leq R \leq 10000)(1≤R≤10000)
It's guaranteed that sum of NNN is smaller than 100010001000.
Output
Output the minimal cost correct to four decimal places if you can make a rounded cake with at least SSS strawberries, or "The cake is a lie." if not.
样例输入
2 5 3 0 0 0 2 2 0 0 0 1 1 1 1 2 0 0 1
样例输出
1.7071 The cake is a lie.
题意 : 给你平面上的 n 个点,问你最少要用半径为多少的圆可以使园内包含 m 个点
思路分析 : 最小圆覆盖板子题
代码示例:
#include <bits/stdc++.h>
using namespace std;
#define Mn 305
const double eps = 1e-7;
const double pi = acos(-1.0);
struct Point
{
double x,y;
Point() {}
Point(double tx,double ty)
{
x=tx;
y=ty;
}
} p[Mn+5];
struct Node
{
double angle;
bool in;
} arc[Mn * Mn + 5];
int n;
double dist(Point p1,Point p2)
{
return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
bool cmp(Node &n1,Node &n2)
{
return n1.angle<n2.angle;
}
double R;
int MaxCircleCover()
{
int ans=1;
for(int i=0;i<n;i++)
{
int cnt=0;
for(int j=0;j<n;j++)
{
if(i==j) continue;
double D = dist(p[i],p[j]);
if(D>2.0*R) continue;
double angle=atan2(p[i].y-p[j].y,p[i].x-p[j].x);
if(angle < 0)
angle += 2 * pi;
double phi=acos(D/(2.0*R));
arc[cnt].angle=angle-phi+ 2 * pi;arc[cnt++].in=true;
arc[cnt].angle=angle+phi+ 2 * pi;arc[cnt++].in=false;
}
sort(arc,arc+cnt,cmp);
int tmp=1;
for(int j=0;j<cnt;j++)
{
if(arc[j].in) tmp++;
else tmp--;
ans=max(ans,tmp);
}
}
return ans;
}
int main()
{
int t;scanf("%d",&t);
while(t--)
{
int s;
scanf("%d%d",&n,&s);
for(int i=0;i<n;i++)
scanf("%lf%lf",&p[i].x,&p[i].y);
double r;
scanf("%lf",&r);
double l1=0,r1=100000;
if(n<s)
{
printf("The cake is a lie.\n");continue;
}
while(abs(r1-l1)>eps)
{
double mid=(l1+r1)*0.5;
R=mid;
int p=MaxCircleCover();
if(p>=s)
{
r1=mid;
}
else
{
l1=mid;
}
}
printf("%.4lf\n",l1+r);
}
return 0;
}
G .
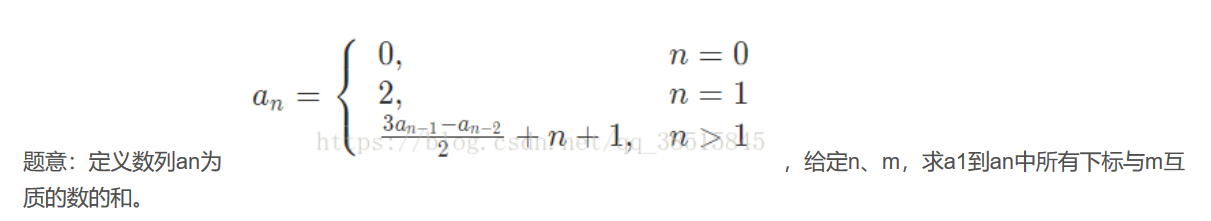
思路分析 :
一个长整型数字他的质因子最多只有 10 个,且分解的次数不会超过 40 次
再计算 1-n 中与 m 互质的情况下,可以用经典的容斥原理,这里有一个二进制的优化
代码示例 :
#define ll long long
const ll maxn = 1e6+5;
const ll mod = 1e9+7;
const ll inv6 = 166666668;
const ll inv2 = 500000004;
ll n, m;
ll prime[100];
ll cnt;
void getprime(){
cnt = 0; ll num = m;
for(ll i = 2; i*i <= m; i++){
if (num%i == 0) {
prime[cnt++] = i;
while(num%i == 0){
num /= i;
}
}
if (num == 1) break;
}
if (num > 1) prime[cnt++] = num;
}
ll cal1(ll tem, ll x){
ll ans = tem*tem%mod*x%mod*(x+1)%mod*(2*x+1)%mod*inv6%mod;
return ans;
}
ll cal2(ll tem, ll x){
ll ans = tem*x%mod*(x+1)%mod*inv2%mod;
return ans;
}
void solve() {
ll ans = 0;
for(ll i = 1; i < (1<<cnt); i++){
ll f = 0; ll tem = 1;
for(ll j = 0; j < cnt; j++){
if (i&(1<<j)) {
f++;
tem *= prime[j];
}
}
ll time = n/tem;
if (f&1) ans = (ans+cal1(tem, time)+cal2(tem, time))%mod;
else ans = (ans-cal1(tem, time)-cal2(tem, time))%mod;
ans = (ans+mod)%mod;
}
ll sum = (cal1(1, n)+cal2(1, n))%mod;
ans = (sum-ans)%mod;
printf("%lld\n", (ans+mod)%mod);
}
int main() {
while(~scanf("%lld%lld", &n, &m)){
getprime();
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号