2018 南京网络赛
B.
Feeling hungry, a cute hamster decides to order some take-away food (like fried chicken for only 303030 Yuan).
However, his owner CXY thinks that take-away food is unhealthy and expensive. So she demands her hamster to fulfill a mission before ordering the take-away food. Then she brings the hamster to a wall.
The wall is covered by square ceramic tiles, which can be regarded as a n∗mn * mn∗m grid. CXY wants her hamster to calculate the number of rectangles composed of these tiles.
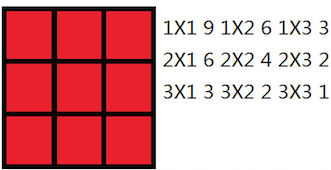
For example, the following 3∗33 * 33∗3 wall contains 363636 rectangles:
Such problem is quite easy for little hamster to solve, and he quickly manages to get the answer.
Seeing this, the evil girl CXY picks up a brush and paint some tiles into black, claiming that only those rectangles which don't contain any black tiles are valid and the poor hamster should only calculate the number of the valid rectangles. Now the hamster feels the problem is too difficult for him to solve, so he decides to turn to your help. Please help this little hamster solve the problem so that he can enjoy his favorite fried chicken.
Input
There are multiple test cases in the input data.
The first line contains a integer TTT : number of test cases. T≤5T \le 5T≤5.
For each test case, the first line contains 333 integers n,m,kn , m , kn,m,k , denoting that the wall is a n×mn \times mn×m grid, and the number of the black tiles is kkk.
For the next kkk lines, each line contains 222 integers: x yx\ yx y ,denoting a black tile is on the xxx-th row and yyy-th column. It's guaranteed that all the positions of the black tiles are distinct.
For all the test cases,
1≤n≤105,1≤m≤1001 \le n \le 10^5,1\le m \le 1001≤n≤105,1≤m≤100,
0≤k≤105,1≤x≤n,1≤y≤m0 \le k \le 10^5 , 1 \le x \le n, 1 \le y \le m0≤k≤105,1≤x≤n,1≤y≤m.
It's guaranteed that at most 222 test cases satisfy that n≥20000n \ge 20000n≥20000.
Output
For each test case, print "Case #xxx: ansansans" (without quotes) in a single line, where xxx is the test case number and ansansans is the answer for this test case.
Hint
The second test case looks as follows:
样例输入
2 3 3 0 3 3 1 2 2
样例输出
Case #1: 36 Case #2: 20
思路 : 点此处
E .
Dlsj is competing in a contest with n(0<n≤20)n (0 < n \le 20)n(0<n≤20) problems. And he knows the answer of all of these problems.
However, he can submit iii-th problem if and only if he has submitted (and passed, of course) sis_isi problems, the pi,1p_{i, 1}pi,1-th, pi,2p_{i, 2}pi,2-th, ........., pi,sip_{i, s_i}pi,si-th problem before.(0<pi,j≤n,0<j≤si,0<i≤n)(0 < p_{i, j} \le n,0 < j \le s_i,0 < i \le n)(0<pi,j≤n,0<j≤si,0<i≤n) After the submit of a problem, he has to wait for one minute, or cooling down time to submit another problem. As soon as the cooling down phase ended, he will submit his solution (and get "Accepted" of course) for the next problem he selected to solve or he will say that the contest is too easy and leave the arena.
"I wonder if I can leave the contest arena when the problems are too easy for me."
"No problem."
—— CCF NOI Problem set
If he submits and passes the iii-th problem on ttt-th minute(or the ttt-th problem he solve is problem iii), he can get t×ai+bit \times a_i + b_it×ai+bi points. (∣ai∣,∣bi∣≤109)(|a_i|, |b_i| \le 10^9)(∣ai∣,∣bi∣≤109).
Your task is to calculate the maximum number of points he can get in the contest.
Input
The first line of input contains an integer, nnn, which is the number of problems.
Then follows nnn lines, the iii-th line contains si+3s_i + 3si+3 integers, ai,bi,si,p1,p2,...,psia_i,b_i,s_i,p_1,p_2,...,p_{s_i}ai,bi,si,p1,p2,...,psias described in the description above.
Output
Output one line with one integer, the maximum number of points he can get in the contest.
Hint
In the first sample.
On the first minute, Dlsj submitted the first problem, and get 1×5+6=111 \times 5 + 6 = 111×5+6=11 points.
On the second minute, Dlsj submitted the second problem, and get 2×4+5=132 \times 4 + 5 = 132×4+5=13 points.
On the third minute, Dlsj submitted the third problem, and get 3×3+4=133 \times 3 + 4 = 133×3+4=13 points.
On the forth minute, Dlsj submitted the forth problem, and get 4×2+3=114 \times 2 + 3 = 114×2+3=11 points.
On the fifth minute, Dlsj submitted the fifth problem, and get 5×1+2=75 \times 1 + 2 = 75×1+2=7 points.
So he can get 11+13+13+11+7=5511+13+13+11+7=5511+13+13+11+7=55 points in total.
In the second sample, you should note that he doesn't have to solve all the problems.
样例输入1
5 5 6 0 4 5 1 1 3 4 1 2 2 3 1 3 1 2 1 4
样例输出1
55
样例输入2
1 -100 0 0
样例输出2
0
题意 : 告诉你 n 个问题,回答每个问题会有一些限制条件,并且回答后会有相应的分数,问最终最大的得分是多少?
思路分析 :
一看数据范围 n <= 20 , 显然装压了,然后从头开始枚举即可,枚举当前状态是什么,然后去转移一下它可以到达哪些状态
以后写代码的时候,位运算这块记得加些括号什么的,容易错
代码示例 :
#define ll long long
const ll maxn = 1e6+5e5;
const ll mod = 1e9+7;
const double eps = 1e-9;
const double pi = acos(-1.0);
const ll inf = -(1ll)<<60;
ll n;
ll a[30], b[30], state[30];
ll bit[30], numbit[maxn];
ll dp[maxn];
void init() {
bit[0] = 1;
for(ll i = 1; i <= 20; i++) bit[i] = bit[i-1]<<1;
numbit[0] = 0;
ll N = 1<<20;
for(ll i = 1; i <= N; i++){
numbit[i] = 1+numbit[i&(i-1)];
}
}
void solve() {
for(int i = 0; i < (1<<n); i++) dp[i] = inf;
dp[0] = 0;
ll ans = 0;
for(ll i = 0; i < (1<<n); i++){
if (dp[i] == inf) continue;
ans = max(ans, dp[i]);
for(ll j = 1; j <= n; j++){
if (bit[j-1]&i) continue;
if ((i & state[j]) != state[j]) continue;
dp[i|bit[j-1]] = max(dp[i|bit[j-1]], dp[i]+numbit[i|bit[j-1]]*a[j]+b[j]);
}
}
printf("%lld\n", ans);
}
int main() {
//freopen("in.txt", "r", stdin);
//freopen("out.txt", "w", stdout);
ll s;
init();
cin >> n;
for(ll i = 1; i <= n; i++){
scanf("%lld%lld%lld", &a[i], &b[i], &s);
ll num = 0, x;
while(s--){
scanf("%lld", &x);
num += bit[x-1];
}
state[i] = num;
}
solve();
return 0;
}
A number is skr, if and only if it's unchanged after being reversed. For example, "12321", "11" and "1" are skr numbers, but "123", "221" are not. FYW has a string of numbers, each substring can present a number, he wants to know the sum of distinct skr number in the string. FYW are not good at math, so he asks you for help.
Input
The only line contains the string of numbers SSS.
It is guaranteed that 1≤S[i]≤91 \le S[i] \le 91≤S[i]≤9, the length of SSS is less than 200000020000002000000.
Output
Print the answer modulo 100000000710000000071000000007.
样例输入1
111111
样例输出1
123456
样例输入2
1121
样例输出2
135
------------------------------------
题意 : 将串中所有本质不同的串进行累加求和
思路分析 :
比赛的时候写了一个 马拉车+hash , 有一些小地方用 map 判重,超时了,就想着改成 hash 拉链,结果 gg 了,调了几天了终于好了,下次再不能偷懒全部定义成 unsigned long long了,可能有些地方会是负值,但是这样我们就会计算错误了
manacher 有一个重要的性质就是他在走的过程中会把所有本质不同的串至少走一遍,而且一个长度为 n 的字符串,本质不同的字符串个数不会超过 n 。
代码示例 :
using namespace std;
#define ll long long
#define ull unsigned long long
const ll maxn = 2e6+50;
const ll mod = 1e9+7;
const ll mm = 4000007;
const double eps = 1e-9;
const double pi = acos(-1.0);
const ll inf = 0x3f3f3f3f;
char s[maxn], now[maxn<<1];
ll len;
ll p[maxn<<1];
ull _hash[maxn];
ull pq = 19873, pp[maxn];
ll yy[maxn], fac[maxn];
void init() {
for(ll i = 1; i <= len; i++){
_hash[i] = _hash[i-1]*pq+(s[i]-'a');
}
pp[0] = 1;
for(ll i = 1; i <= 2000000; i++) pp[i]=pp[i-1]*pq;
fac[0] = 1;
for(ll i = 1; i <= 2000000; i++) {
fac[i] = fac[i-1]*10%mod;
yy[i] = yy[i-1]*10+(s[i]-'0');
yy[i] %= mod;
}
}
struct node
{
ll x;
ll next;
}arr[maxn];
ll head[maxn<<1]; // !!!
ll tot = 0;
ll ans = 0;
ll getnum(ll l, ll r){
ll x = yy[r]-yy[l-1]*fac[r-l+1]%mod; // !!!
x %= mod;
x = (x+mod)%mod;
return x;
}
void insert(ll l, ll r){
ll num = _hash[r]-_hash[l-1]*pp[r-l+1];
ll num2 = num%mm;
num2 = (num2+mm)%mm;
ll f = head[num2];
while(f != -1){
if (arr[f].x == num) return;
f = arr[f].next;
}
arr[tot].next = head[num2];
arr[tot].x = num;
head[num2] = tot++;
ans += getnum(l, r);
ans %= mod;
}
void manacher() {
now[0] = '$';
for(ll i = 1; i <= 2*len; i += 2){
now[i] = '#';
now[i+1] = s[(i+1)/2];
}
now[2*len+1] = '#';
now[2*len+2] = '@';
now[2*len+3] = '\0';
ll len2 = len*2+1;
ll mx = 0, id = 0;
for(ll i = 1; i <= len2; i++){
if (i <= mx) p[i] = min(p[2*id-i], mx-i);
else p[i] = 1;
while(i+p[i]<=len2 && i-p[i]>=1 && now[i-p[i]] == now[i+p[i]]) {
ll l = (i-p[i]+1)/2, r = (i+p[i])/2;
insert(l, r);
p[i]++;
}
if (mx < i+p[i]) {mx = i+p[i]; id = i;}
}
printf("%lld\n", ans);
}
int main() {
memset(head, -1, sizeof(head));
scanf("%s", s+1);
len = strlen(s+1);
init();
manacher();
return 0;
}
G .
During tea-drinking, princess, amongst other things, asked why has such a good-natured and cute Dragon imprisoned Lpl in the Castle? Dragon smiled enigmatically and answered that it is a big secret. After a pause, Dragon added:
— We have a contract. A rental agreement. He always works all day long. He likes silence. Besides that, there are many more advantages of living here in the Castle. Say, it is easy to justify a missed call: a phone ring can't reach the other side of the Castle from where the phone has been left. So, the imprisonment is just a tale. Actually, he thinks about everything. He is smart. For instance, he started replacing incandescent lamps with energy-saving lamps in the whole Castle...
Lpl chose a model of energy-saving lamps and started the replacement as described below. He numbered all rooms in the Castle and counted how many lamps in each room he needs to replace.
At the beginning of each month, Lpl buys mmm energy-saving lamps and replaces lamps in rooms according to his list. He starts from the first room in his list. If the lamps in this room are not replaced yet and Lpl has enough energy-saving lamps to replace all lamps, then he replaces all ones and takes the room out from the list. Otherwise, he'll just skip it and check the next room in his list. This process repeats until he has no energy-saving lamps or he has checked all rooms in his list. If he still has some energy-saving lamps after he has checked all rooms in his list, he'll save the rest of energy-saving lamps for the next month.
As soon as all the work is done, he ceases buying new lamps. They are very high quality and have a very long-life cycle.
Your task is for a given number of month and descriptions of rooms to compute in how many rooms the old lamps will be replaced with energy-saving ones and how many energy-saving lamps will remain by the end of each month.
Input
Each input will consist of a single test case.
The first line contains integers nnn and m(1≤n≤100000,1≤m≤100)m (1 \le n \le 100000, 1 \le m \le 100)m(1≤n≤100000,1≤m≤100) — the number of rooms in the Castle and the number of energy-saving lamps, which Lpl buys monthly.
The second line contains nnn integers k1,k2,...,knk_1, k_2, ..., k_nk1,k2,...,kn
(1≤kj≤10000,j=1,2,...,n)(1 \le k_j \le 10000, j = 1, 2, ..., n)(1≤kj≤10000,j=1,2,...,n) — the number of lamps in the rooms of the Castle. The number in position jjj is the number of lamps in jjj-th room. Room numbers are given in accordance with Lpl's list.
The third line contains one integer q(1≤q≤100000)q (1 \le q \le 100000)q(1≤q≤100000) — the number of queries.
The fourth line contains qqq integers d1,d2,...,dqd_1, d_2, ..., d_qd1,d2,...,dq
(1≤dp≤100000,p=1,2,...,q)(1 \le d_p \le 100000, p = 1, 2, ..., q)(1≤dp≤100000,p=1,2,...,q) — numbers of months, in which queries are formed.
Months are numbered starting with 111; at the beginning of the first month Lpl buys the first m energy-saving lamps.
Output
Print qqq lines.
Line ppp contains two integers — the number of rooms, in which all old lamps are replaced already, and the number of remaining energy-saving lamps by the end of dpd_pdp month.
Hint
Explanation for the sample:
In the first month, he bought 444 energy-saving lamps and he replaced the first room in his list and remove it. And then he had 111 energy-saving lamps and skipped all rooms next. So, the answer for the first month is 1,1−−−−−−11,1------11,1−−−−−−1 room's lamps were replaced already, 111 energy-saving lamp remain.
样例输入
5 4 3 10 5 2 7 10 5 1 4 8 7 2 3 6 4 7
样例输出
4 0 1 1 3 6 5 1 5 1 2 0 3 2 4 4 3 6 5 1
题意 : 给你 n 个要换屋子,告诉你每个屋子有多少个灯泡要更换,同时每个月会买进 m 个灯泡,每次更换时要求是从左向右寻找第一个符合条件的屋子去更换即可,若此月可以一直此过程,则一直下去
思路分析 : 简直就是个阅读题,题目一读完多简单...然而我并没有读对题意,读成了每次必须更换整个区间中比其稍大的灯泡....
代码示例:
#define ll long long
const ll maxn = 1e5+5;
const ll mod = 1e9+7;
const double eps = 1e-9;
const double pi = acos(-1.0);
const ll inf = 0x3f3f3f3f;
#define lson k<<1
#define rson k<<1|1
ll n, m;
struct node
{
ll l, r;
ll mi;
}t[maxn<<2];
void build(ll l, ll r, ll k){
t[k].l = l, t[k].r = r;
if (l == r) {
ll x;
scanf("%lld", &x);
t[k].mi = x;
return;
}
ll mid = (l+r)>>1;
build(l, mid, lson);
build(mid+1, r, rson);
t[k].mi = min(t[lson].mi, t[rson].mi);
}
ll a1[maxn], a2[maxn];
ll f, sum, p;
void query(ll k){
if (t[k].l == t[k].r){
f = t[k].mi;
t[k].mi = inf;
return;
}
else if (t[lson].mi <= sum){
query(lson);
}
else if (t[rson].mi <= sum){
query(rson);
}
t[k].mi = min(t[lson].mi, t[rson].mi);
}
void solve(){
sum = 0;
ll cc = 0;
for(ll i = 1; i <= 100000; i++){
if (t[1].mi != inf) {
sum += m;
f = 999;
while(f != 0) {
f = 0;
query(1);
if (f != 0) {
cc++, sum = sum-f;
}
}
}
a1[i] = cc, a2[i] = sum;
}
}
int main() {
//freopen("in.txt", "r", stdin);
//freopen("out.txt", "w", stdout);
ll q, x;
cin >> n >> m;
build(1, n, 1);
cin >> q;
solve();
while(q--){
scanf("%lld", &x);
printf("%lld %lld\n", a1[x], a2[x]);
}
return 0;
}
L .
There are NNN cities in the country, and MMM directional roads from uuu to v(1≤u,v≤n)v(1\le u, v\le n)v(1≤u,v≤n). Every road has a distance cic_ici. Haze is a Magical Girl that lives in City 111, she can choose no more than KKK roads and make their distances become 000. Now she wants to go to City NNN, please help her calculate the minimum distance.
Input
The first line has one integer T(1≤T≤5)T(1 \le T\le 5)T(1≤T≤5), then following TTT cases.
For each test case, the first line has three integers N,MN, MN,M and KKK.
Then the following MMM lines each line has three integers, describe a road, Ui,Vi,CiU_i, V_i, C_iUi,Vi,Ci. There might be multiple edges between uuu and vvv.
It is guaranteed that N≤100000,M≤200000,K≤10N \le 100000, M \le 200000, K \le 10N≤100000,M≤200000,K≤10,
0≤Ci≤1e90 \le C_i \le 1e90≤Ci≤1e9. There is at least one path between City 111 and City NNN.
Output
For each test case, print the minimum distance.
样例输入
1 5 6 1 1 2 2 1 3 4 2 4 3 3 4 1 3 5 6 4 5 2
样例输出
3
题意 : 给你一张正常的图,求从 1 到 n 的最短路,最多可以将 k 条边的长度变为0,求最短距离
思路分析 : dij 的板子题,区别一点就是当前点出发的时候将不将此边变为 0 即可,写的过程中没有加 vis 标记,一直超内存!!!
代码示例 :
#define ll long long
const ll maxn = 1e5+5;
const ll maxm = 2e5+5;
const ll mod = 1e9+7;
const double eps = 1e-9;
const double pi = acos(-1.0);
const ll inf = 0x3f3f3f3f;
ll n, m, k;
struct node
{
int next;
int to, cost;
}edge[maxm];
ll dp[maxn][15], vis[maxn][15];
struct p
{
ll x, b, c;
bool operator< (const p &v)const{
return c>v.c;
}
};
priority_queue<p>que;
ll cnt;
ll head[maxn];
void init(){
cnt = 0;
memset(head, -1, sizeof(head));
}
void add(int u, int v, int w){
edge[cnt].next = head[u];
edge[cnt].to = v;
edge[cnt].cost = w;
head[u] = cnt++;
}
void dij() {
memset(dp, inf, sizeof(dp));
memset(vis, false, sizeof(vis));
while(!que.empty()) que.pop();
dp[1][0] = 0;
que.push({1, 0, 0});
while(!que.empty()){
p v = que.top();
que.pop();
if (vis[v.x][v.b]) continue;
vis[v.x][v.b] = true;
for(ll i = head[v.x]; i != -1; i = edge[i].next){
ll to = edge[i].to;
ll cost = edge[i].cost;
dp[to][v.b] = min(dp[to][v.b], dp[v.x][v.b]+cost);
if (!vis[to][v.b]) que.push({to, v.b, dp[to][v.b]});
if (v.b < k) {
dp[to][v.b+1] = min(dp[to][v.b+1], dp[v.x][v.b]);
if (!vis[to][v.b+1])que.push({to, v.b+1, dp[to][v.b+1]});
}
}
}
}
int main() {
//freopen("in.txt", "r", stdin);
//freopen("out.txt", "w", stdout);
ll t;
ll a, b, c;
cin >> t;
while(t--){
cin >> n >> m >> k;
init();
while(m--){
scanf("%lld%lld%lld", &a, &b, &c);
add(a, b, c);
}
dij();
ll ans = inf;
for(ll i = 0; i <= k; i++) ans = min(ans, dp[n][i]);
printf("%lld\n", ans);
//printf("==== %lld\n", cnt);
}
return 0;
}