状压 + 背包

Description

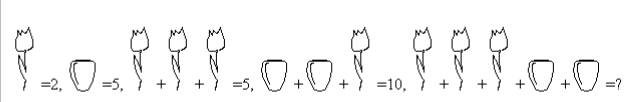
In a shop each kind of product has a price. For example, the price of a flower is 2 ICU (Informatics Currency Units) and the price of a vase is 5 ICU. In order to attract more customers, the shop introduces some special offers.
A special offer consists of one or more product items for a reduced price. Examples: three flowers for 5 ICU instead of 6, or two vases together with one flower for 10 ICU instead of 12.
Write a program that calculates the price a customer has to pay for certain items, making optimal use of the special offers. That is, the price should be as low as possible. You are not allowed to add items, even if that would lower the price.
For the prices and offers given above, the (lowest) price for three flowers and two vases is 14 ICU: two vases and one flower for the reduced price of 10 ICU and two flowers for the regular price of 4 ICU.

Input

Your program is to read from standard input. The first line contains the number b of different kinds of products in the basket (0 <= b <= 5). Each of the next b lines contains three values c, k, and p. The value c is the (unique) product code (1 <= c <= 999). The value k indicates how many items of this product are in the basket (1 <= k <= 5). The value p is the regular price per item (1 <= p <= 999). Notice that all together at most 5*5=25 items can be in the basket. The b+2nd line contains the number s of special offers (0 <= s <= 99). Each of the next s lines describes one offer by giving its structure and its reduced price. The first number n on such a line is the number of different kinds of products that are part of the offer (1 <= n <= 5). The next n pairs of numbers (c,k) indicate that k items (1 <= k <= 5) with product code c (1 <= c <= 999) are involved in the offer. The last number p on the line stands for the reduced price (1 <= p <= 9999). The reduced price of an offer is less than the sum of the regular prices.

Output

Your program is to write to standard output. Output one line with the lowest possible price to be paid.

Sample Input

2
7 3 2
8 2 5
2
1 7 3 5
2 7 1 8 2 10

Sample Output

14

题意：超市里面有一些商品，商品有任意多个，再给你这个人的购物清单，并且在超市里会不定期有一些打折促销的活动，购买一些指定组合的商品会有优惠折扣，但是要求这个人所购买的全部商品数量必须恰好是指定的。
思路分析：因为商品只有 5 种，比较好想到的就是整一个 5维的 dp背包，想一想还有没有更优的方案，最多有5种商品，并且每种商品最多有5个，那么不就可以压缩为5位6进制的数了吗，表示此时的状态。然后转变为一个完全背包。
代码示例：

int n, m;
map<int, int>mp;
struct node
{
    int s; // 状态
    int cost; // 花费
}pre[120];
int dp[10000];
int pp[10];
void init(){
    pp[0] = 1;
    for(int i = 1; i <= 6; i++) pp[i] = pp[i-1]*6;
}

int main() {
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    int a, b, c;
    int state=0;
    int k = 1;
    init();
    
    cin >> n;
    for(int i = 1; i <= n; i++){
        scanf("%d%d%d", &a, &b, &c);
        mp[a] = i-1;
        state += b*pp[i-1];     
        pre[k].s = pp[i-1];
        pre[k++].cost = c;    
    }
    //printf("%d\n", state);
    
    cin >> m;
    int id, cnt;
    for(int i = 1; i <= m; i++){
        scanf("%d", &a);
        int sum = 0;
        for(int j = 1; j <= a; j++){
            scanf("%d%d", &id, &cnt);
            sum += pp[mp[id]]*cnt;
        }
        scanf("%d", &c);
        pre[k].s = sum;
        pre[k++].cost = c;
    }
    
    memset(dp, inf, sizeof(dp));
    dp[0] = 0;
    for(int i = 1; i < k; i++){
        for(int j = pre[i].s; j <= state; j++){
            dp[j] = min(dp[j], dp[j-pre[i].s]+pre[i].cost);
        }
    }    
    printf("%d\n", dp[state]);
    return 0;
    
}