欧拉公式 （平面）

欧拉公式的表述是这样的 V+F-E = 2, V 表示点的数量， F表示面的数量， E表示边的数量

 

一道新疆区域赛的题， 凉...

Farmer John owns a farm. He first builds a circle fence. Then, he will choose n points and build some straight fences connecting them. Next, he will feed a cow in each region so that cows cannot play with each other without breaking the fences. In order to feed more cows, he also wants to have as many regions as possible. However, he is busy building fences now, so he needs your help to determine what is the maximum number of cows he can feed if he chooses these n points properly.

Input

The first line contains an integer 1≤T≤1000001 \le T \le 1000001≤T≤100000, the number of test cases. For each test case, there is one line that contains an integer n. It is guaranteed that 1≤T≤1051 \le T \le 10^5 1≤T≤105 and 1≤n≤10181 \le n \le 10^{18}1≤n≤1018.

Output

For each test case, you should output a line ”Case #iii: ans” where iii is the test caseS number, starting from 111 and ans is the remainder of the maximum number of cows farmer John can feed when divided by 109+710^9 + 7109+7.

样例输入

3
1
3
5

样例输出

Case #1: 1
Case #2: 4
Case #3: 16

题意 ： 给你 n 个点，任意两个点之间都可以连线，问最多可以将平面分成多少块？
直接套用一个欧拉公式就可以，计算出来点和边，面就直接可以推出来，不过最后得到的答案是要再减去 1 的，因为平面外围是一个无限大的面。
思路就是从任意一个点出发，枚举直线，枚举得第一条直线左边 0 个点， 右边 n-2 个点，显然不会再这条直线上产生交点，枚举第二条直线，左边一个点，右边 n-2-1 个点，会再这条直线上产生 1*(n-2-i)个点
累加计算就可以，计算边得时候也是一样得

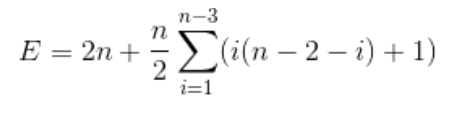
由 V + F - E = 2 知 F+1 = E - V + 2

代入化简得

代码示例 ：

#define ll unsigned long long
const ll mod = 1e9+7;

ll n;

ll qpow(ll x, ll p){
    ll res = 1;
    
    while(p > 0){
        if (p&1) res *= x;
        res %= mod;
        x *= x;
        x %= mod;
        p >>= 1;
    }
    return res%mod;
}

ll solve(){
    ll s1 = 1;
    for(int i = 1; i <= 4; i++){
        s1 *= n;
        s1 %= mod;
    }
    ll s2 = 1;
    for(int i = 1; i <= 3; i++){
        s2 *= n;
        s2 %= mod;
    }
    s2 *= 6;  
    s2 %= mod;  // !!! 因为这里 WA 了几次， 不然下面得减法取模会有问题
    ll s3 = 1;
    for(int i = 1; i <= 2; i++){
        s3 *= n;
        s3 %= mod;
    }
    s3 *= 23;
    s3 %= mod;
    ll s4 = 18*n%mod;
    
    ll s = ((s1-s2+mod)%mod+(s3-s4+mod)%mod)%mod;
    ll f = qpow(24, mod-2)%mod;
    ll ans = ((s*f)%mod+1)%mod;
    return ans;
}

int main() {
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    int t;
    int kase = 1;
    
    cin >>t;
    while(t--){
        scanf("%llu", &n);
        n %= mod; 
        printf("Case #%d: ", kase++);
        if (n == 1) printf("1\n");
        else if (n == 2) printf("2\n");
        else if (n == 3) printf("4\n");
        else printf("%llu\n", solve());    
    }
    return 0;
}