卡特兰数入门

推荐博客 ： https://blog.csdn.net/qq_26525215/article/details/51453493

　　　　　  https://blog.csdn.net/doc_sgl/article/details/8880468

 　　　　　 http://www.jb51.net/article/37511.htm

 

卡特兰数是一个出现在组合数学中的数列

卡特兰数前 20 项为 ：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190

递推公式如下 ： F(n+1) = (4*n - 6)*F(n) / n

 

 

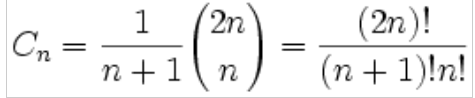
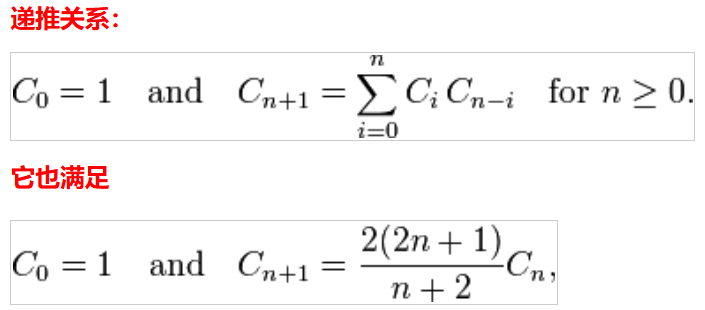
判断一个问题是不是此类问题，有两种比较思考的方向

1 . 将整个问题简化为一个只有 01 的数列，例如括号匹配的问题，

 n 组括号合法的运算式的个数 ， 将左括号看成 0 ，右括号看成 1 ，所以总的方案是C（2n, n）， 则任意一个合法的序列在奇数位置上不能有 1 ，当不合法时，将不合法位置到开头的位置全部反置，则这样处理后的 0 的个数将变成 n+1 ， 1 的个数变成 n-1 , 此种排列组合对应着一组不合法的解， 是C(2n-1, n) ， 两式相减即可

2 . 第二种就是要从卡特兰数的定义出发， f(n) = f(0)*f(n) + f(1)*f(n-1) +...+ f(n)*f(0)

求一个凸多边形区域划分成三角形区域的方法数？

以凸多边形的一边为基，设这条边的2个顶点为A和B。从剩余顶点中选1个，可以将凸多边形分成三个部分，中间是一个三角形，左右两边分别是两个凸多边形，然后求解左右两个凸多边形。
      设问题的解f(n)，其中n表示顶点数，那么f(n) = f(2)*f(n-1) + f(3)*f(n-2) + ......f(n-2)*f(3) + f(n-1)*f(2)。f(2)*f(n-1)表示三个相邻的顶点构成一个三角形，那么另外两个部分的顶点数分别为2和n-1。