枚举 + exgcd
题意:已知xi=(a*xi-1+b) mod 10001,且告诉你x1,x3.........x2*t-1,让你求出其偶数列
思路分析 : 题目所要求的的是对 10001 取余,由模运算的性质可知,a 在经过取模后一定是 0 - 10000 范围内的一个数,那么我们就可以枚举 a
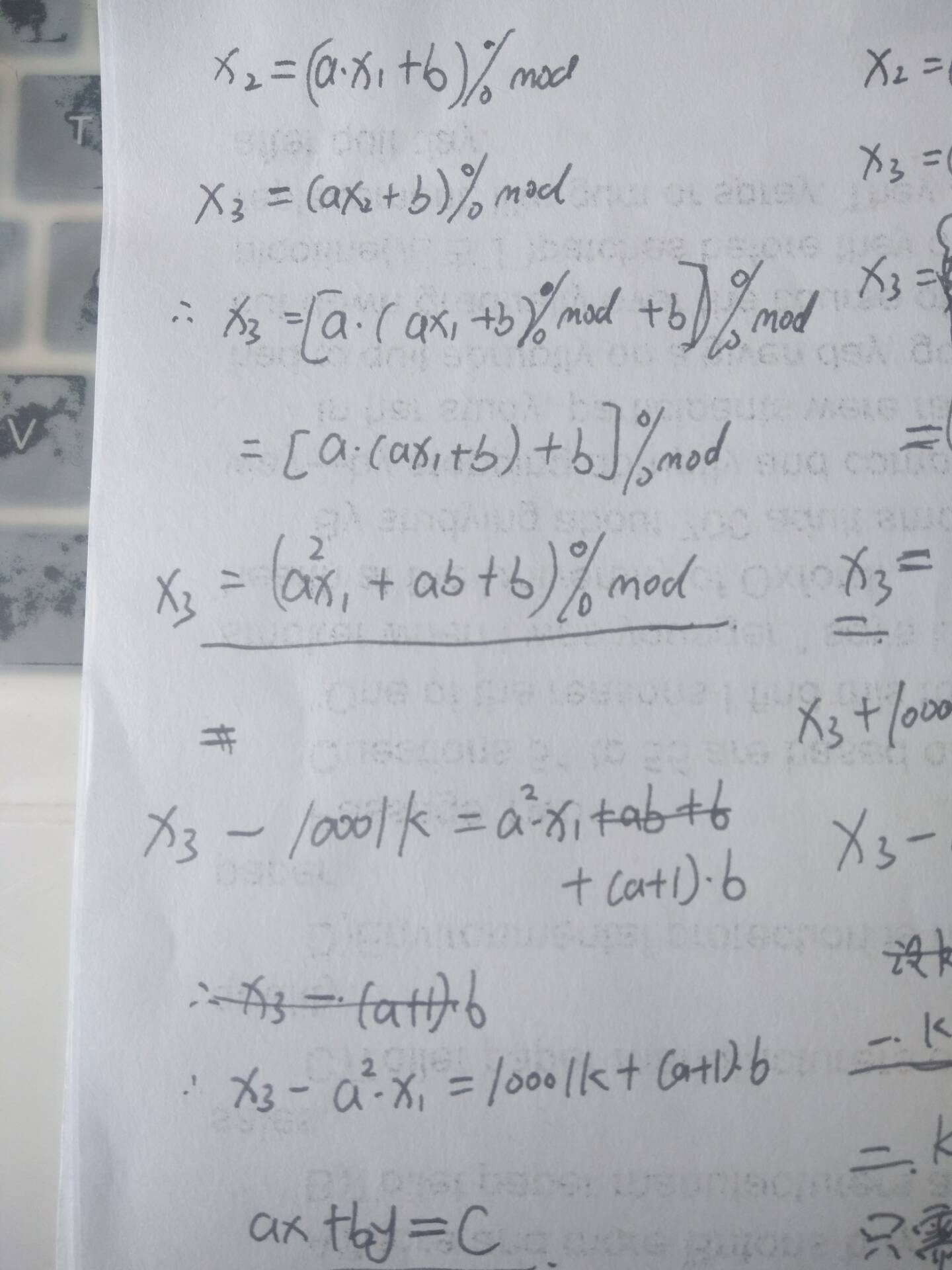
在利用 x2, x3 的式子代入化简,最终得到的式子是类似 exgcd 的,直接求就可以。
代码示例 :
#define ll long long
const ll maxn = 1e6+5;
const ll mod = 10001;
const double eps = 1e-9;
const double pi = acos(-1.0);
const ll inf = 0x3f3f3f3f;
ll n;
ll pre[105];
ll mid[205];
void exgcd(ll a, ll b, ll &g, ll &x, ll &y){
if (b == 0){ g = a; x = 1; y = 0;}
else {exgcd(b, a%b, g, y, x); y -= x*(a/b);}
}
int main() {
//freopen("in.txt", "r", stdin);
//freopen("out.txt", "w", stdout);
cin >> n;
for(ll i = 1; i <= n; i++){
scanf("%lld", &pre[i]);
}
ll g, b, k;
for(ll i = 0; i <= 10000; i++){
ll f = (pre[2]-i*i*pre[1]);
exgcd(mod, i+1, g, k, b);
if (f % g) continue;
b = b*(f/g)%mod;
mid[1] = pre[1];
for(ll j = 2; j <= 2*n; j++){
mid[j] = (i*mid[j-1]+b+mod)%mod;
}
ll sign = 0;
for(ll j = 1; j <= 2*n; j += 2){
if (mid[j] != pre[(j+1)/2]){
sign = 1; break;
}
}
if (!sign){
break;
}
}
for(ll j = 2; j <= 2*n; j += 2){
printf("%lld\n", mid[j]);
}
return 0;
}
东北日出西边雨 道是无情却有情


 浙公网安备 33010602011771号
浙公网安备 33010602011771号