斯特林公式

先想一个简单的问题

　　让你去求一个任意一个数 x 在 a 进制下的位数， 那么答案就是 log(a)(x) + 1, (以 a 为底 x 的对数 + 1 )

现在让你去求 n！ 在 a 进制下的位数 答案就是 log(a)( n! ) = log(a)(1*2*3*...*n) = log(a)(1) + log(a)(2) + log(a)(3) + ... + log(a)(n) . 最后在取整 + 1

这种做法的复杂度是 n *log n ,当 n 很大时显然是不可取的，斯特林公示是对此的一个优化

int main() {
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    int x;
    
    while(~scanf("%d", &x)){
        double ans = 0;
        int s = 1;
        for(int i = 1; i <= x; i++){
            ans += log10(i);
            s *= i;
        }        
        printf("%d  ", s);
        printf("%d\n", (int)(ans)+1);
    }
    return 0;
}

 

斯特林公式

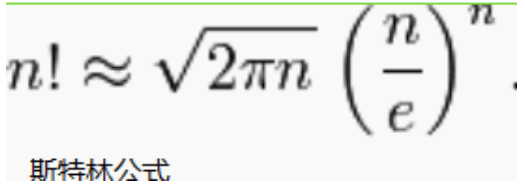
在这边 pi = acos(-1.0)  e = exp(1.0) ;

 

 int n;
    
    cin >> n;
    int len = log10(2*n*pi)/2+n*log10(n/e)+ 1;
    printf("%d\n", len);

　直接用公式就可以求得

其也可以用在求任何进制下的位数，只要将底数变成相应进制下即可，借助换底公式

 

 

扩展 ：

有一种问题是让你求 n! 末尾的 0 的个数，想这个问题，只有2和5相乘的时候才会在末尾有0出现，这里面 2 的个数又比较多，那么只需要数 5 的个数即可

int main() { 
    ll x;
    
    cin >> x;
    printf("%lld\n", x/5);    
    return 0;
}