平面最近点对

推荐博客 ： https://www.cnblogs.com/zyxStar/p/4591897.html

问题描述 ：

　　已知在平面上有散落的好多点，求相距最近的两个点的距离是多少 ？

 

一 、 穷举法

　　最暴力的解法，枚举出所有可能的点对，这样复杂度就是 n^2

 

二 、分治法  （复杂度 n*logn）

　　基本思想 ： 1 . 将原问题分解成两个或更多的问题

　　　　　　　  2 . 分解成的小问题结构是与原问题相似的

　　　　　　　  3 . 将小问题不断的分解，直到不能再分解为止，将小问题合并起来，就是原问题的答案。

 

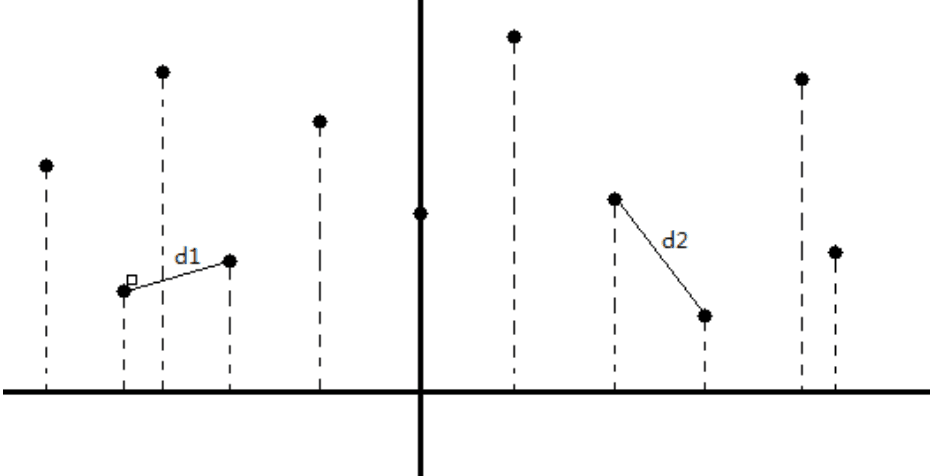
第一步我们将平面上的所有点按X轴先拍个序，从中间将这个平面一分为二，找到左半边距离最近的距离，设为 d1， 在找到右半面距离最近的距离，设为 d2 , 需要注意的是，最短距离还有可能产生在跨越中线的两侧 。d = min(d1, d2);

********************************************

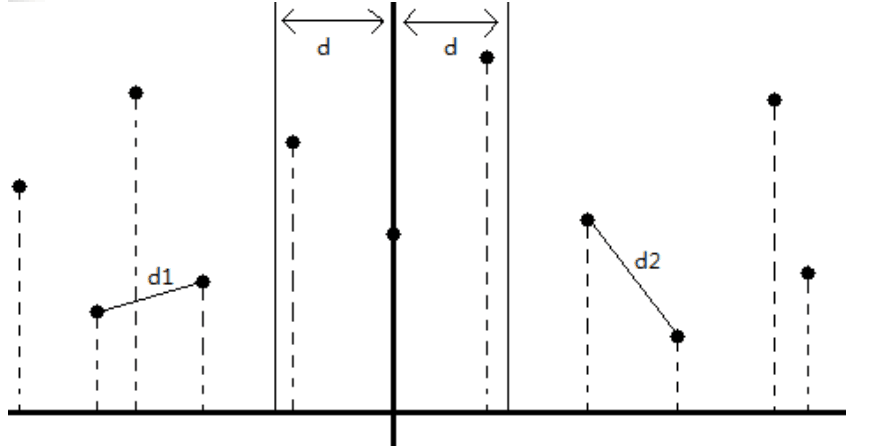
有个小剪枝的技巧是 跨中线的情况它所产生的最优解一定是在中线两侧距离为 d 的点中的组合，找到这些横坐标符合的点，对于这些点还可以再进行依次剪枝，就是对所有点的纵坐标进行一个排序，暴力的时候如果匹配点与当前的点的距离大于 d ，那么之后的点就可以直接跳过，然后在与最优解比较，并取最优的解。

struct node
{
    ll x, y;
}pre[eps], pt[eps];

bool cmpxy(node a, node b){
    if (a.x == b.y) return a.y < b.y;
    else return a.x < b.x;
}

ll dis(ll i, ll j){
    return (pre[i].x-pre[j].x)*(pre[i].x-pre[j].x)+(pre[i].y-pre[j].y)*(pre[i].y-pre[j].y);
}

ll dis2(ll i, ll j){
    return (pt[i].x-pt[j].x)*(pt[i].x-pt[j].x)+(pt[i].y-pt[j].y)*(pt[i].y-pt[j].y);
}

bool cmpy(node a, node b){
    if (a.y == b.y) return a.x < b.x;
    else return a.y < b.y;
}

ll close_pair(ll l, ll r){
    ll d = 999999999999999;
    if (l == r) return d;
    if (l + 1 == r) return dis(l, r);
    ll m = (l + r) >> 1;
    ll d1 = close_pair(l, m);
    ll d2 = close_pair(m+1, r);
    d = min(d1, d2);
    ll k = 0;
    for(ll i = l; i <= r; i++){
        if ((pre[i].x-pre[m].x)*(pre[i].x-pre[m].x) < d) pt[k++] = pre[i];
    }
    sort(pt, pt+k, cmpy);
    
    for(ll i = 0; i < k; i++){
        for(ll j = i+1; j < k && (pt[j].y-pt[i].y)*(pt[j].y-pt[i].y) < d; j++){
            ll dd = dis2(i, j);
            d = min(dd, d);
        }
    }
    return d;
}