树状数组

 推荐博客 ： https://www.cnblogs.com/RabbitHu/p/BIT.html

　　　　　　https://www.cnblogs.com/lcf-2000/p/5866170.html

树状数组的作用 ：

　　修改某点的值 ， 查询某段区间的和 ， 这是树状数组的强项 。其区间查询的和 为 lg n 。

 

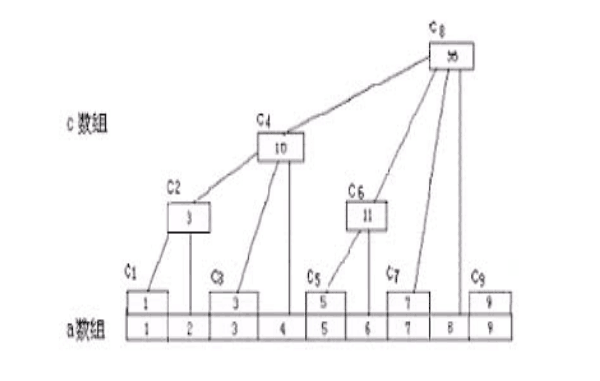
之所以叫树状数组 ， 大概就是因为他对数据的操作看起来像一颗树吧 。

 

树状数组有核心的一步 ： （追溯其父节点或下辖第一个没有关系的点）

int lowbit(int k){
    return k & (-k);
}

补充一点 ： 如何求一个负数的二进制码 ？

　　一个数加一个负号，就是把这个数的二进制码取反加一

　例如：　-10的二进制就是-1010=0101+1=0110

　然后就会发现一个规律 ： 奇数如果执行此操作 最后会返回 1 ， 但如果是偶数执行此操作 ， 得到的数是 偶数从最后一位 开始向前截取 直到有一位为 1 。

 

树状数组的更新 // 最终得到的数组是 c 数组

 

void modify(int k, int add){
    while(k <= Maxn){
        c[k] += add;
        k += lowbit(k);
    }
}

 

 

树状数组的区间求和

　　

int get_sum(int x){
    int ans = 0;
    while (x != 0){
        ans += c[x];
        x -= lowbit(x);
    }
    return ans;
}