DP -- 递推
在学习动态规划前 ， 先补充些有关递归的知识 。
所谓的递归函数 就是调用自身函数的过程 ，因此是用栈来存储的 。
递归函数的最终返回值 就是第一次调用函数的返回值 。
在写函数递归时 ， 要特别注意的两点 ：
一是 递归 递归 ， 一定有让它有能让他回归的条件 。
二是 写递归时 ， 要找到一个最简单的关系式 ， 方便写递归函数 。
递归可能出现的问题 ：
递归的特点是代码特别简洁 ， 但是也有它的缺点 。
1 . 递归是调用函数的本身 ， 所以每次调用都会有时间和空间的消耗 。而每一次调用 ， 都需要内存栈中 分配空间 ， 以保存参数 ，返回地址 ， 临时变量等参数 ，而且往栈里压入数据和弹出数据都需要时间 。
2 . 递归有很多计算都是重复的 ， 从而会对性能带来一定的负面影响 。 递归的本质是把一个问题分为两个或多个小问题 ， 如果小问题里有重叠的部分 ， 则每个重叠的部分都需要重复计算 。
3 . 除了效率外 ， 递归还存在调用栈溢出的情况 。 前面提到 每一次调用在内存中分配内存空间 ， 而每个进程的栈容量是有限的 。 当递归调用的层级太多时 ， 就会超出栈的容量 ， 从而导致栈溢出 。
话不多说 ， 进入正题 ， 先看这道题 。( poj 1163 )
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
(Figure 1)
Input
Output
Sample Input
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
Sample Output
30
题目的意思是 ： 从上到下 ，每次可以走左下角 或者右下角 ， 问最大和是多少 。
我们可以用一个二维数组去存放此三角形 。
用 pre[i][j] 表示 第 i 行 第 j 个数 ，每次移动可以有两种选择 ， 选择向左下走 ， 即 pre[i+1][j] , 或者选择向 右下走 , 即 pre[i+1][j+1] ， 若走到最后一行时 ，则返回 pre[i][j] ， 不在调用 。
下面附上我的代码 ， 还是很好理解的 ， 但 是 T 了 。
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std ;
int pre[101][101] ;
int n ;
int Max ( int i , int j ) {
if ( i == n ) return pre[i][j] ;
int x = Max ( i + 1 , j ) ;
int y = Max ( i + 1 , j + 1 ) ;
return max ( x , y ) + pre[i][j] ;
}
int main ( ) {
cin >> n ;
for ( int i = 1 ; i <= n ; i++ ) {
for ( int j = 1 ; j <= i ; j++ ) {
cin >> pre[i][j] ;
}
}
cout << Max ( 1 , 1 ) << endl ;
return 0 ;
}
想想为什么会超时 ？
这是因为 在计算时 遍历递归调用函数 ， 有一些位置的 数会计算多次 ，在本题递归时每个数递归的次数 如上图 ， 观察可知 复杂度为 2 ^ n ， 则当 n = 100 时 ， 复杂度为 2 ^ 100 ， 则会超时 。
想一个优化的办法 ， 可以在每个子节点找到它的最优路径后 ， 就记录下来 ， 此时就可以想到新建立一个数组 ， 在之前函数的基础上 ，每次返回值前先记录一次 ， 若递归调用时发现此路径之前走过 ， 则可以直接用之前的最优解 ， 这样下来会节省很多时间 。
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std ;
int pre[101][101] ;
int sum[101][101] ;
int n ;
int Max ( int i , int j ) {
if ( sum[i][j] != -1 )
return sum[i][j] ;
if ( i == n )
sum[i][j] = pre[i][j] ;
else {
int x = Max ( i + 1 , j ) ;
int y = Max ( i + 1 , j + 1 ) ;
sum[i][j] = max ( x , y ) + pre[i][j] ;
}
return sum[i][j] ;
}
int main ( ) {
cin >> n ;
for ( int i = 1 ; i <= n ; i++ ) {
for ( int j = 1 ; j <= i ; j++ ) {
cin >> pre[i][j] ;
sum[i][j] = -1 ;
}
}
cout << Max ( 1 , 1 ) << endl ;
return 0 ;
}
此时提交代码就会 AC ， 并且会发现运行时间也很短 。 但是这样的代码也是有缺陷的 ， 大量的使用堆栈空间会造成 栈溢出 ， 现在就可以考虑 将递归写成递推 。
递推的话就可以从最后一行向上推 ， 直到推到第一行 ，此时仍可以用二维数组去存每次递推的值 。
通过上述样例 ， 写出递归代码 ：
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std ;
int pre[101][101] ;
int n ;
int maxsum[101][101] ;
int main ( ) {
int i , j ;
cin >> n ;
for ( i = 1 ; i <= n ; i++ ) {
for ( j = 1 ; j <= i ; j++ ) {
cin >> pre[i][j] ;
}
}
for ( i = 1 ; i <= n ; i++ ) {
maxsum[n][i] = pre[n][i] ;
}
for ( i = n-1 ; i >= 0 ; i-- ) {
for ( j = 1 ; j <= i ; j++ ) {
maxsum[i][j] = max ( maxsum[i+1][j] , maxsum[i+1][j+1] ) + pre[i][j] ;
}
}
cout << maxsum[1][1] << endl ;
return 0 ;
}
写到这里 ， 会发现此程序仍然可以继续优化 ， 当然这个优化就是对空间的优化 ，maxsum 其实不需要用一个二维数组存 ， 一个一维数组完全可以解决问题 。
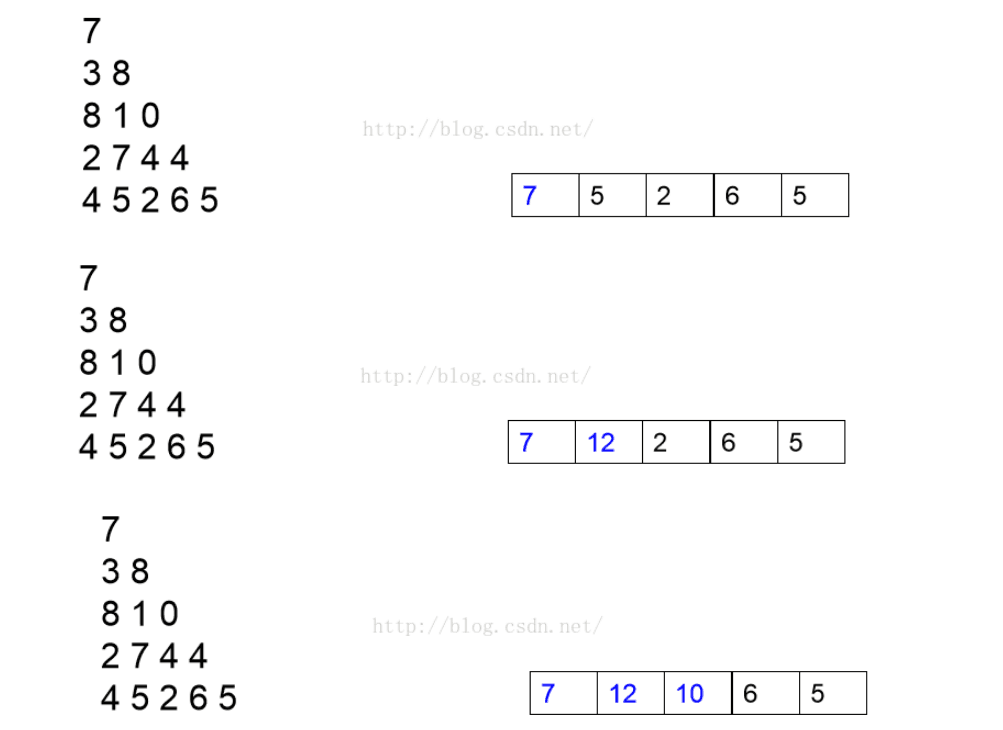
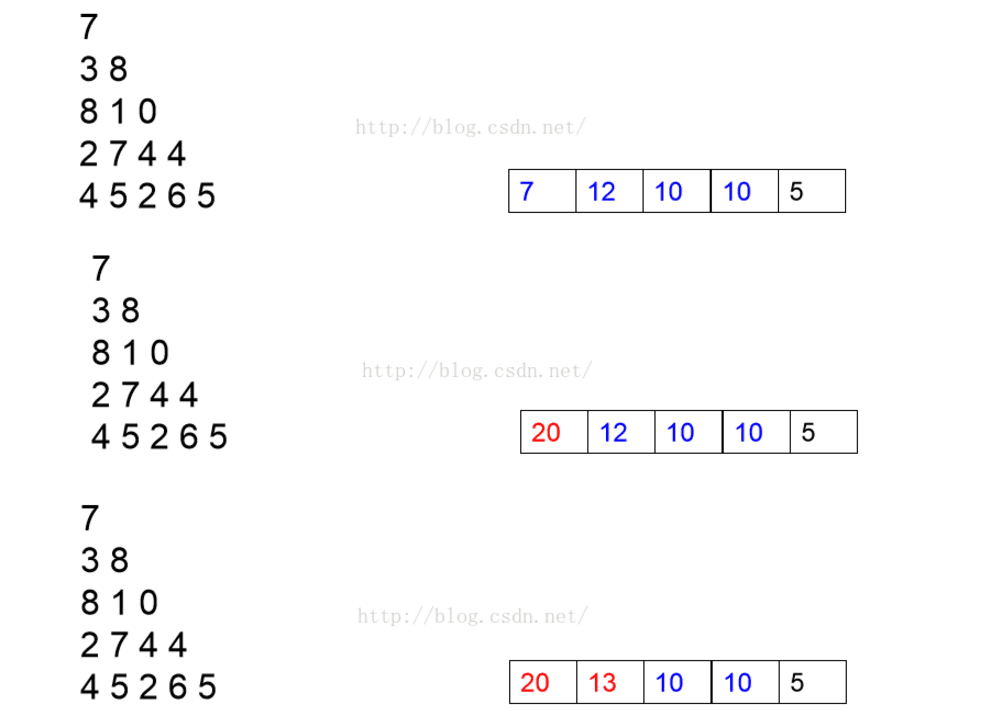
代码示例 ：
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std ;
int pre[101][101] ;
int n ;
int maxsum[101] ;
int main ( ) {
int i , j ;
cin >> n ;
for ( i = 1 ; i <= n ; i++ ) {
for ( j = 1 ; j <= i ; j++ ) {
cin >> pre[i][j] ;
}
}
for ( i = 1 ; i <= n ; i++ ) {
maxsum[i] = pre[n][i] ;
}
for ( i = n-1 ; i >= 0 ; i-- ) {
for ( j = 1 ; j <= i ; j++ ) {
maxsum[j] = max ( maxsum[j] , maxsum[j+1] ) + pre[i][j] ;
}
}
cout << maxsum[1] << endl ;
return 0 ;
}
