二分专题

 

Points in Segments

Given n points (1 dimensional) and q segments, you have to find the number of points that lie in each of the segments. A point p_i will lie in a segment A B if A ≤ p_i ≤ B.

For example if the points are 1, 4, 6, 8, 10. And the segment is 0 to 5. Then there are 2 points that lie in the segment.

Input

Input starts with an integer T (≤ 5), denoting the number of test cases.

Each case starts with a line containing two integers n (1 ≤ n ≤ 10⁵) and q (1 ≤ q ≤ 50000). The next line contains n space separated integers denoting the points in ascending order. All the integers are distinct and each of them range in [0, 10⁸].

Each of the next q lines contains two integers A_k B_k (0 ≤ A_k ≤ B_k ≤ 10⁸) denoting a segment.

Output

For each case, print the case number in a single line. Then for each segment, print the number of points that lie in that segment.

Sample Input

1

5 3

1 4 6 8 10

0 5

6 10

7 100000

Sample Output

Case 1:

2

3

2

 

题目分析 ：

　　对于刚学C++ 的我 ， 这题真的好坑我 ， 程序写的没问题 ， 就是因为输入输出的时候用的 cin , cout ，导致超时 ， 找BUG找了好长时间  。

　　

　　好了 ， 下面正式分析题目 ， 最开始看这个题就感觉是要用线段树 ， 我哪会什么线段树 ， 这题直接过 ， 后来也是听了题解才知道 ， 原来并不用线段树 ， 就是用到一个 二分找数组下标 ， 用后一个数组下标  - 前一个元素的数组下标 + 1  。

////*****/////

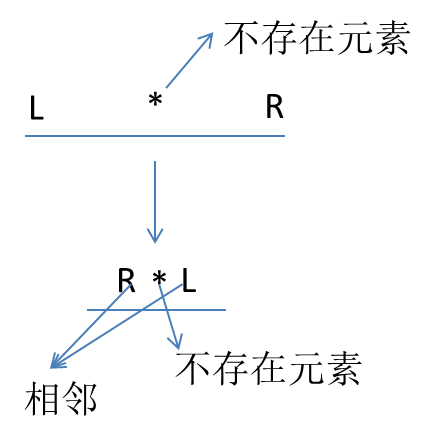
　　在二分区间找数组下标时 ， 若此元素存在 ， 直接返回数组下标 。 若此元素不存在 ，一直执行二分 ， 二分退出的条件为 Left > Right , 此时被二分的元素一定是夹在 Left 与 Right 中的 ， 所以若此元素作为待查询数据的左端临界值 ， 则返回Left , 相反则返回 Right 。

 

附图介绍下 ：

 

////*********/////

代码示例 ： 

 

#include <cstdio> 
#include <iostream>
using namespace std ;

int pre[100000] ;

int search_1 ( int key , int l , int r ) {
	int mid ;
	while ( l <= r ) {
		mid = ( l + r ) / 2 ;
		if ( pre[mid] == key ) return mid ;
		if ( pre[mid] < key ) l = mid + 1 ;
		else r = mid - 1 ; 
	}
	return l ;
}

int search_2 ( int key , int l , int r ) {
	int mid ;
	while ( l <= r ) {
		mid = ( l + r ) / 2 ;
		if ( pre[mid] == key ) return mid ;
		if ( pre[mid] < key ) l = mid + 1 ;
		else r = mid - 1 ; 
	}
	return r ;
}

int main ( ) {
	int t , n , q ;
	int x , y , k = 1 ;
	
	cin >> t ;
	while ( t-- ) {
		scanf ( "%d%d" , &n , &q ) ;
		for ( int i = 0 ; i < n ; i++ ) {
			scanf ( "%d" , &pre[i] ) ;
		}
		cout << "Case " << k++ << ':' << endl ;
		while ( q-- ) {
			scanf ( "%d%d" , &x , &y ) ;
			int a = search_1 ( x , 0 , n-1 ) , b = search_2 ( y , 0 , n - 1 ) ;
			
			printf ( "%d\n" , b -a + 1 ) ;
		}
	}
	
	return 0 ;
}

 

　　

 

 

 /////////////////////////////////////////////////////////////////////////////////

　　经过 一番讨论 ，这个题的测试样例还是有水的 ， 有一种情况没想到但是是A 了 ， 比如 在 3  3  3  中 ， 要查找的区间是  [ 0 , 2 ]  ， 若按照我的方法 ， 则返回 L = 0 ， R = -1 ; 此时就会出错 ， 所以这个题可以再最后在特判两种情况 ，带查找的两数位于 最左边 或 是待查找的两个数  位于最最右边 ， 此时特判都应该输出 0 。

 

 

////////////////////////////////////////////////////////////////////////////////////////

 

补充 一种 二分查找数组下标的方法 

　　在一个包含 N 个元素 ， 从小到大排序的 int  数组中查找比给定整数 P 小的 ， 下标最大的元素 ， 找到则返回其下标 ， 找不到则返回 - 1  。

 

代码示例 ：

　　

int searh_low ( int p ) {
	int l = 0 , r = n - 1 , mid ;
	int pt = -1 ; // 在初始时刻默认给定的最优解
	 
	while ( low <= high ) {
		mid = l + ( r - l ) / 2 ;
		if ( a[mid] >= p ) r = mid - 1 ;
		else {
			pt = mid ;
			l = mid + 1 ;
		}
	}
	
	return pt ;
}