一、题目

你将获得K个鸡蛋，并可以使用一栋从1到N共有N层楼的建筑。

每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。

你知道存在楼层F，满足0 <= F <= N任何从高于F的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。

每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层X扔下（满足 1 <= X <= N）。

你的目标是确切地知道F的值是多少。

无论F的初始值如何，你确定F的值的最小移动次数是多少？

TODO示例

二、解释

这个题目最难理解的地方就是无论F的初始值如何，这句话到底是什么意思呢？我们先放在一边:现在假设有K个鸡蛋，N层楼，当我们任选一楼X扔第一个鸡蛋，因为F不确定，此时会有两种情况鸡蛋碎了和鸡蛋没碎，当F符合碎了的情况时，继续走会有一个最终步数，当F符合第二种情况时，也会有一个最终步数

但是此时的F，你是不知道它到底是属于哪种情况，我们却得保证总能求出F的步数，所以我们只能选择max(碎了时的步数，没碎时的步数)，因为当你选择小的那个时，可能F恰好是较大那边的。

再看回题目最小移动次数该怎么保证呢？我们知道此时的X是随便选的楼，而且0<X<=N的，每个X都会有两种结果，我们都取最坏的那种，然后再取所有最坏中最小的那个，就是我们所求的，至此你应该对题目有所了解，甚至已经知道用什么方法了，下面我们将具体介绍解题方法。

三、解法

1.动态规划+二分搜索

动态规划解法大家或许已经从上面的解释中获得了灵感，那么我们一步步来完善我们的动态规划解法。

第一步：定义状态

这里我们可以定义状态dp[i][j]表示在楼层为j，鸡蛋数为i时，最少的移动次数。

  • 要注意的是这里j指的是楼层数，而不是第几楼，像[8,9,10]，j=3

第二步：推导状态转移方程

从前面的解释我们差不多知道状态转移方程是什么了，当你拥有j个鸡蛋，i层楼层时，在不知道F具体为多少的情况下，要保证确定次数最少，我们知道当我们随便选取在第X楼层扔时，会有两种情况:

  • 鸡蛋碎了，那么F肯定是在x以下的楼层中，此时楼层数就是x-1，且鸡蛋数减少为j-1，所以此时的状态为dp[x-1][j-1]。

  • 鸡蛋没碎，则F是在x以上的楼层中，楼层数为i-x，鸡蛋数不变，所以此时的状态为dp[i-x][j]。

之前我们也已经讨论如何在不知道F的情况下，求出最少步数，求在x>1&&x<=i时，每一组x取碎与不碎两种情况时的最大值，最后取所有x对应的最大值的最小值。

\[dp[i][j]=\underset{1\leq j\leq\ x}{\mathrm{min}}(1+max(dp[i-x][j],dp[x-1][j-1])) \]

当前也算走了一步，所以要加1。

第三步：考虑初始化

这也是动态规划的关键步骤，动态规划就是根据前一个状态推算下一个状态，在这里我们就可以直接写出鸡蛋数为0或1，楼层数为0或1时的情况：

  • 鸡蛋数为0时，无论楼层多少，都测不出F，所以都取0，虽然不符题意，但是会被后面状态所参考。

  • 鸡蛋数为1时，随着楼层增多而增多，第一层1次，第二层2次···

  • 楼层数为0时，也都取0

  • 楼层数为1时，无论鸡蛋有多少，都只要1次。

第四步：状态压缩

动态规划一般来说都是牺牲空间换时间，我们也可以通过状态压缩将空间尽可能也压缩，但这个题目我也没掌握，会的大佬可以教教小弟。

代码实现：

import java.util.Arrays;

public class Solution {

    public int superEggDrop(int K, int N) {

        // dp[i][j]：一共有 i 层楼梯的情况下，使用 j 个鸡蛋的最少实验的次数
        // 注意：
        // 1、i 表示的是楼层的大小，不是第几层的意思，例如楼层区间 [8, 9, 10] 的大小为 3，这一点是在状态转移的过程中调整的定义
        // 2、j 表示可以使用的鸡蛋的个数，它是约束条件，我个人习惯放在后面的维度，表示消除后效性的意思

        // 0 个楼层和 0 个鸡蛋的情况都需要算上去，虽然没有实际的意义，但是作为递推的起点，被其它状态值所参考
        int[][] dp = new int[N + 1][K + 1];

        // 由于求的是最小值，因此初始化的时候赋值为一个较大的数，9999 或者 i 都可以
        for (int i = 0; i <= N; i++) {
            Arrays.fill(dp[i], i);
        }

        // 初始化：填写下标为 0、1 的行和下标为 0、1 的列
        // 第 0 行：楼层为 0 的时候，不管鸡蛋个数多少，都测试不出鸡蛋的 F 值，故全为 0
        for (int j = 0; j <= K; j++) {
            dp[0][j] = 0;
        }

        // 第 1 行：楼层为 1 的时候，0 个鸡蛋的时候，扔 0 次，1 个以及 1 个鸡蛋以上只需要扔 1 次
        dp[1][0] = 0;
        for (int j = 1; j <= K; j++) {
            dp[1][j] = 1;
        }

        // 第 0 列：鸡蛋个数为 0 的时候，不管楼层为多少，也测试不出鸡蛋的 F 值，故全为 0
        // 第 1 列：鸡蛋个数为 1 的时候，这是一种极端情况，要试出 F 值，最少次数就等于楼层高度（想想复杂度的定义）
        for (int i = 0; i <= N; i++) {
            dp[i][0] = 0;
            dp[i][1] = i;
        }

        // 从第 2 行，第 2 列开始填表
        for (int i = 2; i <= N; i++) {
            for (int j = 2; j <= K; j++) {
                for (int k = 1; k <= i; k++) {
                    // 碎了，就需要往低层继续扔：层数少 1 ，鸡蛋也少 1
                    // 不碎，就需要往高层继续扔：层数是当前层到最高层的距离差，鸡蛋数量不少
                    // 两种情况都做了一次尝试，所以加 1
                    dp[i][j] = Math.min(dp[i][j], Math.max(dp[k - 1][j - 1], dp[i - k][j]) + 1);
                }
            }
        }
        return dp[N][K];
    }
}

这个代码最后提交会超时，我们来分析一下它的复杂度，总共有O(NK)种状态，每一种状态x都要遍历N次，所以它的时间复杂度就是O(KN^2)，空间复杂度为O(K*N)，所以我们得想办法优化一下时间，我们看到状态转移方程：

\[dp[i][j]=\underset{1\leq j\leq\ x}{\mathrm{min}}(1+max(dp[i-x][j],dp[x-1][j-1])) \]

随着层数增加，鸡蛋数不变时，dp[i][j]是单调递增的，这是显而易见的，然后看到后面两个式子dp[i-x][j]和dp[x-1][j-1]，x是在[1,x]区间内递增的，而i和j都不变，所以我们是不是可以看出dp[i-x][j]是随着x递增而单调递减，而dp[x-1][j-1]是单调递增呢？稍微思考一下就知道答案是肯定的，不过我们该如何用上这些条件呢，这就是我们下一个解法要讲到的。

动态规划+单调函数

看到公式，我们知道要求得是最大值中的最小值，也就是说要使的dp[i-x][j]和dp[x-1][j-1]的较大值尽可能的小，我们知道它们一个是递增，一个是递减的，在图上表示就是：

1.1

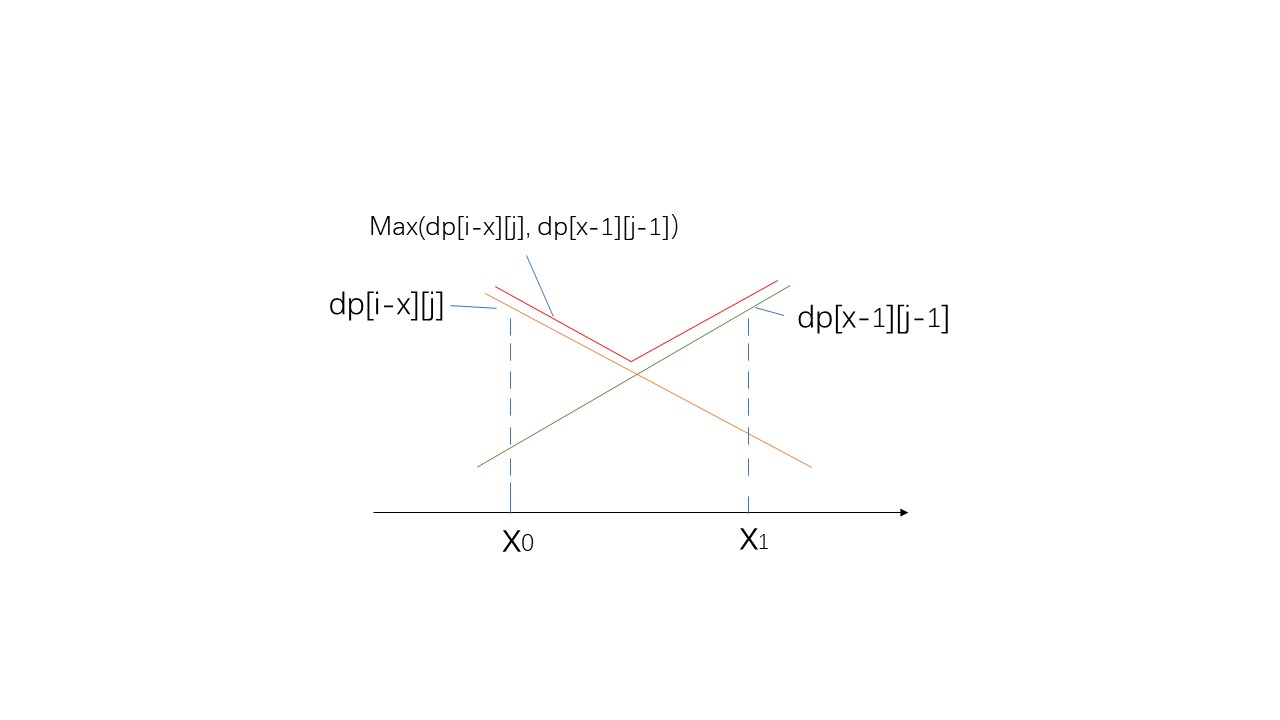
上图为了方便起见，将dp[i-x][j]和dp[x-1][j-1]都看成是连续函数，实际上它们都是离散的，也就是说x的取值只能是1,2,3···，从图中可以看出在它们相交的位置max(dp[i-x][j],dp[x-1][j-1])是最小的，但是因为这两个函数实际上是离散的，交点不一定恰好落在离散的点上，即使这样我们也知道最小值会出现在最接近交点的两个点上，而且这两点相差为1，所以我们只要找到一个x0使得dp[x0-1][j-1]<dp[i-x0][j]，并且x1=x0+1满足dp[x1-1][j-1]>=dp[i-x1][j]，这是我们就可以用到二分法了：

  • 在状态dp[i][j]上，left=1，right=i，mid=(left+right)/2。

  • 当dp[mid-1][j-1]>=dp[i-mid][j]，mid太大，rihgt=mid。

  • 当dp[mid-1][j-1]<dp[i-mid][j]，mid太小，left=mid。

  • 当left+1==right时，x0=left，x1=left+1。

最后只要求出max(dp[i-x0][j],dp[x0-1][j-1])和max(dp[i-x1][j],dp[x1-1][j-1])`较小的那个即为当前状态的最小值。

代码实现：

import java.util.Arrays;

public class Solution {

    public int superEggDrop(int K, int N) {
        // dp[i][j]：一共有 i 层楼梯的情况下，使用 j 个鸡蛋的最少仍的次数
        int[][] dp = new int[N + 1][K + 1];
        
        // 初始化
        for (int i = 0; i <= N; i++) {
            Arrays.fill(dp[i], i);
        }
        for (int j = 0; j <= K; j++) {
            dp[0][j] = 0;
        }

        dp[1][0] = 0;
        for (int j = 1; j <= K; j++) {
            dp[1][j] = 1;
        }
        for (int i = 0; i <= N; i++) {
            dp[i][0] = 0;
            dp[i][1] = i;
        }

        // 开始递推
        for (int i = 2; i <= N; i++) {
            for (int j = 2; j <= K; j++) {
                // 在区间 [1, i] 里确定一个最优值
                int left = 1;
                int right = i;
                while (left+1 < right) {
                    int mid = left + (right - left) / 2;
                    
                    int breakCount = dp[mid - 1][j - 1];
                    int notBreakCount = dp[i - mid][j];
                    if (breakCount > notBreakCount) {
                        right = mid;
                    } else if(breakCount < notBreakCount){
                        left = mid;
                    }else{
                        right=left=x;
                    }
                }
                dp[i][j] = 1+min(Math.max(dp[left - 1][j - 1], dp[i - left][j]),
                                Math.max(dp[right - 1][j - 1], dp[right - left][j]));
            }
        }
        return dp[N][K];
    }
}

时间复杂度：O(KNlogN)，二分法，对数级别的时间复杂度。
空间复杂度：O(KN)

到这里这道题目的一种解法算是结束了，果然还是写一下，理解的更透彻，虽然断断续续写了三天之久，另外如果大家还有兴趣掌握其他解法，可移步