一、字典树
字典树别名有Tire树、前缀树(prefix tree)、键树,是一种多叉树结构:
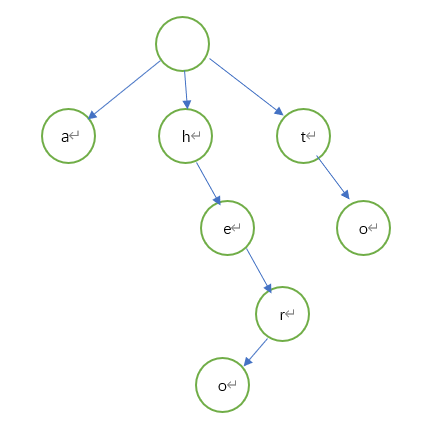
上图演示的是a、to、hero三个单词的字典树结构,从上图我们可以归纳出Trie树的基本性质:
- 根节点不包含字符,出根节点以外的每一个子节点都包含一个字符。
- 从根节点到某一个节点,路径上经过的字符连起来,为该节点所对应的字符串。
- 每个节点的所有子节点包含的字符互不相同。
由此我们得知一个字典树的节点应该包含字符和所连接子节点的指针,不过一般还要设置一个标志,用来标志该节点处是否构成一个单词:
struct trie_node{
int count;//0:不构成一个单词,>0:构成一个单词
struct trie_node *children[26]; //如上图,'to'中o对应节点的children数组值全为NULL
}
可以看出,Trie树的关键字一般都是字符串,而且Trie树把每个关键字都保存在一个路径上,而不是一个节点中。另外,有两个公共前缀的关键字,在Trie树中前缀部分路径相同。所以Trie又称为前缀树。
字典树的应用:
-
字符串检索
检索、查询功能是字典树最原始的功能之一,原理就是从根节点开始一个个字符比较
1、比较过程中字典树显示该节点为NULL,则说明该字符串在字典树中不存在。
2、比较到字符串最后一个节点时,检查当前字典树节点标识位是否标识为一个关键字。 -
词频统计
这里我们只需将count修改成一个计数器,对每一个关键字进行插入操作时,count++; -
字符串排序
我们从字典树树结构可以看出,它每一个节点数组长度都是26,当字符存在时,数组相应位置不为NULL,所以我们只需先序遍历输出Trie树中插入的所有关键字即可。 -
前缀匹配
例如:找出一个字符串集合中所有以ab开头的字符串。我们只需用所有字符串构造一个Trie树,然后输出以a->b开头的路径上的关键字即可。一般我们用的搜索引擎也体现了这种思想:

字典树例题:
一、题目:
给定一个单词列表,我们将这个列表编码成一个索引字符串 S 与一个索引列表 A。
例如,如果这个列表是 ["time", "me", "bell"],我们就可以将其表示为 S = "time#bell#" 和 indexes = [0, 2, 5]。
对于每一个索引,我们可以通过从字符串 S 中索引的位置开始读取字符串,直到 "#" 结束,来恢复我们之前的单词列表。
那么成功对给定单词列表进行编码的最小字符串长度是多少呢?
示例:
输入:words=["time","me","bell"]
输出:10
说明:S="time#bell#",indexes=[0,2,5]
提示:
- 1<=words.length<=2000
- 1<=word[i].length<=7
- 每个单词都是小写字母
思路:
这个题目读上去挺拗口的,但意思挺简单的,就是如果一个单词可以表示为另一个单词的后缀
即可看成一个单词,例如:"time"和"me",me为time的后缀,所以它们可以看出一个单词time。至此我们可以与字典树联系起来了,但有人可能会说这是后缀类型的,而字典树是判断前缀的,其实我们只需将单词逆序插入就行了。
比如题目中的 ["time","me","bell"] 的逆序就是 ["emit","em","lleb"] 。可以发现em是emit的前缀。但是我们必须先插入单词长的字符串,否则就会产生问题,这里可以阅读代码理解。所以我们插入之前需要根据单词的长度由长到短排序。
代码:
class Solution {
public int minimumLengthEncoding(String[] words) {
int len = 0;
Trie trie = new Trie();
// 先对单词列表根据单词长度由长到短排序
Arrays.sort(words, (s1, s2) -> s2.length() - s1.length());
// 单词插入trie,返回该单词增加的编码长度
for (String word: words) {
len += trie.insert(word);
}
return len;
}
}
// 定义tire
class Trie {
TrieNode root;
public Trie() {
root = new TrieNode();
}
public int insert(String word) {
TrieNode cur = root;
boolean isNew = false;
// 倒着插入单词
for (int i = word.length() - 1; i >= 0; i--) {
int c = word.charAt(i) - 'a';
if (cur.children[c] == null) {
isNew = true; // 是新单词
cur.children[c] = new TrieNode();
}
cur = cur.children[c];
}
// 如果是新单词的话编码长度增加新单词的长度+1,否则不变。
//如果是短单词先插入的话,会计算短单词的长度,后面长单词也会计算,然而短单词是
//长单词的后缀,应舍去
return isNew? word.length() + 1: 0;
}
}
class TrieNode {
char val;
TrieNode[] children = new TrieNode[26];
public TrieNode() {}
}
总结:
至此我们已经对字典树有了初步理解,一般遇到需要大量判断一个字符串是不是给点单词列表中的前缀或后缀,可以往字典树方向思考,相比于用 HashMap,节省了大量运行时间和存储空间,HashMap的效率取决于哈希函数的好坏,若一个坏的哈希函数导致了很多冲突,效率不一定比Trie树高。


