直角梯形面积公式
直角梯形面积公式
\[S_梯ABCD=\frac{x\left ( y+z \right ) }{2}
\]
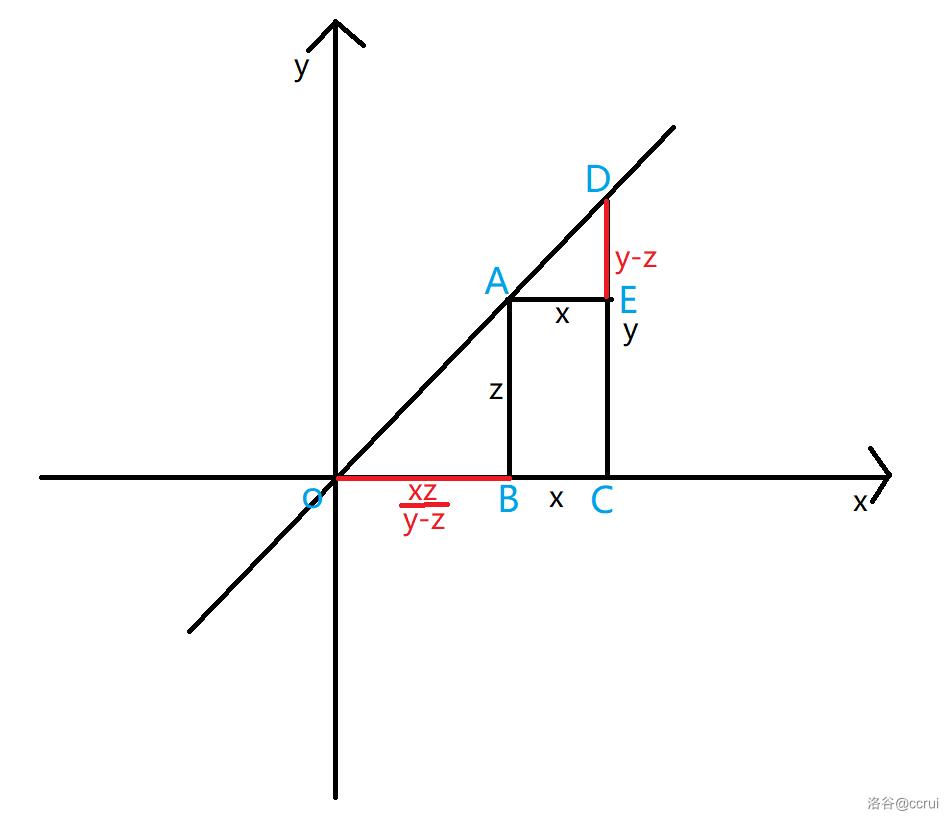
0.建系
以DA延长线与CB延长线的交点作为原点,以过点O的铅垂线作为y轴,水平线作为x轴
1.求OB
易证:\(△AOB∽△DAE\)(三垂直:\(AE⊥AB,AB⊥OB,ED⊥AE\))
所以有
\[\frac{AB}{DE} =\frac{OB}{AE}
\]
又
\[AB=z,AE=x,DE=DC-EC=DC-AB=y-z
\]
所以
\[OB=\frac{xz}{y-z}
\]
2.求直线OB的表达式
当
\[x=OB=\frac{xz}{y-z}
\]
时
\[y=z
\]
又直线OB经过原点
所以直线OB可表示为
\[y=\frac{y-z}{x} x
\]
3.积分表达式
\[{\Large \int_{\frac{xz}{y-z} }^{\frac{xz}{y-z}+x } \frac{y-z}{x} x dx }
\]
4.计算
\[\int_{\frac{xz}{y-z} }^{\frac{xz}{y-z}+x } \frac{y-z}{x} x dx
=\frac{y-z}{x} \left [ \frac{\left ( \frac{xz}{y-z}+x \right )^2 }{2}+c-\frac{\left ( \frac{xz}{y-z} \right )^2 }{2}-c \right ]
= \frac{y-z}{x}\left [ \frac{x^2}{2}+\frac{x^2z}{y-z} \right ]
=\frac{xy-xz}{2}+xz
=\frac{xy+xz}{2}
=\frac{x\left ( y+z \right ) }{2}
\]
\[\mathbf{@ccrui}\\
\mathsf{https://www.luogu.com.cn/user/664158}
\]

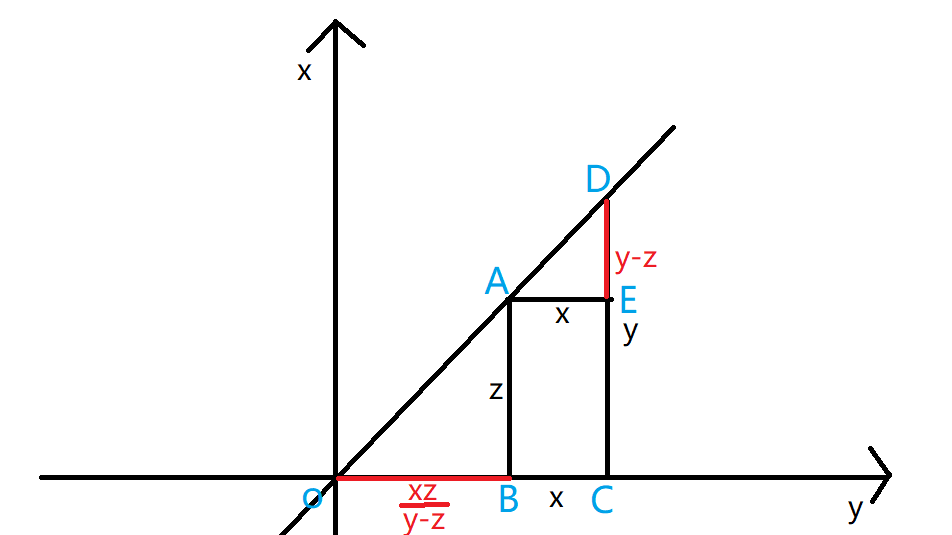 微积分证明直角梯形面积公式
微积分证明直角梯形面积公式

 浙公网安备 33010602011771号
浙公网安备 33010602011771号