【机器学习】线性回归实现与应用

文章目录

• 前置知识
• 一元线性回归
• • Step1 导入数据
  • Step2 一元函数代码实现
  • Step3 平方损失函数代码实现
  • Step4 最小二乘法代码实现
  • • • Step4.1 代数方式实现
      • Step4.2 矩阵方式实现
  • Step5 计算参数和平方损失值
  • • • Step5.1 使用代数最小二乘函数实现
      • Step5.2 使用矩阵最小二乘函数实现
• 线性回归scikit_learn实现
• 线性回归预测实战
• • 导入数据
  • 查看数据
  • 划分训练集和测试集
  • 构建和训练模型
  • 预测
  • 预测结果分析
  • • 绝对误差函数
    • 均方误差函数
    • 结果分析

前置知识

【机器学习】最小二乘法（代数&矩阵推导）

一元线性回归

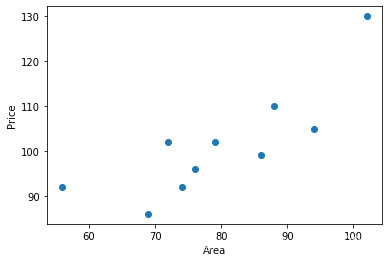
如何用一条直线拟合图中所示散点图？

Step1 导入数据

import numpy as np

x = np.array([56, 72, 69, 88, 102, 86, 76, 79, 94, 74])
y = np.array([92, 102, 86, 110, 130, 99, 96, 102, 105, 92])

Step2 一元函数代码实现

def f(x, w0, w1):
	return w0+w1*x

Step3 平方损失函数代码实现

def square_loss(x, y, w0, w1):
    loss = sum(np.square(y - (w0 + w1*x)))
    return loss

Step4 最小二乘法代码实现

Step4.1 代数方式实现

def w_calculator(x, y):
    n = len(x)
    w1 = (n*sum(x*y) - sum(x)*sum(y))/(n*sum(x*x) - sum(x)*sum(x))
    w0 = (sum(x*x)*sum(y) - sum(x)*sum(x*y))/(n*sum(x*x)-sum(x)*sum(x))
    return w0, w1

Step4.2 矩阵方式实现

def w_matrix(x, y):
    w = (x.T * x).I * x.T * y
    return w

Step5 计算参数和平方损失值

Step5.1 使用代数最小二乘函数实现

a=w_calculator(x, y)
w0 = w_calculator(x, y)[0]
w1 = w_calculator(x, y)[1]
b=square_loss(x, y, w0, w1)
print('参数：'+str(a))
print('平方损失值：'+str(b)))

Step5.2 使用矩阵最小二乘函数实现

x = np.array([56, 72, 69, 88, 102, 86, 76, 79, 94, 74])
y = np.array([92, 102, 86, 110, 130, 99, 96, 102, 105, 92])
xo=np.ones((len(x), 1))
xt=x.reshape(len(x), 1)
x=np.matrix(np.hstack((xo, xt)))
y=np.matrix(y)
w_matrix(x, y.reshape(10, 1))

若要预测x=150时，y的取值：model.predict(150， w0， w1)

线性回归scikit_learn实现

from sklearn.linear_model import LinearRegression

model=LinearRegression()
model.fit(x.reshape(len(x), 1), y)
model.intercept_, model.coef_

其中intercept_为截距项，coef_为系数项。
若要预测x=150时，y的取值：model.predict([[150]])

线性回归预测实战

波士顿房价数据集线性回归预测

导入数据

import pandas as pd
df=pd.read_csv( "https://labfile.oss.aliyuncs.com/courses/1081/course-5-boston.csv")

查看数据

describe() 统计了每列数据的个数、最大值、最小值、平均数等信息。

pf.head()
factors = df
factors.describe()

划分训练集和测试集

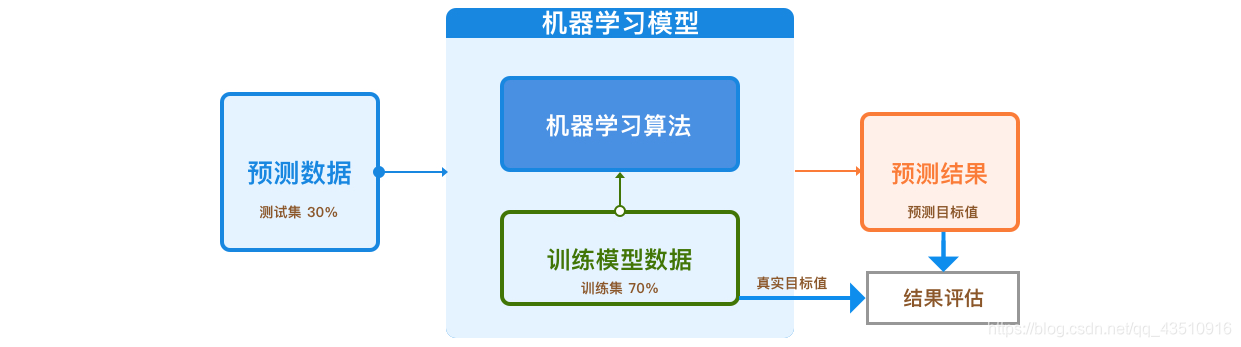
target=df['medv']
split_num=int(len(factors)*0.7)
X_train=factors[:split_num]
y_train=target[:split_num]
X_test=factors[split_num:]
y_test=target[split_num:]

构建和训练模型

model=LinearRegression()
model.fit(X_train, y_train)
model.coef_, model.intercept_

输出：

(array([-4.51975730e-15, -4.86703322e-15,  4.47479439e-16,  3.90548016e-15,
         1.45941429e-14, -3.92228185e-16, -4.37470658e-15, -6.87923840e-16,
         6.11917293e-17,  2.81345485e-16,  2.60027157e-16, -1.56843527e-16,
        -3.09108079e-16,  1.00000000e+00]),
 2.8066438062523957e-13)

预测

preds=model.predict(X_test)
preds

预测结果分析

绝对误差函数

$$\text{MAE}(y,\hat{y})=\frac{1}{n}\sum _{i=1}^n|y_i-{\hat{y}}_i|$$

def mae_value(y_true, y_prds):
    mae=sum(np.abs(y_true-y_prds))/len(y_true)
    return mae

均方误差函数

$$\text{MSE}(y,\hat{y})=\frac{1}{n}\sum _{i=1}^n(y_i-\widehat{y_i}{)}^2$$

def mse_value(y_true, y_pred):
    n = len(y_true)
    mse = sum(np.square(y_true - y_pred))/n
    return mse

结果分析

mae = mae_value(y_test.values, preds)
mse = mse_value(y_test.values, preds)
print("MAE: ", mae)
print("MSE: ", mse)

输出：

MAE:  6.844817110767938e-14
MSE:  8.884722400780445e-27