【机器学习】多项式回归

文章目录

多项式回归介绍
多项式回归基础
多项式回归预测

多项式回归介绍

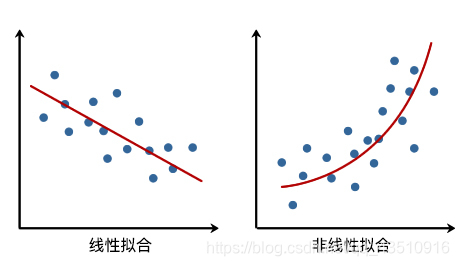
前面我们拟合直线用到了线性回归，而非线性回归中，则需要建立因变量和自变量之间的非线性关系。从直观上讲，也就是拟合的直线变成了「曲线」。
在这里插入图片描述

多项式回归基础

导入数据
x = [4, 8, 12, 25, 32, 43, 58, 63, 69, 79]
y = [20, 33, 50, 56, 42, 31, 33, 46, 65, 75]

实现二次多项式拟合

$w_0 + w_1x + w_2x^2 +...+w_mx^m = \sum\limits_{j=0}^{m}w_jx^j$ 其中， $m$ 表示多项式的阶数， $x^j$ 表示 $x$ 的 $j$ 次幂， $w$ 则代表该多项式的系数。
这里首先指定 𝑚=2，多项式就变成了:
$w_0 + w_1x + w_2x^2= \sum\limits_{j=0}^{2}w_jx^j$

def func(p, x):
    # 根据公式，定义 2 次多项式函数
    w0, w1, w2 = p
    f = w0 + w1*x + w2*x*x
    return f


def err_func(p, x, y):
    # 残差函数（观测值与拟合值之间的差距）
    ret = func(p, x) - y
    return ret

接下来，就是使用最小二乘法求解最优参数的过程。这里为了方便，我们直接使用 Scipy 提供的最小二乘法类，得到最佳拟合参数。当然，你完全可以按照线性回归实验中最小二乘法公式自行求解参数。不过，实际工作中为了快速实现，往往会使用像 Scipy 这样现成的函数。

import numpy as np
from scipy.optimize import leastsq

p_init = np.random.randn(3)  # 生成 3 个随机数
# 使用 Scipy 提供的最小二乘法函数得到最佳拟合参数
parameters = leastsq(err_func, p_init, args=(np.array(x), np.array(y)))

print('Fitting Parameters: ', parameters[0])

输出：Fitting Parameters: [ 3.76893104e+01 -2.60474036e-01 8.00077945e-03]
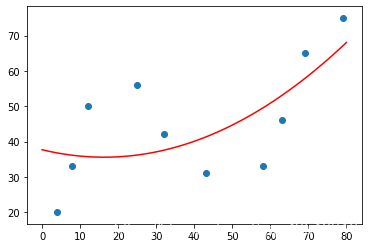
所以拟合出的图像为： $0.0080x^2 \tag{3}$

在这里插入图片描述

实现N次多项式拟合

def fit_func(p, x):
    """根据公式，定义 n 次多项式函数
    """
    f = np.poly1d(p)
    return f(x)


def err_func(p, x, y):
    """残差函数（观测值与拟合值之间的差距）
    """
    ret = fit_func(p, x) - y
    return ret


def n_poly(n):
    """n 次多项式拟合
    """
    p_init = np.random.randn(n)  # 生成 n 个随机数
    parameters = leastsq(err_func, p_init, args=(np.array(x), np.array(y)))
    return parameters[0]

使用 scikit-learn 进行多项式拟合

对于一个二次多项式而言，我们知道它的标准形式为： $y(x, w) = w_0 + w_1x + w_2x^2$ 。但是，多项式回归却相当于线性回归的特殊形式。例如，我们这里令 $x = x_1$ , $x^2 = x_2$ ，那么原方程就转换为： $y(x, w) = w_0 + w_1x_1 + w_2x_2$ ，这也就变成了多元线性回归。这就完成了一元高次多项式到多元一次多项式之间的转换。这就类似于高中数学学习过的「换元法」。
举例说明，对于自变量向量 $X$ 和因变量 $y$ ，如果 $X$ ：
$X=\left[ \begin{array}{c}{2} \\ {-1} \\ {3}\end{array}\right]$

我们可以通过 $y = w_1 x + w_0$ 线性回归模型进行拟合。同样，如果对于一元二次多项式 $y(x, w) = w_0 + w_1x + w_2x^2$ ，如果能得到由 $x = x_1$ , $x^2 = x_2$ 构成的特征矩阵，即：
$X=\left[X, X^{2}\right]=\left[ \begin{array}{cc}{2} & {4} \\ {-1} & {1} \\ {3} & {9}\end{array}\right]$

在 scikit-learn 中，我们可以通过 PolynomialFeatures() 类自动产生多项式特征矩阵，PolynomialFeatures() 类的默认参数及常用参数定义如下：

sklearn.preprocessing.PolynomialFeatures(degree=2,
interaction_only=False, include_bias=True)

degree: 多项式次数，默认为 2 次多项式
interaction_only: 默认为 False，如果为 True 则产生相互影响的特征集。
include_bias: 默认为 True，包含多项式中的截距项。

对应上面的特征向量，我们使用 PolynomialFeatures() 的主要作用是产生 2 次多项式对应的特征矩阵，如下所示：

from sklearn.preprocessing import PolynomialFeatures
X = [2, -1, 3]
X_reshape = np.array(X).reshape(len(X), 1)  # 转换为列向量
# 使用 PolynomialFeatures 自动生成特征矩阵
PolynomialFeatures(degree=2, include_bias=False).fit_transform(X_reshape)

输出：

array([[ 2.,  4.],
       [-1.,  1.],
       [ 3.,  9.]])

使用之前的数据：
先产生特征矩阵：

x = np.array(x).reshape(len(x), 1)  # 转换为列向量
y = np.array(y).reshape(len(y), 1)

# 使用 sklearn 得到 2 次多项式回归特征矩阵
poly_features = PolynomialFeatures(degree=2, include_bias=False)
poly_x = poly_features.fit_transform(x)

再使用特征矩阵训练模型：

from sklearn.linear_model import LinearRegression

# 定义线性回归模型
model = LinearRegression()
model.fit(poly_x, y)  # 训练

# 得到模型拟合参数
model.intercept_, model.coef_

多项式回归预测

导入数据集

import pandas as pd
df=pd.read_csv( "https://labfile.oss.aliyuncs.com/courses/1081/course-6-vaccine.csv", header=0)
df

绘制图表查看变化趋势

plt.plot(df['Year'],df['Values'], 'r')
plt.scatter(df['Year'],df['Values'])

线性回归与 2 次多项式回归对比

线性回归

划分数据集

# 首先划分 dateframe 为训练集和测试集
train_df = df[:int(len(df)*0.7)]
test_df = df[int(len(df)*0.7):]

# 定义训练和测试使用的自变量和因变量
X_train = train_df['Year'].values
y_train = train_df['Values'].values

X_test = test_df['Year'].values
y_test = test_df['Values'].values

训练模型并预测

# 建立线性回归模型
model = LinearRegression()
model.fit(X_train.reshape(len(X_train), 1), y_train.reshape(len(y_train), 1))
results = model.predict(X_test.reshape(len(X_test), 1))
results  # 线性回归模型在测试集上的预测结果

预测结果分析

平均绝对误差（MAE）就是绝对误差的平均值

$\textrm{MAE}(y, \hat{y} ) = \frac{1}{n}\sum_{i=1}^{n}{|y_{i}-\hat y_{i}|}$

均方误差（MSE）它表示误差的平方的期望值
$\textrm{MSE}(y, \hat{y} ) = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y})^{2}$

flatten()函数表示返回一个一维数组

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error

print("线性回归平均绝对误差: ", mean_absolute_error(y_test, results.flatten()))
print("线性回归均方误差: ", mean_squared_error(y_test, results.flatten()))

输出：
线性回归平均绝对误差: 6.011979515629853 线性回归均方误差: 43.53185829515393

2次多项式回归

# 2 次多项式回归特征矩阵
poly_features_2 = PolynomialFeatures(degree=2, include_bias=False)
poly_X_train_2 = poly_features_2.fit_transform(
    X_train.reshape(len(X_train), 1))
poly_X_test_2 = poly_features_2.fit_transform(X_test.reshape(len(X_test), 1))

# 2 次多项式回归模型训练与预测
model = LinearRegression()
model.fit(poly_X_train_2, y_train.reshape(len(X_train), 1))  # 训练模型

results_2 = model.predict(poly_X_test_2)  # 预测结果

#results_2.flatten()  # 打印扁平化后的预测结果
print("2 次多项式回归平均绝对误差: ", mean_absolute_error(y_test, results_2.flatten()))
print("2 次多项式均方误差: ", mean_squared_error(y_test, results_2.flatten()))

输出： 2 次多项式回归平均绝对误差: 19.792070829567653 2 次多项式均方误差: 464.3290384751541

根据上面平均绝对误差和均方误差的定义，你已经知道这两个取值越小，代表模型的预测准确度越高。也就是说，线性回归模型的预测结果要优于 2 次多项式回归模型的预测结果。

更高次多项式回归预测

这里将通过实例化 make_pipeline 管道类，实现调用一次 fit 和 predict 方法即可应用于所有预测器。make_pipeline 是使用 sklearn 过程中的技巧创新，其可以将一个处理流程封装起来使用。

from sklearn.pipeline import make_pipeline

X_train = X_train.reshape(len(X_train), 1)
X_test = X_test.reshape(len(X_test), 1)
y_train = y_train.reshape(len(y_train), 1)

for m in [3, 4, 5]:
    model = make_pipeline(PolynomialFeatures(
        m, include_bias=False), LinearRegression())
    model.fit(X_train, y_train)
    pre_y = model.predict(X_test)
    print("{} 次多项式回归平均绝对误差: ".format(m),
          mean_absolute_error(y_test, pre_y.flatten()))
    print("{} 次多项式均方误差: ".format(m), mean_squared_error(y_test, pre_y.flatten()))

输出：
3 次多项式回归平均绝对误差: 4.5476919429640335
3 次多项式均方误差: 29.933056670525307

4 次多项式回归平均绝对误差: 4.424336223586132
4 次多项式均方误差: 29.02874897635671

5 次多项式回归平均绝对误差: 4.341616358034744
5 次多项式均方误差: 28.221927580869462

多项式回归预测次数选择

# 计算 m 次多项式回归预测结果的 MSE 评价指标并绘图
mse = []  # 用于存储各最高次多项式 MSE 值
m = 1  # 初始 m 值
m_max = 10  # 设定最高次数
while m <= m_max:
    model = make_pipeline(PolynomialFeatures(
        m, include_bias=False), LinearRegression())
    model.fit(X_train, y_train)  # 训练模型
    pre_y = model.predict(X_test)  # 测试模型
    mse.append(mean_squared_error(y_test, pre_y.flatten()))  # 计算 MSE
    m = m + 1

print("MSE 计算结果: ", mse)
# 绘图
plt.plot([i for i in range(1, m_max + 1)], mse, 'r')
plt.scatter([i for i in range(1, m_max + 1)], mse)

# 绘制图名称等
plt.title("MSE of m degree of polynomial regression")
plt.xlabel("m")
plt.ylabel("MSE")

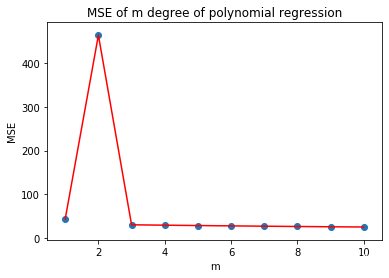
在这里插入图片描述
如上图所示，MSE 值在 2 次多项式回归预测时达到最高点，之后迅速下降。而 3 次之后的结果虽然依旧呈现逐步下降的趋势，但趋于平稳。一般情况下，我们考虑到模型的泛化能力，避免出现过拟合，这里就可以选择 3 次多项式为最优回归预测模型。

posted @ 2020-09-07 16:19 ccql 阅读(74) 评论(0) 编辑收藏举报来源

刷新页面返回顶部

ccql