【机器学习】岭回归和 LASSO 回归实现
普通最小二乘法的缺陷
普通最小二乘法带来的局限性，导致许多时候都不能直接使用其进行线性回归拟合。特别是以下两种情况：
- 数据集的列（特征）数量 > 数据量（行数量），即 X X X不是列满秩。
- 数据集列（特征）数据之间存在较强的线性相关性，即模型容易出现过拟合。
岭回归推导
为了解决上述两种情况中出现的问题，岭回归（Ridge Regression）应运而生。岭回归可以被看作为一种改良后的最小二乘估计法，它通过向损失函数中添加
L
2
L2
L2正则项（2-范数）有效防止模型出现过拟合，且以助于解决非满秩条件下求逆困难的问题，从而提升模型的解释能力。即
对应的损失函数由：
F
n
o
r
m
a
l
=
∑
i
=
1
n
(
y
i
−
w
T
x
)
2
F_{normal}=\sum_{i=1}^{n}(y_{i}-w^Tx)^2
Fnormal=i=1∑n(yi−wTx)2
变为：
F
R
i
d
g
e
=
∑
i
=
1
n
(
y
i
−
w
T
x
)
2
+
λ
∑
i
=
1
n
(
w
i
)
2
F_{Ridge}=\sum_{i=1}^{n}(y_{i}-w^Tx)^2 + \lambda \sum_{i=1}^{n}(w_{i})^2
FRidge=i=1∑n(yi−wTx)2+λi=1∑n(wi)2
我们可以把公式改写为向量表示：
F Ridge = ∥ y − X w ∥ 2 2 + λ ∥ w ∥ 2 2 F_{\text {Ridge}}=\|y-X w\|_{2}^{2}+\lambda\|w\|_{2}^{2} FRidge=∥y−Xw∥22+λ∥w∥22
公式中回归系数 w w w的解析解为：
w ^ R i d g e = ( X T X + λ I ) − 1 X T Y \hat w_{Ridge} = (X^TX + \lambda I)^{-1} X^TY w^Ridge=(XTX+λI)−1XTY
从公式的区别可以看出，通过给 X T X XTX XTX增加一个单位矩阵，从而使得矩阵变成满秩，完善普通最小二乘法的不足。
岭回归拟合
sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto', random_state=None)
alpha: 正则化强度，默认为 1.0，对应公式 8 中的 λ \lambda λ。fit_intercept: 默认为 True，计算截距项。normalize: 默认为 False，不针对数据进行标准化处理。copy_X: 默认为 True，即使用数据的副本进行操作，防止影响原数据。max_iter: 最大迭代次数，默认为 None。tol: 数据解算精度。solver: 根据数据类型自动选择求解器。random_state: 随机数发生器。
from sklearn.linear_model import Ridge
ridge_model = Ridge(fit_intercept=False) # 参数代表不增加截距项
ridge_model.fit(x, y)
ridge_model.coef_ # 打印模型参数
LASSO回归
sklearn.linear_model.Lasso(alpha=1.0, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='cyclic')
- alpha: 正则化强度，默认为 1.0。
- fit_intercept: 默认为 True，计算截距项。
- normalize: 默认为 False，不针对数据进行标准化处理。
- precompute: 是否使用预先计算的 Gram 矩阵来加速计算。
- copy_X: 默认为 True，即使用数据的副本进行操作，防止影响原数据。
- max_iter: 最大迭代次数，默认为 1000。
- tol: 数据解算精度。
- warm_start: 重用先前调用的解决方案以适合初始化。
- positive: 强制系数为正值。
- random_state: 随机数发生器。
- selection: 每次迭代都会更新一个随机系数。
"""
使用 LASSO 回归拟合并绘图
"""
from sklearn.linear_model import Lasso
alphas = np.linspace(-2,2,10)
lasso_coefs = []
for a in alphas:
lasso = Lasso(alpha=a, fit_intercept=False)
lasso.fit(x, y)
lasso_coefs.append(lasso.coef_)
plt.plot(alphas, lasso_coefs) # 绘制不同 alpha 参数下的 w 拟合值
plt.scatter(np.linspace(0,0,10), parameters[0]) # 普通最小二乘法拟合的 w 值放入图中
plt.xlabel('alpha')
plt.ylabel('w')
plt.title('Lasso Regression')
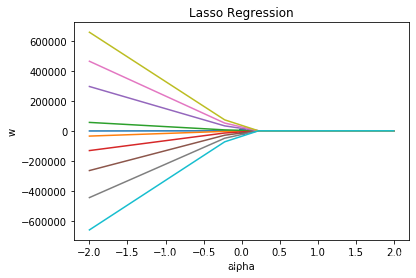
由图可见，当 alpha 取值越大时，正则项主导收敛过程，各 𝑤 系数趋近于 0。当 alpha 很小时，各 𝑤 系数波动幅度变大。
