【机器学习】回归方法综合应用练习

文章目录

• 一元线性回归模型
• • 加载数据集
  • 计算拟合参数
  • 拟合结果绘图
• 多元线性回归模型
• • 计算拟合参数
• 模型检验

一元线性回归模型

使用 SciPy 提供的普通最小二乘法分别计算 3 个特征与目标之间的一元线性回归模型拟合参数。

加载数据集

import pandas as pd

data = pd.read_csv(
    'http://labfile.oss.aliyuncs.com/courses/1211/Advertising.csv', index_col=0)
data.head()

数据集包含 4 列，共 200 行。每个样本代表某超市销售相应单位件商品所需要支出的广告费用。以第一行为例，表示该超市平均销售 22.1 件商品，需要支出的电视广告费用，广播广告费用以及报刊广告费用为：230.1 美元，37.8 美元和 69.2 美元。将前 3 列视作特征，最后一列视作目标值。

计算拟合参数

import numpy as np
from scipy.optimize import leastsq

### 代码开始 ### (≈ 10 行代码)
m=2
def func(w, x):
    return w[0]+w[1]*x
def err_func(w, x, y):
    return y-func(w, x)
params_tv = leastsq(err_func,[1, 1], args=(data['tv'], data['sales']))
params_radio = leastsq(err_func,[1, 1], args=(data['radio'], data['sales']))
params_newspaper = leastsq(err_func,[1, 1], args=(data['newspaper'], data['sales']))
### 代码结束 ###

params_tv[0], params_radio[0], params_newspaper[0]

输出：
(array([7.03259358, 0.04753664]), array([9.3116381 ,
0.20249578]), array([12.35140707, 0.0546931 ]))

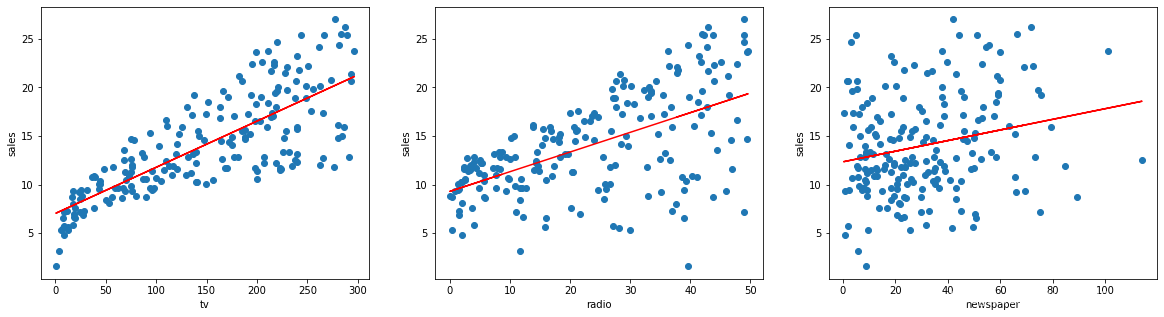
拟合结果绘图

from matplotlib import pyplot as plt
%matplotlib inline

### 代码开始 ### (≈ 10 行代码)
fig, axes=plt.subplots(1, 3, figsize=(20,5))
axes[0].scatter(data['tv'], data['sales'])
axes[0].plot(data['tv'], func(params_tv[0], data['tv']), color='red')
axes[0].set_xlabel('tv')
axes[0].set_ylabel('sales')
axes[1].scatter(data['radio'], data['sales'])
axes[1].plot(data['radio'], func(params_radio[0], data['radio']), color='red')
axes[1].set_xlabel('radio')
axes[1].set_ylabel('sales')
axes[2].scatter(data['newspaper'], data['sales'])
axes[2].plot(data['newspaper'], func(params_newspaper[0], data['newspaper']), color='red')
axes[2].set_xlabel('newspaper')
axes[2].set_ylabel('sales')
### 代码结束 ###

多元线性回归模型

使用 scikit-learn 提供的线性回归方法建立由 3 个特征与目标组成的多元线性回归模型。

计算拟合参数

from sklearn.linear_model import LinearRegression

### 代码开始 ### (≈ 4 行代码)
model = LinearRegression()
model.fit(data[['tv', 'radio', 'newspaper']], data['sales'])
### 代码结束 ###

model.coef_, model.intercept_  # 返回模型自变量系数和截距项

输出： (array([ 0.04576465, 0.18853002, -0.00103749]),
2.9388893694594103)

模型检验

使用 statsmodels 库提供的相关方法来完成上面多元回归模型的拟合优度检验和变量显著性检验。

import statsmodels.api as sm
x=sm.add_constant(data[['tv', 'radio', 'newspaper']])
model=sm.OLS(endog=data['sales'], exog=x)
results=model.fit()
### 代码结束 ###

results.summary2() # 输出模型摘要

输出：

Model: OLS	Adj. R-squared: 0.896
Dependent Variable: sales	AIC: 780.3622
Date: 2020-09-09 11:50	BIC: 793.5555
No. Observations: 200	Log-Likelihood: -386.18
Df Model: 3	F-statistic: 570.3
Df Residuals: 196	Prob (F-statistic): 1.58e-96
R-squared: 0.897	Scale: 2.8409

	Coef.	Std.Err.	t	$P>|t|$	[0.025	0.975]
const	2.9389	0.3119	9.4223	0.0000	2.3238	3.5540
tv	0.0458	0.0014	32.8086	0.0000	0.0430	0.0485
radio	0.1885	0.0086	21.8935	0.0000	0.1715	0.2055
newspaper	-0.0010	0.0059	-0.1767	0.8599	-0.0126	0.0105

Omnibus: 60.414	Durbin-Watson: 2.084
Prob(Omnibus): 0.000	Jarque-Bera (JB): 151.241
Skew: -1.327	Prob(JB): 0.000
Kurtosis: 6.332	Condition No.: 454

我们可以看到，这里得到的回归拟合系数和上文 scikit-learn 计算结果一致。于此同时，tv 和 radio 的 P 值接近于 0 [精度]，而 newspaper 的 P 值相对较大。我们可以认为 tv 和 radio 通过了变量显著性检验，而 newspaper 则未通过。