【kaggle-Top方案解析】房价预测数据探索（Comprehensive data exploration with Python by Pedro Marcelino）

本篇博客主要解读Comprehensive data exploration with Python by Pedro Marcelino数据处理方案

文章目录

• 0. 导入库
• 1. 一些关于特征的思考
• 2. 分析`SalePrice`以及与其相关单变量的关系
• • 2.1 分析`SalePrice`特征
  • 2.2 分析与相关单变量之间的关系
  • • 2.2.1 分析数值型特征
    • • 2.2.1.1 探究与`GrLivArea`之间的关系
    • 2.2.1.2 探究与`TotalBsmtSF`之间的关系
  • 2.2.2 分析类别型数据
  • • 2.2.2.1 探究与`OverallQual`之间的关系
    • 2.2.2.2 探究与`YearBuilt`之间的关系
• 3. 使用热力图客观分析各个变量之间的关系
• 4. 缺失值处理
• • 4.1 缺失数据统计
  • 4.2 缺失数据处理
• 5. 离群值去除
• • 5.1 单变量分析
  • 5.2 多变量分析
• 6. 检验正态分布
• • 6.1 检验`SalePrice`的正态性
  • 6.2 检验`GrLivArea`的正态性
  • 6.3 检验`TotalBsmtSF`的正态性
• 7. 检验同方差性
• • 7.1 检验`SalePrice`和`GrLivArea`的同方差性
  • 7.2 检验`SalePrice`和`TotalBsmtSF`的同方差性
• 8. 特征提取

0. 导入库

# Comprehensive data exploration with Python by Pedro Marcelino
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from scipy.stats import norm
from sklearn.preprocessing import StandardScaler
from scipy import stats
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline

# You can write up to 20GB to the current directory (/kaggle/working/) that gets preserved as output when you create a version using "Save & Run All" 
# You can also write temporary files to /kaggle/temp/, but they won't be saved outside of the current session

#训练数据集导入
df_train = pd.read_csv('../input/train.csv')

#特征查看
df_train.columns

Index([‘Id’, ‘MSSubClass’, ‘MSZoning’, ‘LotFrontage’, ‘LotArea’, ‘Street’,
‘Alley’, ‘LotShape’, ‘LandContour’, ‘Utilities’, ‘LotConfig’,
‘LandSlope’, ‘Neighborhood’, ‘Condition1’, ‘Condition2’, ‘BldgType’,
‘HouseStyle’, ‘OverallQual’, ‘OverallCond’, ‘YearBuilt’, ‘YearRemodAdd’,
‘RoofStyle’, ‘RoofMatl’, ‘Exterior1st’, ‘Exterior2nd’, ‘MasVnrType’,
‘MasVnrArea’, ‘ExterQual’, ‘ExterCond’, ‘Foundation’, ‘BsmtQual’,
‘BsmtCond’, ‘BsmtExposure’, ‘BsmtFinType1’, ‘BsmtFinSF1’,
‘BsmtFinType2’, ‘BsmtFinSF2’, ‘BsmtUnfSF’, ‘TotalBsmtSF’, ‘Heating’,
‘HeatingQC’, ‘CentralAir’, ‘Electrical’, ‘1stFlrSF’, ‘2ndFlrSF’,
‘LowQualFinSF’, ‘GrLivArea’, ‘BsmtFullBath’, ‘BsmtHalfBath’, ‘FullBath’,
‘HalfBath’, ‘BedroomAbvGr’, ‘KitchenAbvGr’, ‘KitchenQual’,
‘TotRmsAbvGrd’, ‘Functional’, ‘Fireplaces’, ‘FireplaceQu’, ‘GarageType’,
‘GarageYrBlt’, ‘GarageFinish’, ‘GarageCars’, ‘GarageArea’, ‘GarageQual’,
‘GarageCond’, ‘PavedDrive’, ‘WoodDeckSF’, ‘OpenPorchSF’,
‘EnclosedPorch’, ‘3SsnPorch’, ‘ScreenPorch’, ‘PoolArea’, ‘PoolQC’,
‘Fence’, ‘MiscFeature’, ‘MiscVal’, ‘MoSold’, ‘YrSold’, ‘SaleType’,
‘SaleCondition’, ‘SalePrice’],
dtype=‘object’)

1. 一些关于特征的思考

（思考方法，值得一看）

如下引用一部分原文(下面有翻译)：

In order to understand our data, we can look at each variable and try to understand their meaning and relevance to this problem. I know this is time-consuming, but it will give us the flavour of our dataset.
In order to have some discipline in our analysis, we can create an Excel spreadsheet with the following columns:
 Variable - Variable name.
 Type - Identification of the variables’ type. There are two possible values for this field: ‘numerical’ or ‘categorical’. By ‘numerical’ we mean variables for which the values are numbers, and by ‘categorical’ we mean variables for which the values are categories.
 Segment - Identification of the variables’ segment. We can define three possible segments: building, space or location. When we say ‘building’, we mean a variable that relates to the physical characteristics of the building (e.g. ‘OverallQual’). When we say ‘space’, we mean a variable that reports space properties of the house (e.g. ‘TotalBsmtSF’). Finally, when we say a ‘location’, we mean a variable that gives information about the place where the house is located (e.g. ‘Neighborhood’).
 Expectation - Our expectation about the variable influence in ‘SalePrice’. We can use a categorical scale with ‘High’, ‘Medium’ and ‘Low’ as possible values.
 Conclusion - Our conclusions about the importance of the variable, after we give a quick look at the data. We can keep with the same categorical scale as in ‘Expectation’.
 Comments - Any general comments that occured to us.
While ‘Type’ and ‘Segment’ is just for possible future reference, the column ‘Expectation’ is important because it will help us develop a ‘sixth sense’. To fill this column, we should read the description of all the variables and, one by one, ask ourselves:
 Do we think about this variable when we are buying a house? (e.g. When we think about the house of our dreams, do we care about its ‘Masonry veneer type’?).
 If so, how important would this variable be? (e.g. What is the impact of having ‘Excellent’ material on the exterior instead of ‘Poor’? And of having ‘Excellent’ instead of ‘Good’?).
 Is this information already described in any other variable? (e.g. If ‘LandContour’ gives the flatness of the property, do we really need to know the ‘LandSlope’?).
After this daunting exercise, we can filter the spreadsheet and look carefully to the variables with ‘High’ ‘Expectation’. Then, we can rush into some scatter plots between those variables and ‘SalePrice’, filling in the ‘Conclusion’ column which is just the correction of our expectations.

翻译：
  为了理解我们的数据，我们可以查看每个变量，并试图了解它们的含义和与这个问题的相关性。我知道这很费时，但它会给我们的数据集的味道。
为了在我们的分析中有一些原则，我们可以创建一个包含以下列的Excel电子表格：

• Variable—变量名。
• 类型-变量类型的标识。此字段有两个可能的值：“数值”或“分类”。“数值”是指数值为数字的变量，而“分类”是指数值为类别的变量。
• 段-识别变量的段。我们可以定义三个可能的部分：建筑、空间或位置。当我们说“建筑物”时，我们指的是一个与建筑物的物理特性有关的变量（例如“总体质量”）。当我们说“space”时，我们指的是一个报告房屋空间属性的变量（例如“TotalBsmtSF”）。最后，当我们说“位置”时，我们指的是一个变量，它给出了房子所在位置的信息（例如“邻居”）。
• 期望-我们对“销售价格”中变量影响的期望。我们可以使用“高”、“中”和“低”作为可能值的分类量表。
• 结论-在我们快速查看数据之后，我们对变量重要性的结论。我们可以保持与“期望”相同的范畴尺度。
• 评论-我们遇到的任何一般性评论。

虽然“类型”和“片段”只是供将来参考，但“期望”一栏很重要，因为它将帮助我们培养“第六感”。为了填写本栏，我们应该阅读所有变量的描述，并逐一询问自己：

• 我们在买房的时候会考虑这个变量吗？（例如，当我们想到我们梦想中的房子时，我们是否关心它的‘砖石饰面类型’？）。
• 如果是，这个变量有多重要？（例如，在外观上使用“优秀”材料而不是“差”材料会产生什么影响？而不是“优秀”而不是“优秀”？）。
• 这个信息已经在其他变量中描述过了吗？（例如，如果“LandContour”给出了物业的平面度，我们真的需要知道“LandSlope”吗？）。

在这个令人生畏的练习之后，我们可以过滤电子表格并仔细查看具有“高”期望值的变量。然后，我们可以在这些变量和‘SalePrice’之间画一些散点图，填写‘结论’栏，这只是对我们预期的修正。

2. 分析SalePrice以及与其相关单变量的关系

此部分分析的相关单变量均为使用第一部分的方法主观得出。

2.1 分析SalePrice特征

#售价细节展示
df_train['SalePrice'].describe()

count 1460.000000
mean 180921.195890
std 79442.502883
min 34900.000000
25% 129975.000000
50% 163000.000000
75% 214000.000000
max 755000.000000
Name: SalePrice, dtype: float64

# 柱状图绘制
sns.distplot(df_train['SalePrice']);

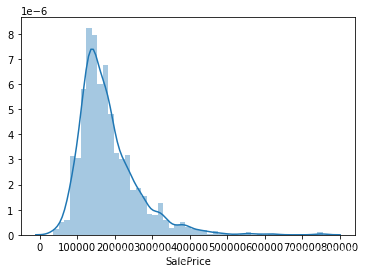
由上图可以看出：SalePrice偏离正态分布，且显示出明显的正偏斜， 且存在峰值。

#输出偏度（偏离正态分布地情况）和峰度（图像顶部尖不尖）
print("Skewness: %f" % df_train['SalePrice'].skew())
print("Kurtosis: %f" % df_train['SalePrice'].kurt())

Skewness: 1.882876
Kurtosis: 6.536282

2.2 分析与相关单变量之间的关系

2.2.1 分析数值型特征

2.2.1.1 探究与GrLivArea之间的关系

var='GrLivArea'
# 左右拼接表
data=pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
# 绘制散点图
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000))

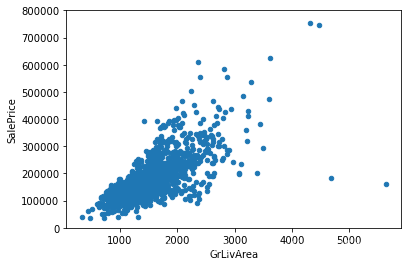
由上图可以看出：两者之间存在一定的线性关系。

2.2.1.2 探究与TotalBsmtSF之间的关系

var='TotalBsmtSF'
# 左右拼接表
data=pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
# 绘制散点图
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000))

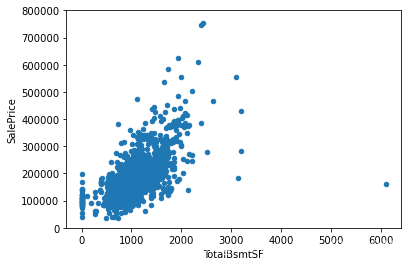
由上图可以看出：两者之间也存在一种强关联关系。

2.2.2 分析类别型数据

2.2.2.1 探究与OverallQual之间的关系

# 类别型数据
var='OverallQual'
# 左右拼接表
data=pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
# 绘制箱式图
f, ax=plt.subplots(figsize=(8, 6))
fig=sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, tmax=800000)

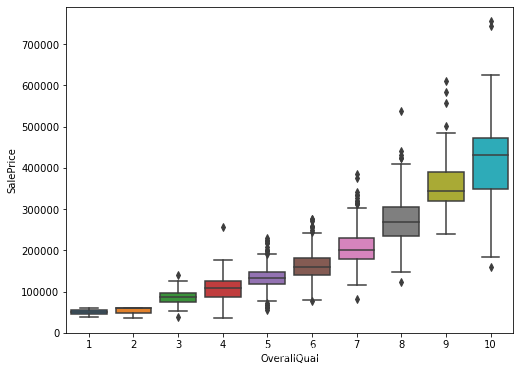
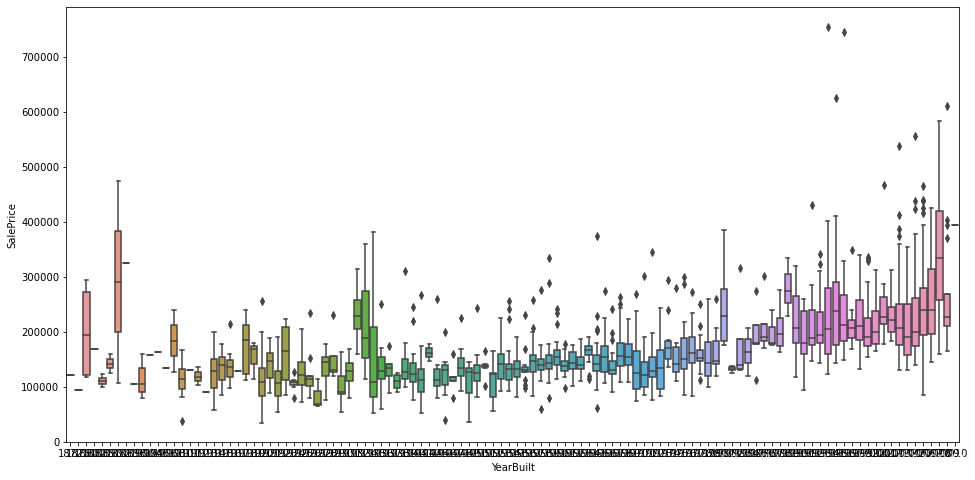
2.2.2.2 探究与YearBuilt之间的关系

# 类别型数据
var='YearBuilt'
# 左右拼接表
data=pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
# 绘制箱式图
f, ax=plt.subplots(figsize=(16, 8))
fig=sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, tmax=800000)

3. 使用热力图客观分析各个变量之间的关系

# 绘制相关性热力图
corrmat=df_train.corr()
f, ax=plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True)

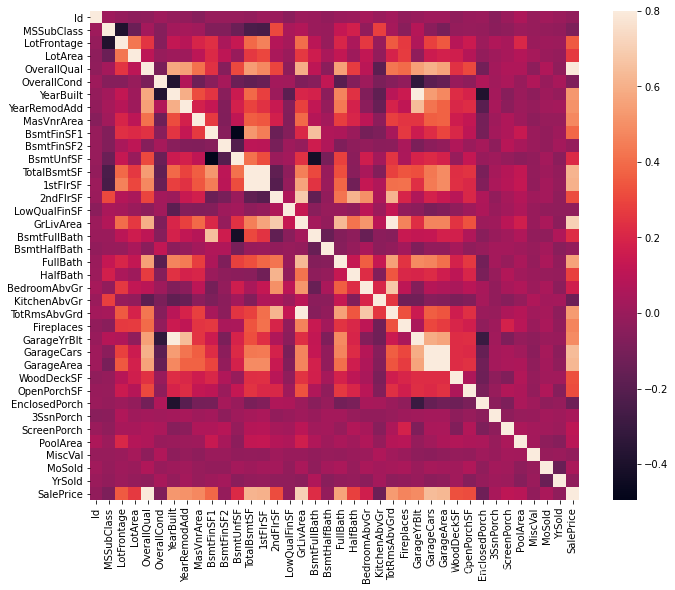
由上图可知：

• TotalBsmtSF和1stFirSF、Garage*的相关性特别强，表明他们之间存在多重共线性的情况；
• 通过看最后一列，可以看到各个变量和SalePrice变量之间的相关性关系；

k=10
# 取相关矩阵中与SalePrice相关性排名前10的特征
cols=corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
# 生成相关矩阵
cm=np.corrcoef(df_train[cols].values.T)
# 调节文字大小
sns.set(font_scale=1.25)
# sns.heatmap参数解释：
# cbar:描述是否绘制颜色条
# annot:如果为True，则在每个热力图单元格中写入数据值。
# annot_kws:当annot为True时，ax.text的关键字参数
# square:如果为True，则将坐标轴方向设置为“equal”，以使每个单元格为方形
# fmt:添加注释时要使用的字符串格式代码
hm=sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f',
              annot_kws={'size':10},yticklabels=cols.values, xticklabels=cols.values)
plt.show()

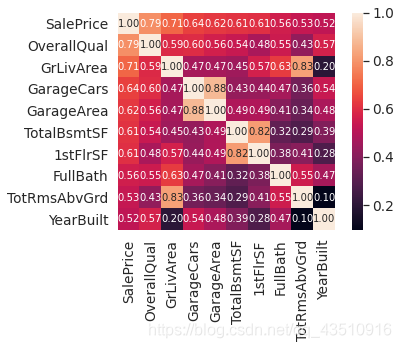
由上图可知：

• GarageCars和GarageArea只需要其中一个变量即可，TotalBsmtSF和1stFlrSF同理。
• TotRmsAbvGrd和GrLivArea之间的相关性也很强。
• YearBuilt和SalePrice之间的相关性也比较强，可能需要一些时间序列处理。

# 去除多重共线性的特征
sns.set()
cols=['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars',
       'TotalBsmtSF', 'FullBath', 'TotRmsAbvGrd', 'YearBuilt']
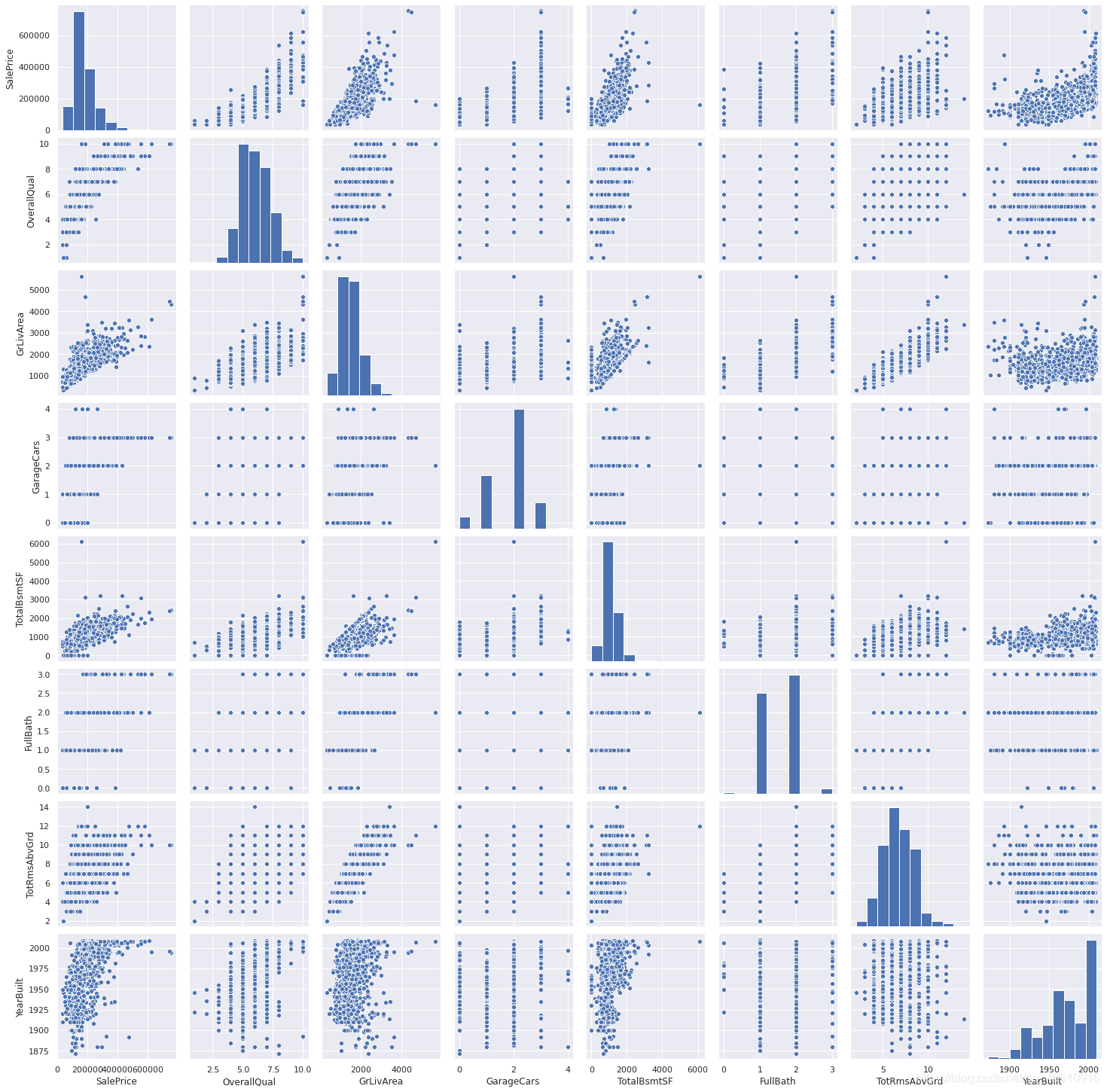
sns.pairplot(df_train[cols], size=2.5)
plt.show()

4. 缺失值处理

思考缺失数据时的重要问题：

• 缺失的数据有多普遍？
• 丢失的数据是随机的还是有规律的？

对这些问题的回答很重要，因为缺少数据可能意味着样本量的减少，这会妨碍我们继续分析。此外，从实质性的角度来看，我们需要确保处理缺失数据的过程不带偏见。

4.1 缺失数据统计

total=df_train.isnull().sum().sort_values(ascending=False)
percent=(df_train.isnull().sum()/df_train.isnull().count()).sort_values(ascending=False)
missing_data=pd.concat([total, percent], axis=1, keys=['Total','Percent'])
missing_data.head(20)

	Total	Percent
PoolQC	1453	0.995205
MiscFeature	1406	0.963014
Alley	1369	0.937671
Fence	1179	0.807534
FireplaceQu	690	0.472603
LotFrontage	259	0.177397
GarageCond	81	0.055479
GarageType	81	0.055479
GarageYrBlt	81	0.055479
GarageFinish	81	0.055479
GarageQual	81	0.055479
BsmtExposure	38	0.026027
BsmtFinType2	38	0.026027
BsmtFinType1	37	0.025342
BsmtCond	37	0.025342
BsmtQual	37	0.025342
MasVnrArea	8	0.005479
MasVnrType	8	0.005479
Electrical	1	0.000685
Utilities	0	0.000000

4.2 缺失数据处理

分析过程：

• 操作：删除PoolQC、MiscFeature、Alley、Fence、FireplaceQu、LotFrontage!
  原因：当超过15%的数据丢失时，我们应该删除相应的变量，并假设它不存在。我们会错过这些数据吗？我不这么认为。这些变量似乎都不是很重要，因为大多数都不是我们买房时考虑的方面（也许这就是数据缺失的原因？）。此外，仔细观察变量，我们可以说’PoolQC’、'miscsfeature’和’FireplaceQu’等变量是异常值的有力候选，因此我们很乐意删除它们。
• 操作：删除GarageCond、GarageType、GarageYrBlt、GarageFinish、GarageQual！
  原因：我们可以看到“GarageX”变量具有相同数量的缺失数据。我认为丢失的数据指的是同一组样本。由于有关车库的最重要信息是用GarageCars表示的，并且考虑到我们只讨论了5%的缺失数据，我将删除提到的“GarageX”变量。同样的逻辑也适用于“BsmtX”变量。
• 操作：删除MasVnrArea、MasVnrType！
  原因：我们可以认为这些变量不是必需的，它们与已经考虑的YearBuilt和OverallQual有很强的相关性。因此，删除也不会丢失信息。
• 操作：删除Electrical中含有缺失值的样本。
  原因：因为它只有一个样本缺失，所以我们将删除此样本并保留变量。

总之，为了处理丢失的数据，我们将删除所有丢失数据的变量，除了变量’Electrical’。在“Electrical”中，我们将删除缺少数据的观测值。

df_train=df_train.drop((missing_data[missing_data['Total']>1]).index, 1)
df_train=df_train.drop(df_train.loc[df_train['Electrical'].isnull()].index)
df_train.isnull().sum().max()

5. 离群值去除

离群值可以显著地影响我们的模型，并且可以成为有价值的信息来源，为我们提供关于特定行为的见解。

5.1 单变量分析

这里主要关注的是建立一个阈值，将观察值定义为异常值。为此，我们将标准化数据。在这种情况下，数据标准化意味着将数据值转换为平均值为0，标准差为1。

# 数据标准化
saleprice_scaled=StandardScaler().fit_transform(df_train['SalePrice'][:,np.newaxis])
low_range=saleprice_scaled[saleprice_scaled[:,0].argsort()][:10]
high_range= saleprice_scaled[saleprice_scaled[:,0].argsort()][-10:]
print('outer range (low) of the distribution:')
print(low_range)
print('\nouter range (high) of the distribution:')
print(high_range)

outer range (low) of the distribution:
[[-1.83820775]
[-1.83303414]
[-1.80044422]
[-1.78282123]
[-1.77400974]
[-1.62295562]
[-1.6166617 ]
[-1.58519209]
[-1.58519209]
[-1.57269236]]
outer range (high) of the distribution:
[[3.82758058]
[4.0395221 ]
[4.49473628]
[4.70872962]
[4.728631 ]
[5.06034585]
[5.42191907]
[5.58987866]
[7.10041987]
[7.22629831]]

由上述数据可以看出：

• 低范围值类似，与0相差不太远。
• 高范围值远远不是0，而7.0的值确实超出范围。
  目前，我们不会将这些值中的任何一个视为异常值，但我们应该小心处理这两个7.0左右的值。

5.2 多变量分析

#bivariate analysis saleprice/grlivarea
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

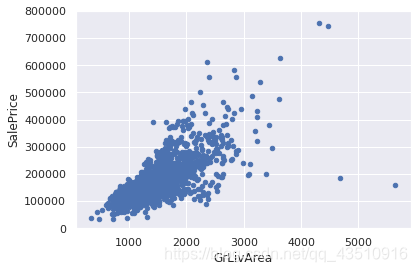
由上图可知：删除“不随大流”的两个离群值。

#deleting points
df_train.sort_values(by = 'GrLivArea', ascending = False)[:2]
df_train = df_train.drop(df_train[df_train['Id'] == 1299].index)
df_train = df_train.drop(df_train[df_train['Id'] == 524].index)

#bivariate analysis saleprice/grlivarea
var = 'TotalBsmtSF'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

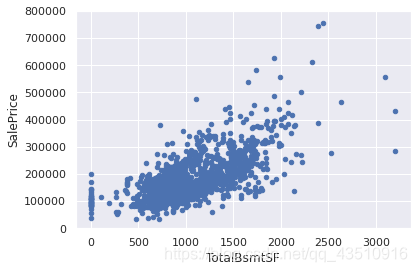
由上图可知：并没有什么需要删除的离群值，大都可以接收就没有必要操作。

6. 检验正态分布

根据Hair等人（2013年）的研究，应检验四个假设：

• 正态性-当我们谈论正态性时，我们的意思是数据应该看起来像正态分布。这一点很重要，因为有几个统计测试依赖于此（例如t-统计）。在本文中，我们将检查“SalePrice”的单变量正态性（这是一种有限的方法）。请记住，单变量正态性不能确保多变量正态性（这是我们想要的），但它有帮助。另一个需要考虑的细节是，在大样本（>200个观测值）中，正态性不是这样一个问题。然而，如果我们解决正态性，我们就避免了很多其他问题（例如异方差），所以这就是我们进行这种分析的主要原因。
• 同方差性-同方差性是指“假设因变量在预测变量范围内表现出相同水平的方差”（Hair等人，2013）。齐次方差是可取的，因为我们希望误差项在自变量的所有值上是相同的。
• 线性-评估线性最常用的方法是检查散点图和搜索线性模式。如果模式不是线性的，那么探索数据转换是值得的。但是，我们将不讨论这个问题，因为我们看到的大多数散点图似乎都具有线性关系。
• 没有关联错误-关联错误，如定义所示，发生在一个错误与另一个错误相关。例如，如果一个正错误系统地产生了一个负错误，这意味着这些变量之间存在着某种关系。这通常发生在时间序列中，其中一些模式与时间相关。我们也不会插手这件事。但是，如果你发现了什么，试着添加一个变量来解释你得到的效果。这是最常见的解决相关错误的方法。

6.1 检验SalePrice的正态性

#直方图-峰度和偏度。
#正态概率图-数据分布应紧跟代表正态分布的对角线。
sns.distplot(df_train['SalePrice'], fit=norm)
fig=plt.figure()
res=stats.probplot(df_train['SalePrice'], plot=plt)

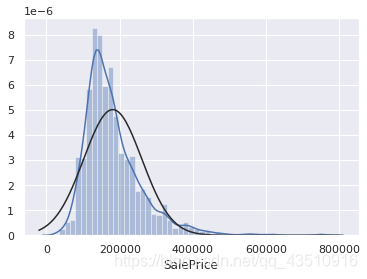
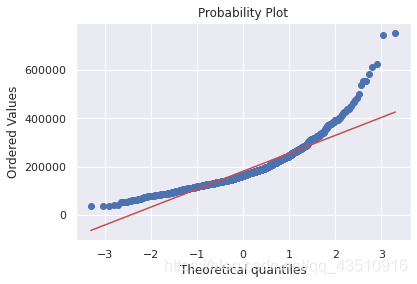
由上图可知：SalePrice不服从正态分布，显示“尖峰”，正偏斜，不遵循对角线。在正偏斜情况下，可以使用对数变换解决这个问题。

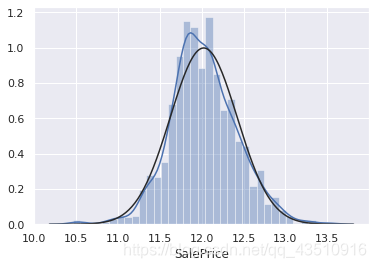
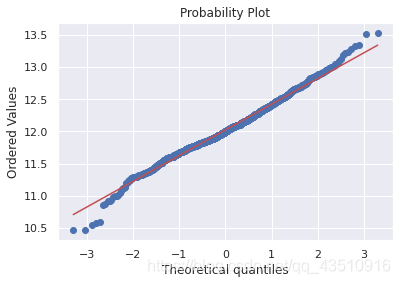
df_train['SalePrice']=np.log(df_train['SalePrice'])

sns.distplot(df_train['SalePrice'], fit=norm)
fig=plt.figure()
res=stats.probplot(df_train['SalePrice'], plot=plt)

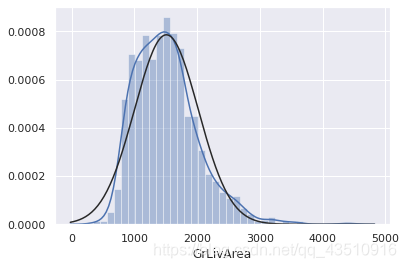
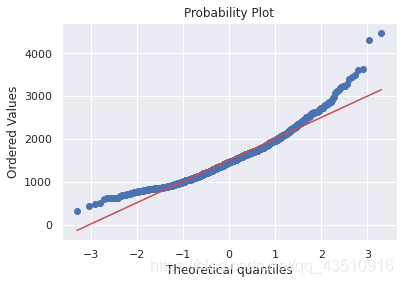
6.2 检验GrLivArea的正态性

sns.distplot(df_train['GrLivArea'], fit=norm)
fig=plt.figure()
res=stats.probplot(df_train['GrLivArea'], plot=plt)

df_train['GrLivArea']=np.log(df_train['GrLivArea'])
sns.distplot(df_train['GrLivArea'], fit=norm)
fig=plt.figure()
res=stats.probplot(df_train['GrLivArea'], plot=plt)

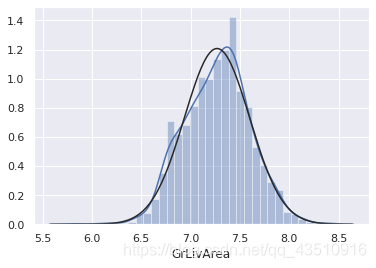
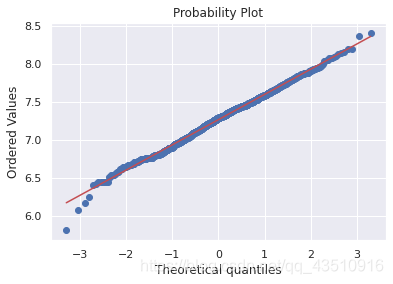
6.3 检验TotalBsmtSF的正态性

#histogram and normal probability plot
sns.distplot(df_train['TotalBsmtSF'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['TotalBsmtSF'], plot=plt)

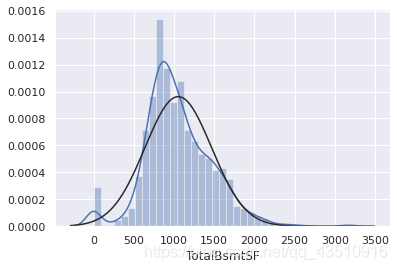
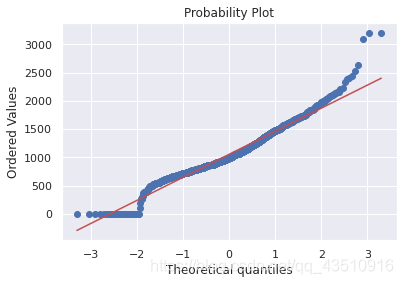
由上图可知：总的来说，呈现正偏斜的情况且大量的观测值为零（没有地下室的房子），但是值0不允许我们进行日志转换。
要在这里应用log转换，我们将创建一个变量，该变量可以获得有或没有地下室（二进制变量）的效果。然后，我们将对所有非零观测值进行对数变换，忽略那些值为零的观测值。这样我们就可以转换数据，而不会失去有无地下室的效果。

df_train['HasBsmt']=pd.Series(len(df_train['TotalBsmtSF']), index=df_train.index)
df_train['HasBsmt']=0
df_train.loc[df_train['TotalBsmtSF']>0,'HasBsmt']=1

df_train.loc[df_train['HasBsmt']==1, 'TotalBsmtSF']=np.log(df_train['TotalBsmtSF'])

#histogram and normal probability plot
sns.distplot(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], plot=plt)

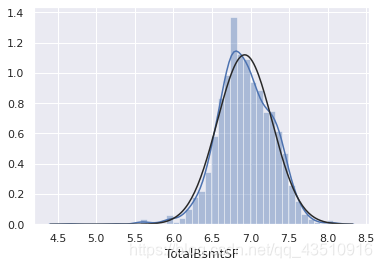
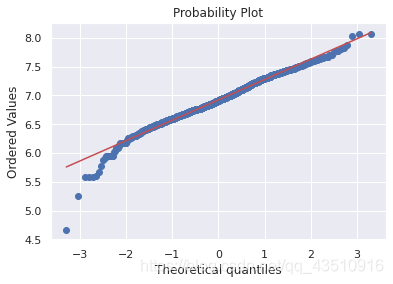
7. 检验同方差性

检验两个变量同方差性的最佳方法是图解法。偏离等离散度的形状如圆锥体（图形一侧的小离散度，另一侧的大离散度）或菱形（分布中心的大量点）。

7.1 检验SalePrice和GrLivArea的同方差性

#scatter plot
plt.scatter(df_train['GrLivArea'], df_train['SalePrice']);

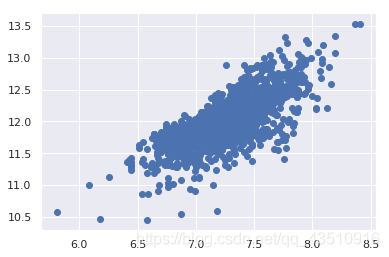
对数变换之前的图像（旧版本）：

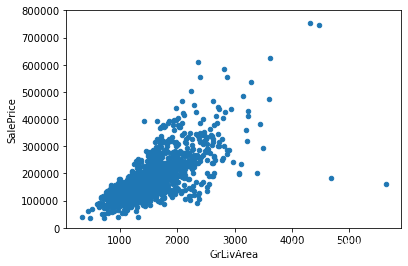
由上述两图对比可知：这个旧版本的散点图（在对数变换之前）有一个圆锥形状。如您所见，当前散点图不再是圆锥形状。这就是正态化的力量！通过保证某些变量的正态性，我们就解决了同方差问题。

7.2 检验SalePrice和TotalBsmtSF的同方差性

#scatter plot
plt.scatter(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], df_train[df_train['TotalBsmtSF']>0]['SalePrice']);

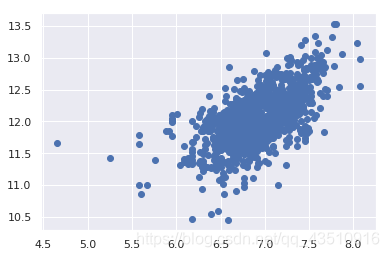
我们可以说，一般来说，“销售价格”在“TotalBsmtSF”范围内表现出相同水平的方差。

8. 特征提取

df_train=pd.get_dummies(df_train)

完结撒花~以上就是数据分析的全部内容，但是任务还没有结束，接下来使用的预测模型，我将在下一篇博客中继续解析Top大佬们的Gold方案！

下集预告：Stacked Regressions : Top 4% on LeaderBoard by Serigne

创作不易，点个赞再走吧Ծ‸Ծ