【动手学深度学习】卷积神经网络_LeNet

卷积神经网络（LeNet）

本文为李沐老师《动手学深度学习》一书的学习笔记，原书地址为：Dive into Deep Learning。

1. 网络结构

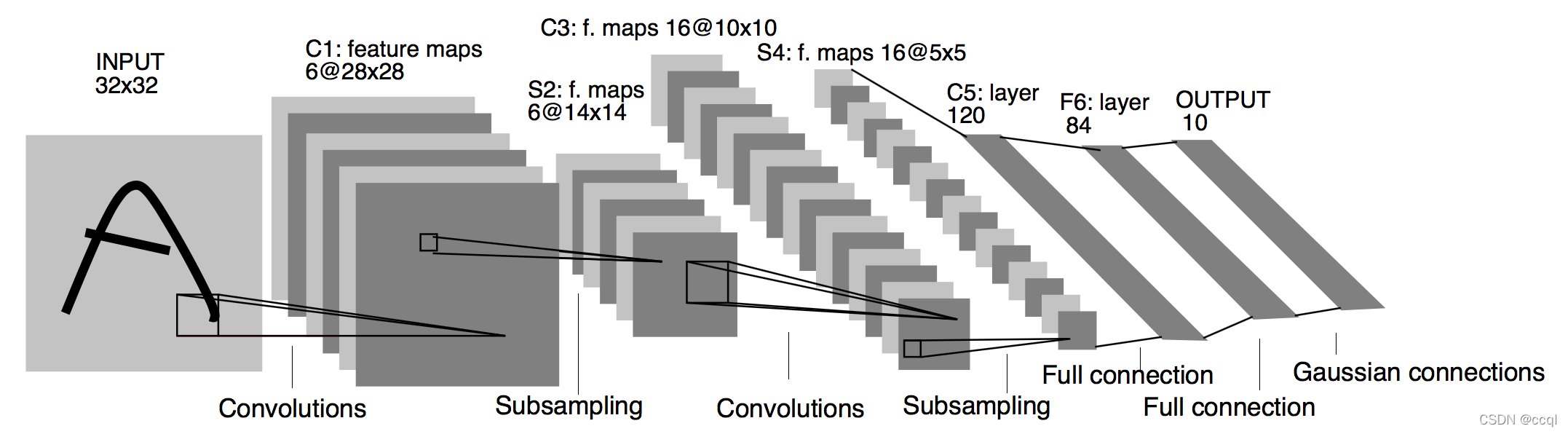
网络结构计算过程：

假设输入形状是$n_h\times n_w$，卷积核窗口形状是$k_h\times h_w$，在高的两侧一共填充$p_h$行，在宽的两侧一共填充$p_w$列，高上步幅为$s_h$，宽上步幅为$s_w$，则卷积输出形状计算公式：$\lfloor (n_h-k_h+p_h+s_h)/s_h\rfloor \times \lfloor (n_w-k_w+p_w+s_w)/s_w\rfloor$

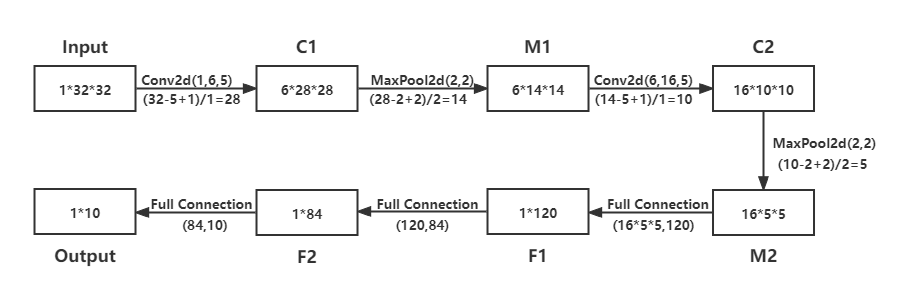
2. 网络结构说明

LeNet分为卷积层块和全连接层块两个部分。

卷积层块里的基本单位是卷积层后接最大池化层：卷积层用来识别图像里的空间模式，如线条和物体局部，之后的最大池化层则用来降低卷积层对位置的敏感性。卷积层块由两个这样的基本单位重复堆叠构成。在卷积层块中，每个卷积层都使用$5\times 5$的窗口，并在输出上使用sigmoid激活函数。第一个卷积层输出通道数为6，第二个卷积层输出通道数则增加到16。这是因为第二个卷积层比第一个卷积层的输入的高和宽要小，所以增加输出通道使两个卷积层的参数尺寸类似。卷积层块的两个最大池化层的窗口形状均为$2\times 2$，且步幅为2。由于池化窗口与步幅形状相同，池化窗口在输入上每次滑动所覆盖的区域互不重叠。

3. 代码实现

import time
import torch
import torchvision
import torchvision.transforms as transforms
from torch import nn, optim

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2), # kernel_size, stride
            nn.Conv2d(6, 16, 5),
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2)
        )
        self.fc = nn.Sequential(
            nn.Linear(16*4*4, 120),
            nn.Sigmoid(),
            nn.Linear(120, 84),
            nn.Sigmoid(),
            nn.Linear(84, 10)
        )

    def forward(self, img):
        feature = self.conv(img)
        output = self.fc(feature.view(img.shape[0], -1))# 先数据扁平化，再输入全连接层
        return output
net = LeNet()
print(net)

4. 问题发现及解决

Q：lenet模型传播函数的output = self.fc(feature.view(img.shape[0], -1))这句代码的理解？

A：卷积层计块算出来后将数据扁平化再输入全连接层块进行运算，img的形状为[256, 1, 28, 28]，feature的尺寸为[256, 1, 16, 4, 4]，经过这句代码运算后feature.view(img.shape[0], -1)张量的尺寸为[256, 256]。也就是说，全连接层的输入形状将变成二维，其中第一维是小批量中的样本，第二维是每个样本变平后的向量表示，且向量长度为通道、高和宽的乘积。