多输入通道和多输出通道的卷积计算

1. 输入通道数为$n$，输出通道数为$1$

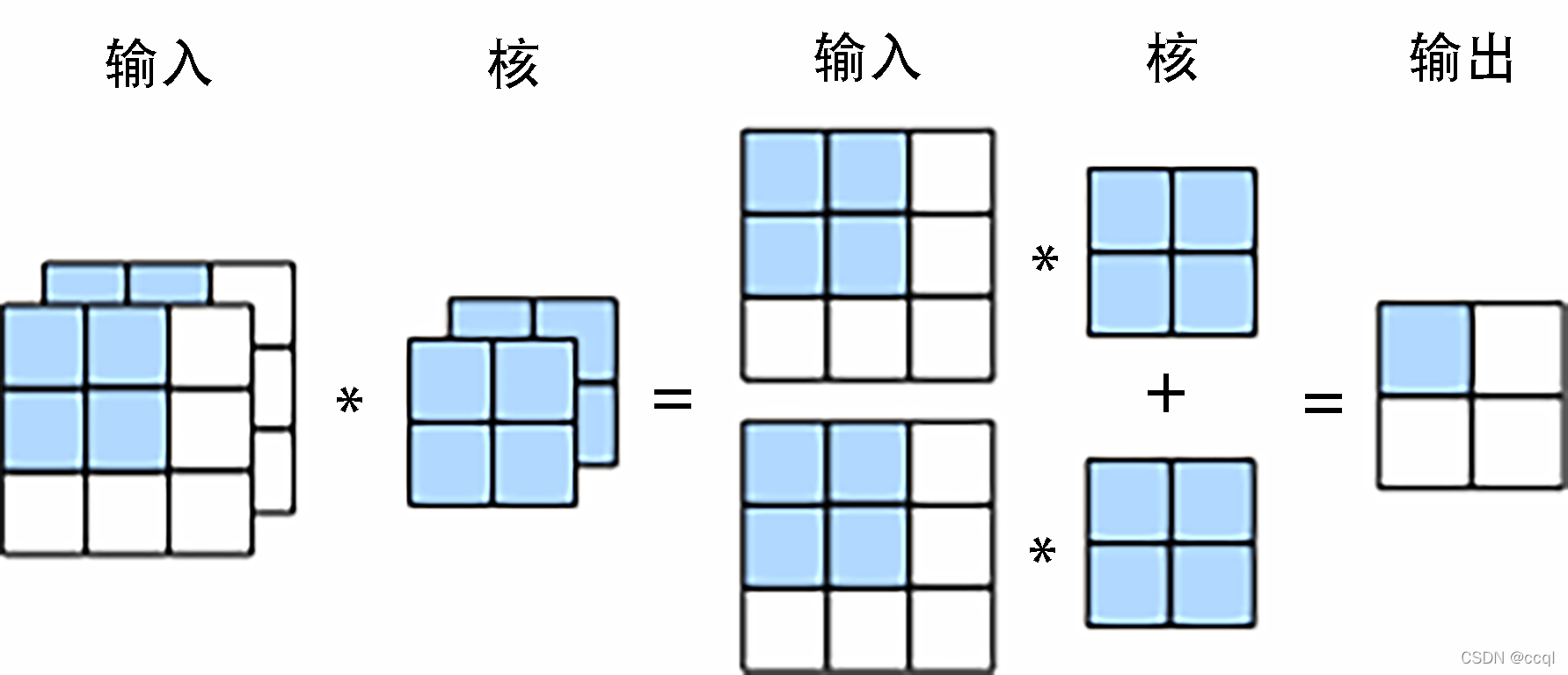
当输入数据含多个通道时，我们需要构造一个输入通道数与输入数据的通道数相同的卷积核，从而能够与含多通道的输入数据做互相关运算。
例如：含$2$个输入通道的二维互相关计算的例子。在每个通道上，二维输入数组与二维核数组做互相关运算，再按通道相加即得到输出。图中阴影部分为第一个输出元素及其计算所使用的输入和核数组元素：$(1\times 1+2\times 2+4\times 3+5\times 4)+(0\times 0+1\times 1+3\times 2+4\times 3)=56$。

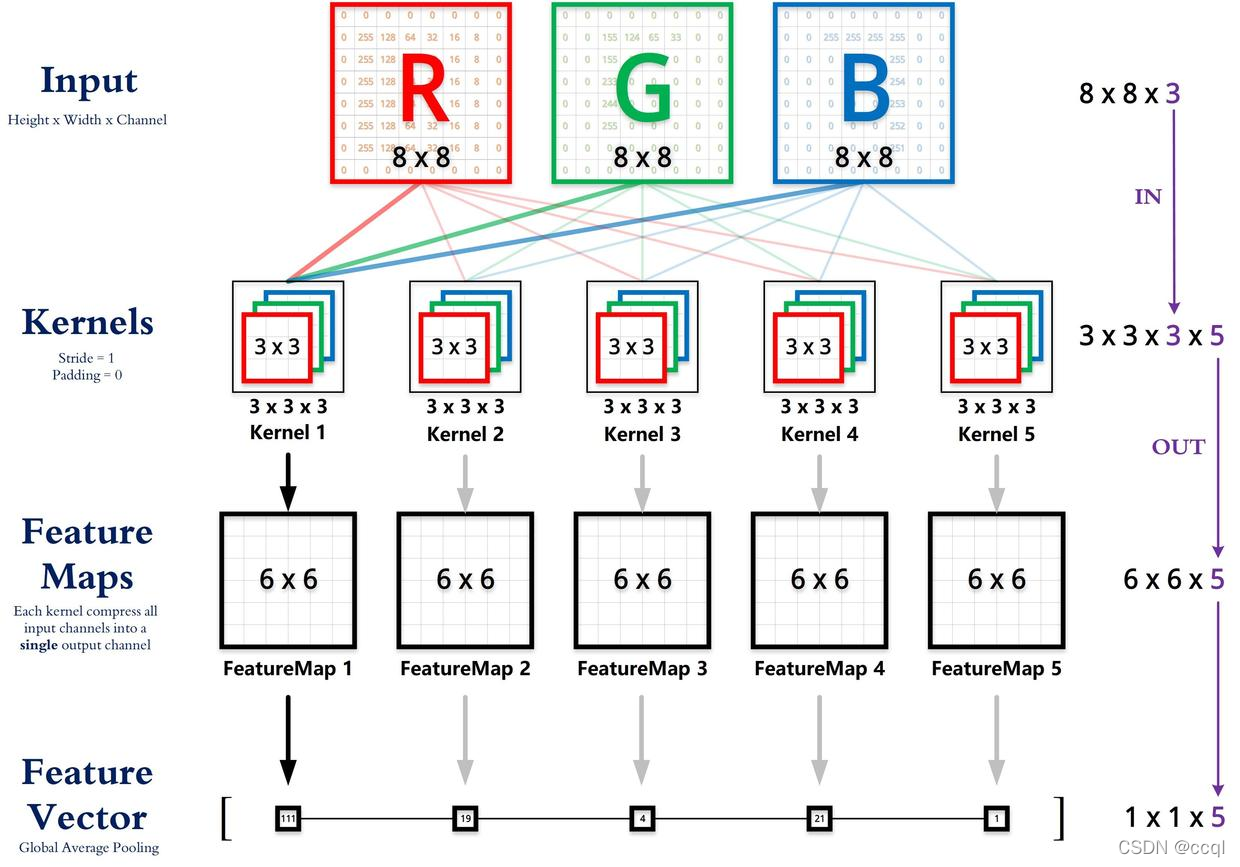
2. 输入通道数为$n_i$，输出通道数为$n_j$

其实与上一个情况很相似，因为我们希望得到含多个通道的输出，所以可以为每个输出通道分别创建形状为$n_i\times k_h\times k_w$的核数组。将它们在输出通道维上连结，卷积核的形状即$n_i\times n_j\times k_h\times k_w$。在做互相关运算时，每个输出通道上的结果由卷积核在该输出通道上的核数组与整个输入数组计算而来。这段话说得比较晦涩，不如下图更形象些。

3. $1\times 1$卷积层

1×1卷积失去了卷积层可以识别高和宽维度上相邻元素构成的模式的功能。实际上，1×1卷积的主要计算发生在通道维上。假设我们将通道维当作特征维，将高和宽维度上的元素当成数据样本，那么1×1卷积层的作用与全连接层等价，所以1×1卷积层被当作保持高和宽维度形状不变的全连接层使用。于是，我们可以通过调整网络层之间的通道数来控制模型复杂度。