Calatan Number
calatan数的定义
卡特兰数的定义为：
由n个"+1"和n个"-1"构成的2n项：\(a_{1}、a_{2}、a_{3}、...、a_{2n}\)其部分和满足：\(a_{1}+a_{2} + a_{3}+...+a_{k}\geqslant0 \qquad k = 1,2,...,2n\)的数列为第n个卡特兰数。
Calatan数的公式
卡特兰数的递推公式：[1]
令$ h(0) = 1,h(1) = 1 \(则calatan数满足递归式：</br>
     \) h(n) = h(0)h(n-1) + h(1)h(n-2) + ...+ h(n-1)h(0) ;n >= 2$
另类递推公式：
$h(n) = h(n-1)(4n-2)/(n+1) $
该递推关系的解为：
\(C_n = {1 \above{1pt} n+1}\dbinom{2n}{n}\)
卡特兰数：
$C_0 = 1 $
$C_1 = 1 $
$C_2 = 2 $
$C_3 = 5 $
$C_4 = 14 $
$C_5 = 42 $
calatan的应用
1.括号匹配问题
由n个左括号和n个右括号组成的有效表达式的个数，是第n个卡特兰数。
正如 \(C_3 = 5\),即如下所示：
2. 进出栈问题
一个足够大的栈的进栈序列为 $ 1,2,3,...n $ ,则其有多少个不同的出栈顺序？
我们可以这样想，假设k是最后一个出栈的数，比k早进栈且早出栈的数有k-1个，一共有h(k-1)种方案；比k玩进栈且早出栈的数有n-k个，一共有h(n-k)种方案。所以一共的出栈方案有$ h(k-1)*h(n-k) $种方案。显而易见，k取不同值时，产生的出栈序列是相互独立的，因为k的值为从1到n，所以出栈方案为：
$ h(n) = h(0)*h(n-1) + h(1)*h(n-2) + ...+ h(n-1)h(0) $
2. 电影购票问题
电影票每张50元，如果有m+n个人排队买票，其中m个人各持有50元面值的钞票张，另外n个人各持有100元面值的钞票张，而票房没有预备找零．有多少种方法可以将这个人排成一列，顺序购票，使得无需因为等待找零而耽误时间.
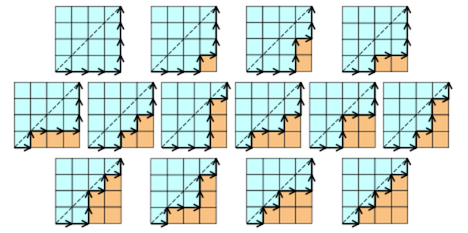
如上图所示，在nxn的方格中，从一个角到另一个角（成对角线），不能跨越对角线的路径数。
只要将向右记为+1，向上记为-1,问题就转化为了进出栈问题。
具体参考文献 [2]
代码实现
#include <iostream>
using namespace std;
// A recursive function to find nth catalan number
unsigned long int catalan(unsigned int n)
{
// Base case
if (n <= 1)
return 1;
// catalan(n) is sum of catalan(i)*catalan(n-i-1)
unsigned long int res = 0;
for (int i = 0; i < n; i++)
res += catalan(i) * catalan(n - i - 1); //h(n) = h(0)*h(n-1) + h(1)*h(n-2)+h(2)*h(n-3)+...+h(n)
return res;
}
// Driver program to test above function
int main()
{
for (int i = 0; i < 10; i++)
cout << catalan(i) << " ";
return 0;
}
