快速排序

bubblesort

insrtionsort

selectionsort

mergesort

bucketsort

countingsort

radixsort

heapsort

tournametsort

 

---

 

A 快速排序：

　　mergesort的计算量和难点在于合，而quicksort在于分

 B轴点：

　　轴点左侧的元素都比它小，右侧的元素都比它大。 所以一旦当我们确定待排序列的轴点，快速排序的核心就是确定序列的轴点。

 　　 坏消息：在原始序列中，轴点未必存在。

　　必要条件：轴点必然已经就位。即它在当前序列中所对应的秩，必然等于它在有序序列中所对应的秩。

　　任何元素都非就位的序列必然存在，即乱排序序列（derangement）

　　在有序序列中，所有元素皆为轴点，反之亦然。

　　所谓的快速排序，就是将所有元素转换为轴点的过程。

　　好消息：适当交换元素的位置，可使任一元素抓换为轴点。

 　　

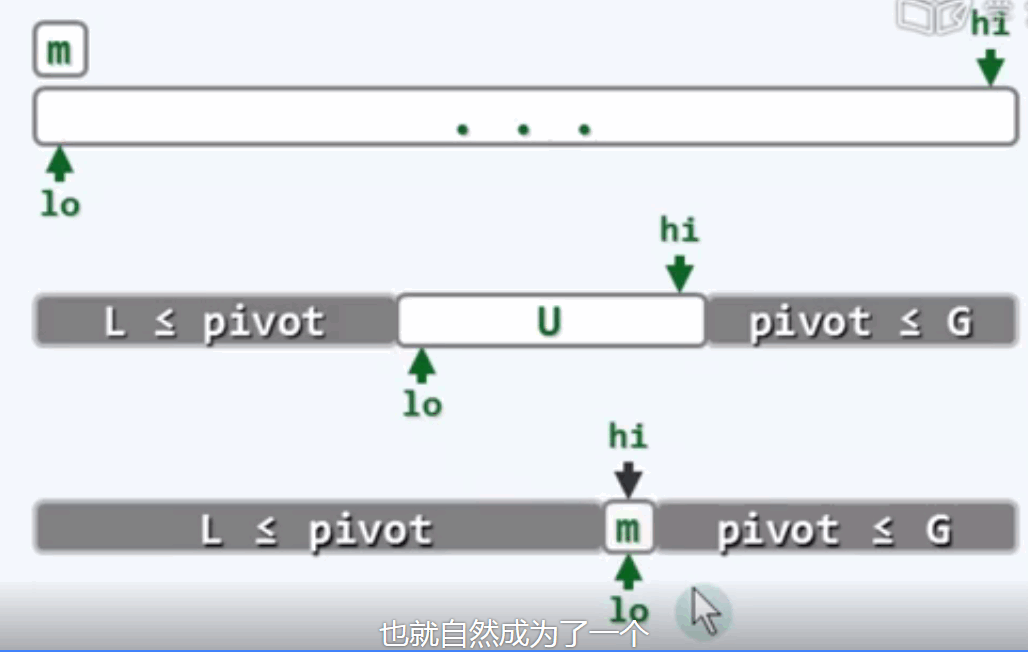
　　利用lo和hi将序列分为三部分，尝试将lo与hi向内侧移动，从而将它们彼此靠近。

　　lo每向后移动一步，L向后拓展一个单位。hi每向前移动一步，G向前移动一步。我们将U中的每个元素加入到L或者G中。

　　最终lo与hi同时指向同一个位置时，那么这个候选者自然成为了一个名副其实的轴点。

 

 

从数值上看，

 

　　先选择末元素作为候选轴点hi,然后不断比较U中的值与候选轴点的大小，如果候选轴点的值是小于序列U中的值的，那么不断的将U中的值移入G。此时G会不断吞噬U区间。

　　直到序列中的值不再小于候选轴点的值，此时交换hi与lo的位置，继续判断序列U与候选轴点lo的大小，如果U中的值是小于lo处的值的，那么将lo不断右移，此时L会不断吞噬U区间。

　　当最终子序列U只有一个单元时，此时将候选轴点植入为1的这个单元，此时完成了一个对原序列的一个快速划分。

C实例：

D性能分析：

　　在经过划分之后，不能保证稳定性。 lo/hi的移动方向相反，左/右侧的大/小重复元素可能前/后颠倒。

　　空间复杂度为O（1），

　　时间复杂度： 2 * T(n/2) + O(n) = T(n) = O（nlogn），但是划分的均衡性完全取决于初始候选轴点的秩，

　　最好情况： 每次划分都接近于平均，轴点总是接近中央。

　　　　　　T（n） = 2 x T((n-1)/2) + O(n) = O(nlogn)

　　最坏情况： 

　　　　　　T（n） = T(n-1) + T(0) + o（n） = O(n2)  //与起泡排序相当。

　　平均性能： 

　　　　O(nlogn)

　　假设所有元素都是均匀分布：

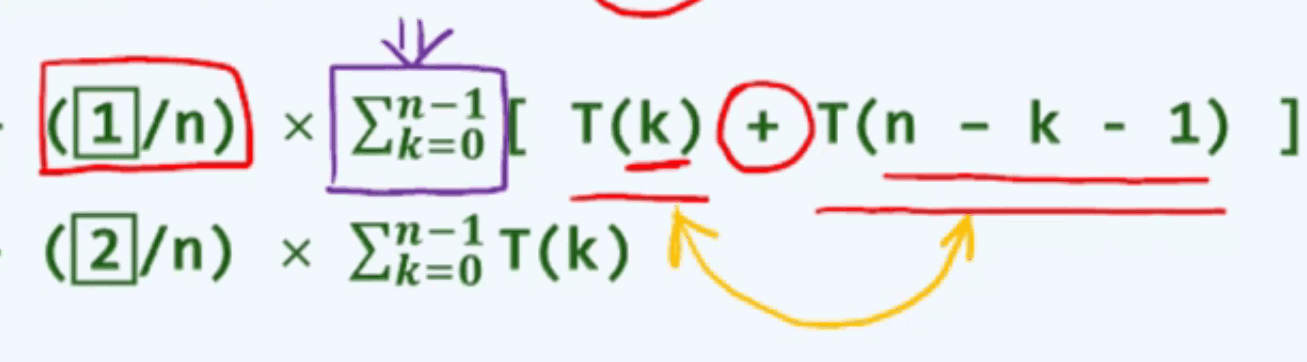
　　　　假设初始轴点在序列U中的秩为k,那么经过partition后，输出的子序列L的平均运行时间为T(k),那么子序列G的平均运行时间为T（n-k-1）

　　

 

 

 

　E变种：

 每一次迭代我们考察的都是当前序列U的首元素，也就是由K指定的那个元素。我们将根据x的数值大小，将它归入L或G，如果候选轴点小于当前元素S[k]，那么将k后移一个单位。如果此时x小于候选轴点，那么应该将x归入L中，我们选择一种变通的方法将x加入L中，即滚动移动，将G的首元素挪动至第一个位置，swap(S[++mi],S[k++])

 　　F：实现