红黑树

 

 

 

 

 

 

 

 

 

 

 

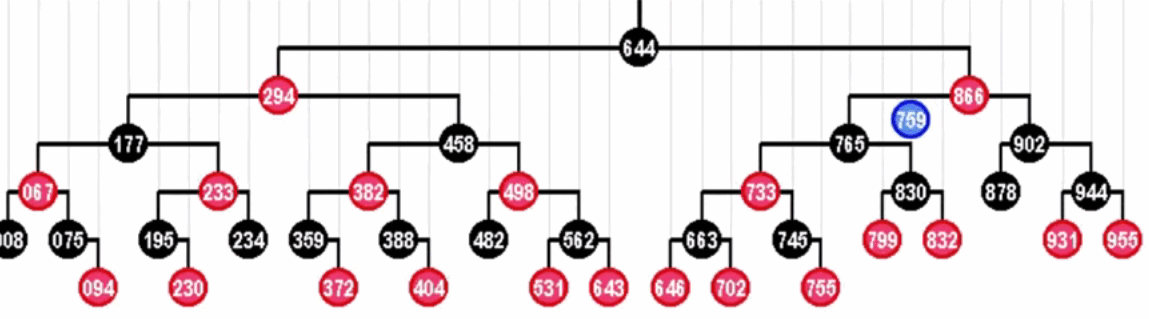
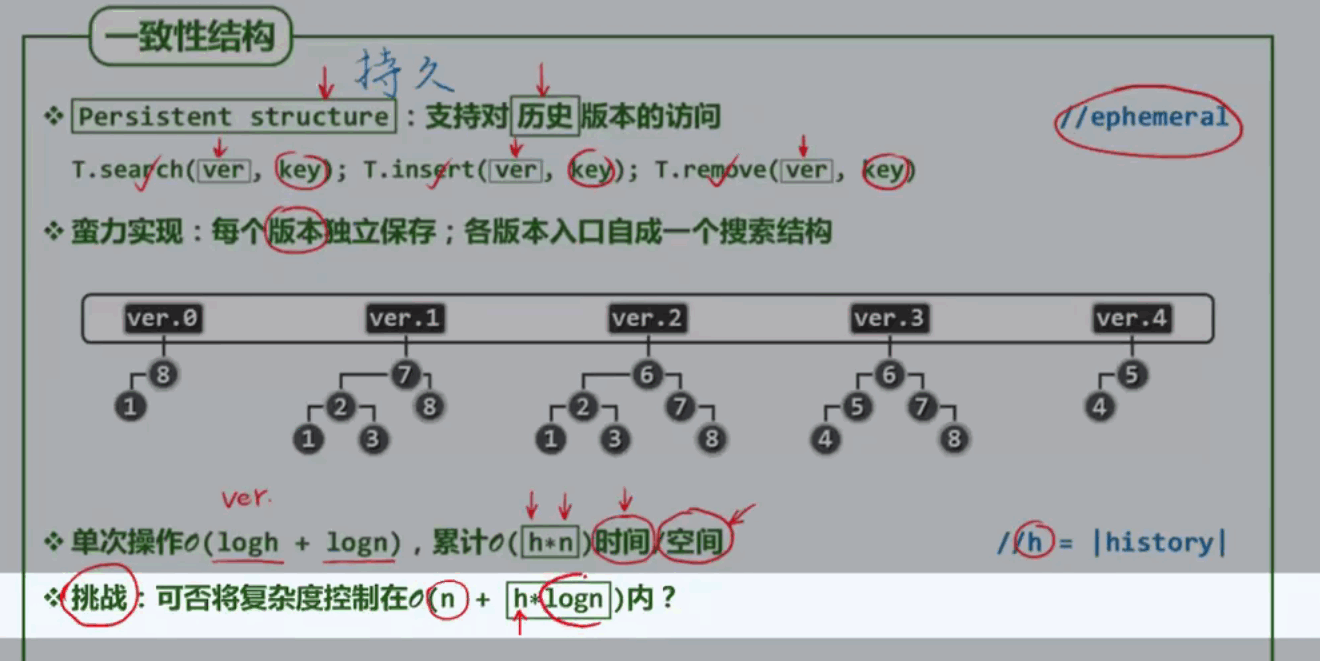
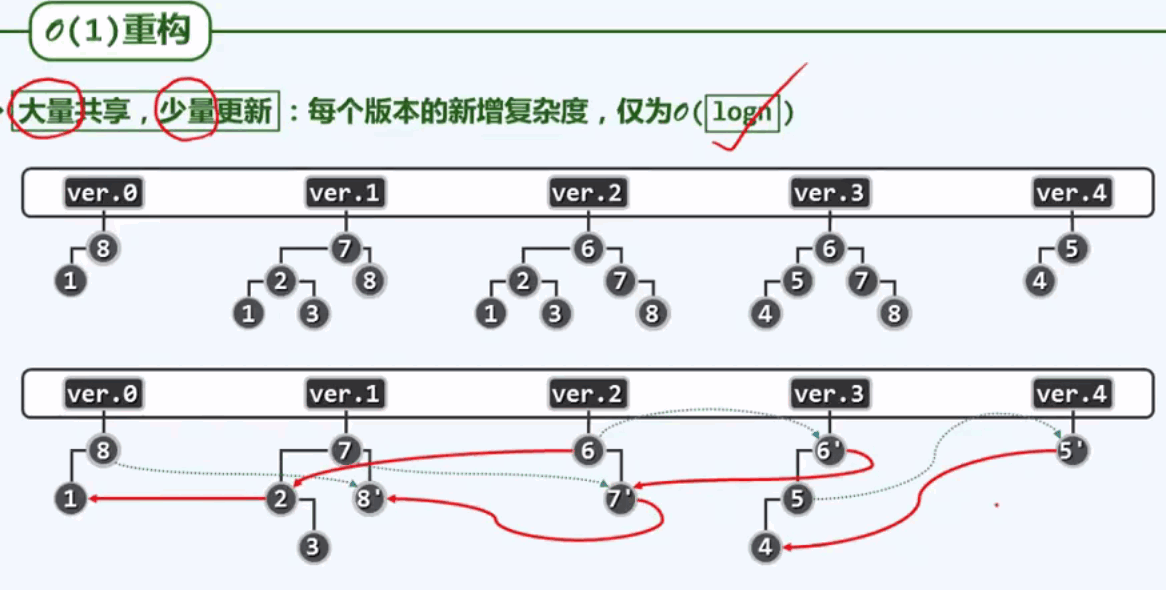
 问题：

　　能否进一步提高，比如总体O（n+h）、单版本O(1)？ 答案是可以！！

---

 

相邻的版本之间的差异不能超过O（1）,显然AVL树的删除操作不能满足这一点，因为当每次删除一个节点后，有可能自底而上，逐层引发多大logN次的旋转。

 

 

 

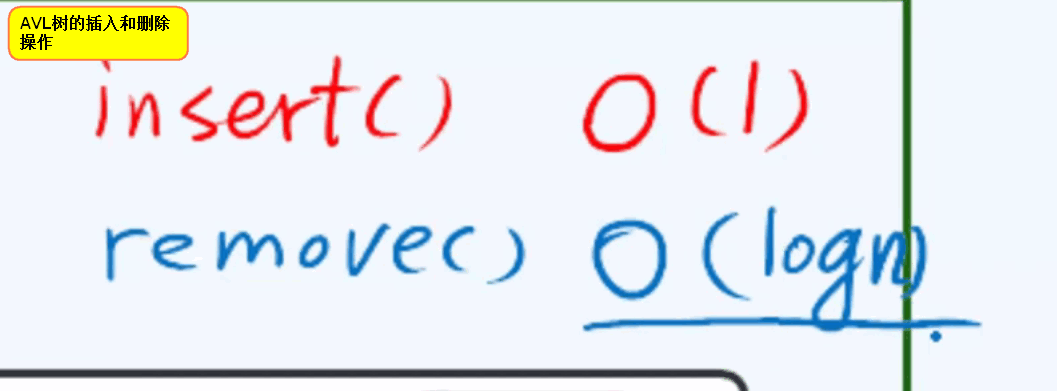
所以要用到红黑树：

　

---

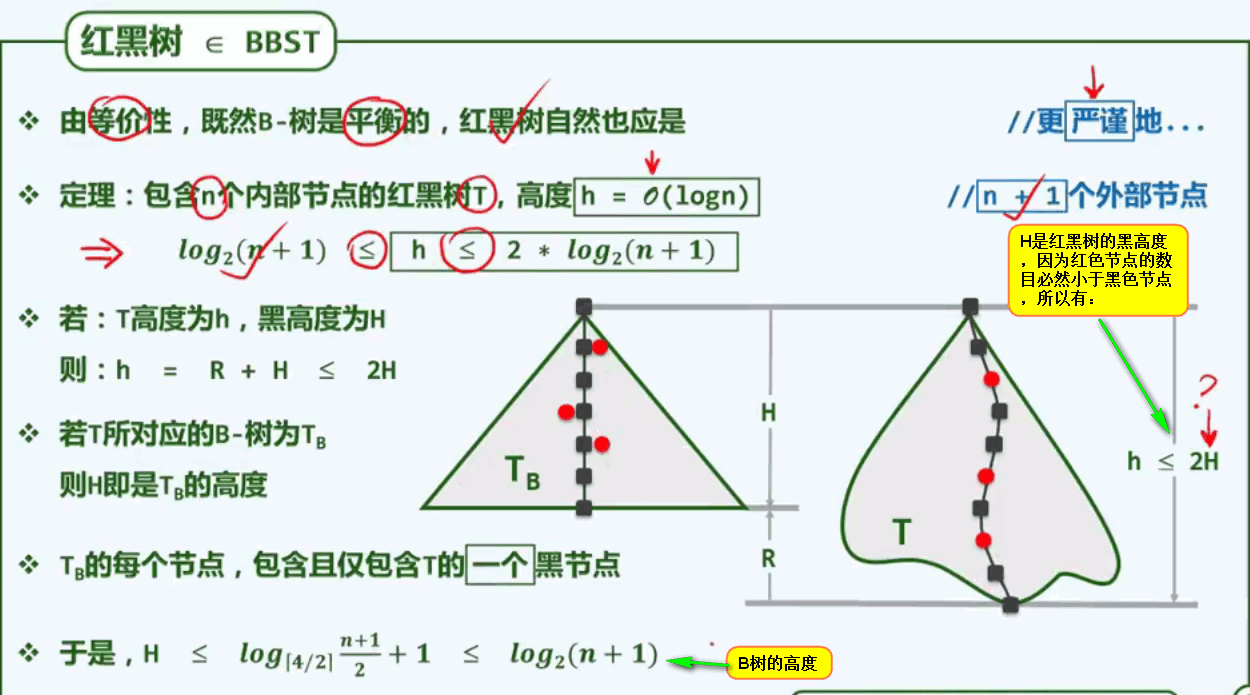
　红黑树所具有的规则：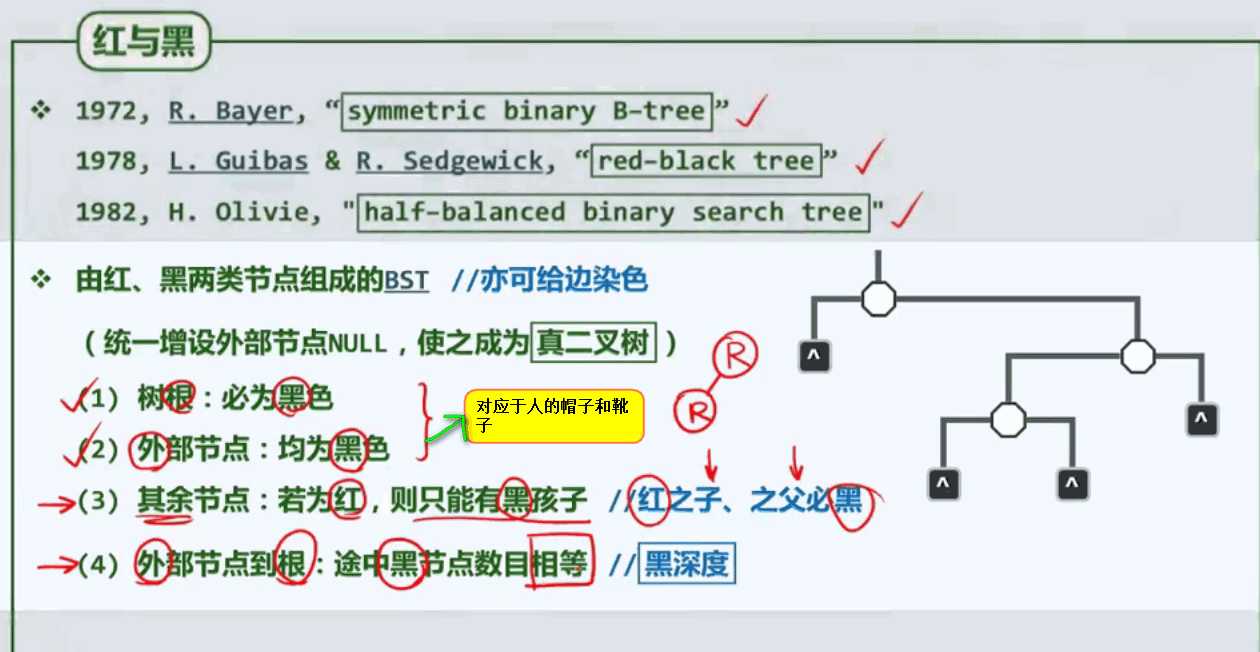

 

 

 

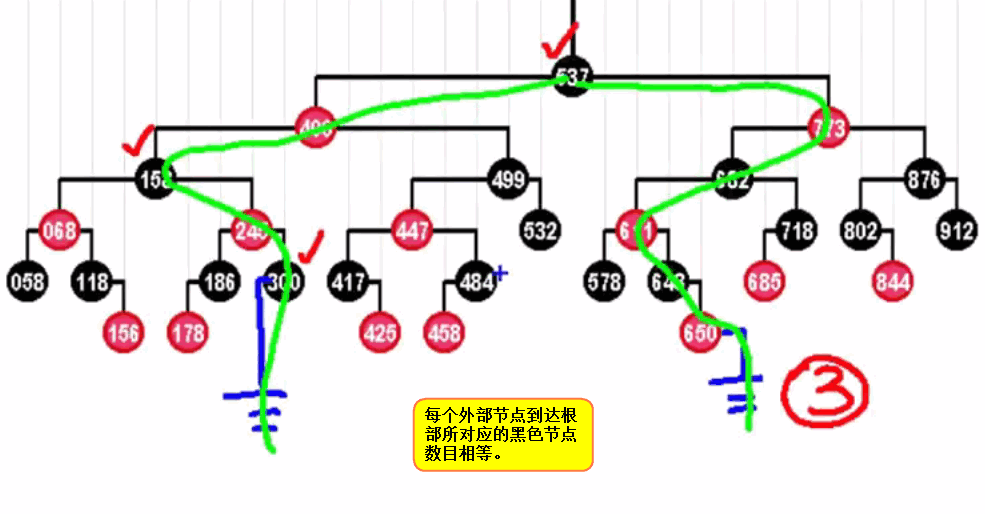
 对红色节点做一次提升变换：

 

 

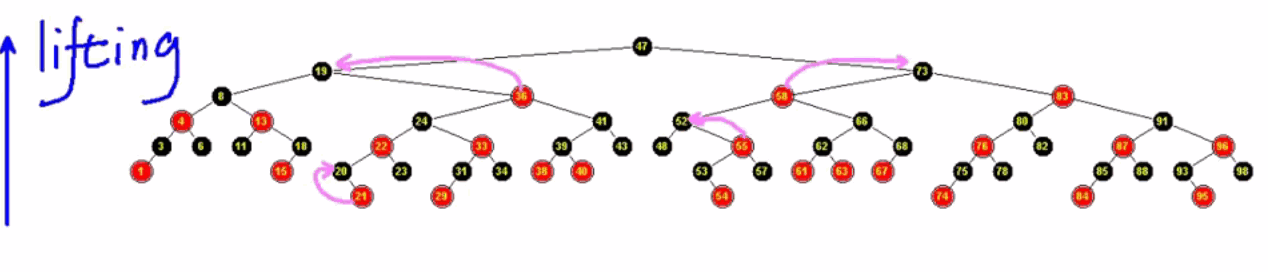
　　底层节点：

 

 

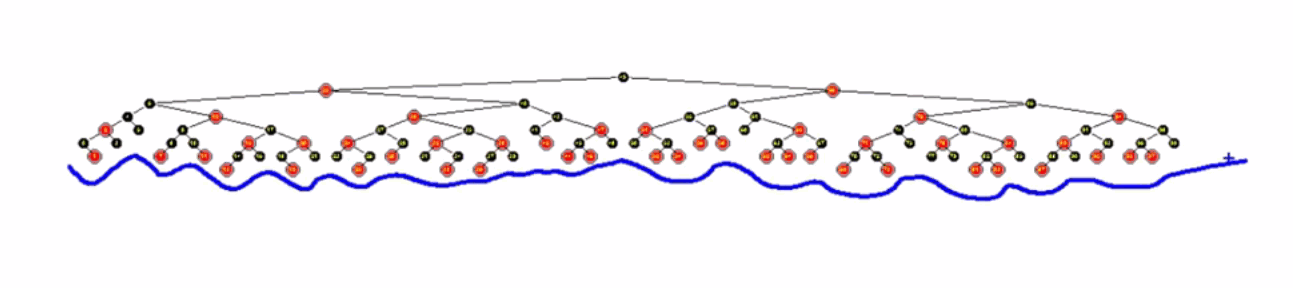在经过提升之后：

 

　　

 

 原来提升之后的红黑树就是4阶B树啊！！！

 

 

 

 

---

 

 红黑树接口定义：　　

　　

 

 

---

 

红黑树的动态调整算法：

　　插入：

 

 

 

 

 

 

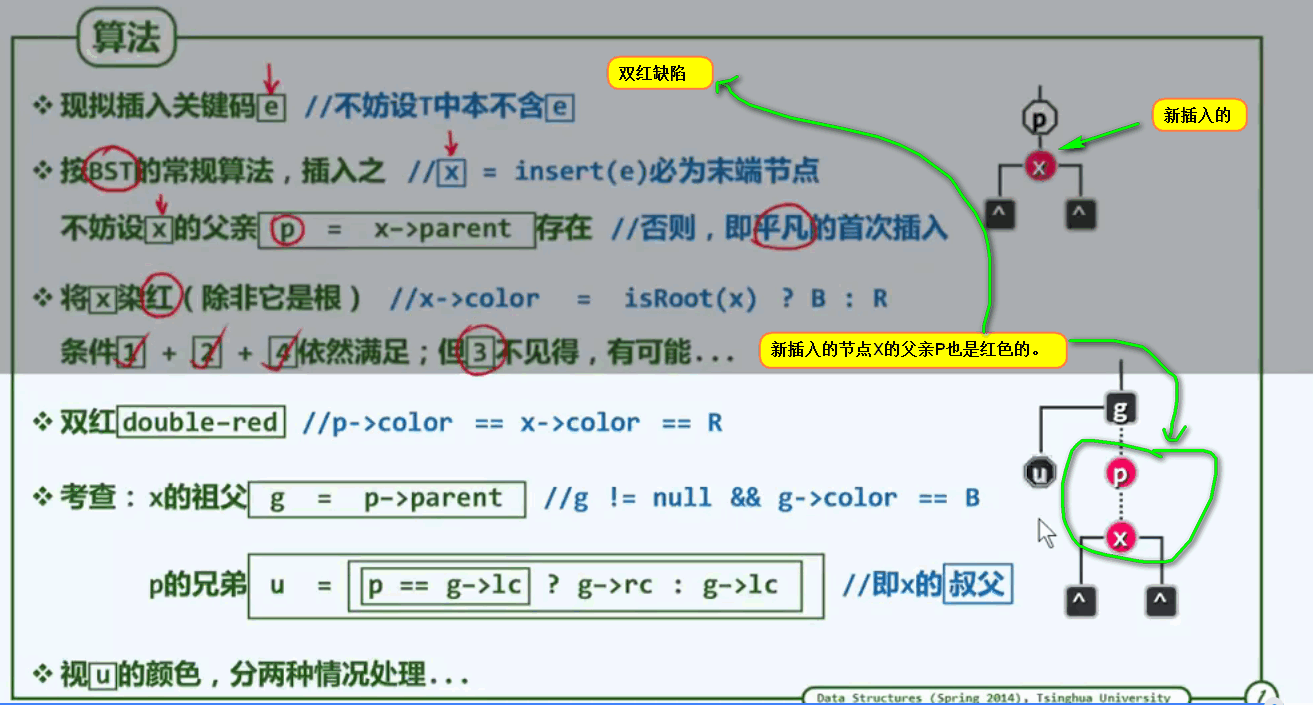
双红修正算法：

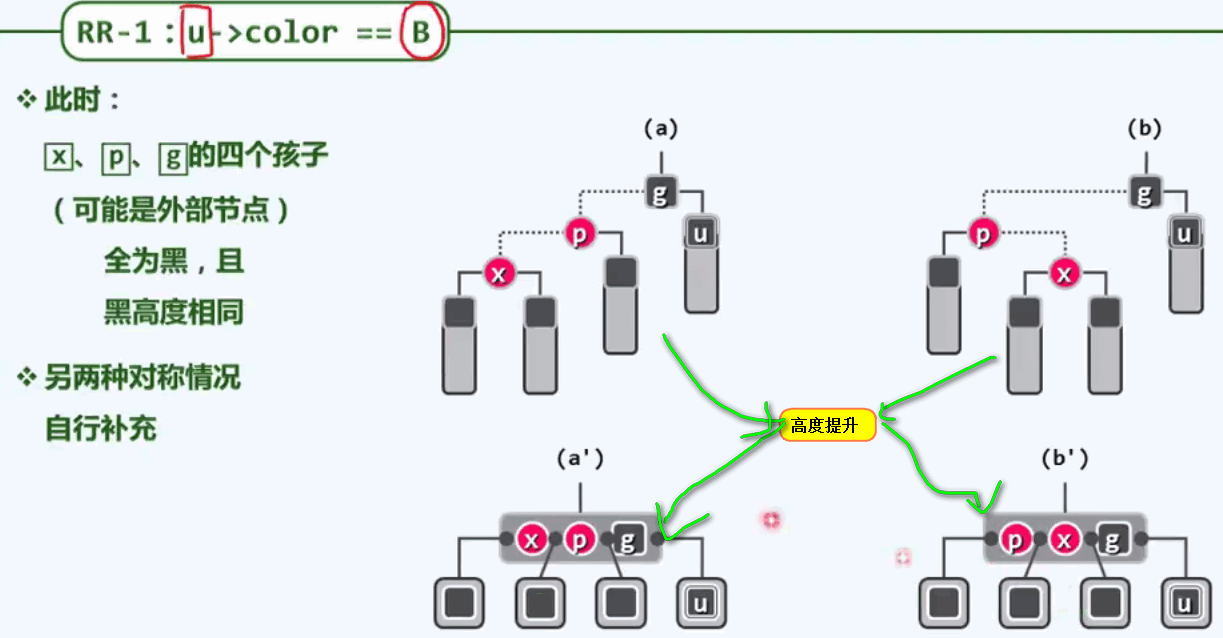
　　第一种情况：叔父节点u是黑色的

　　

 

 

 

 

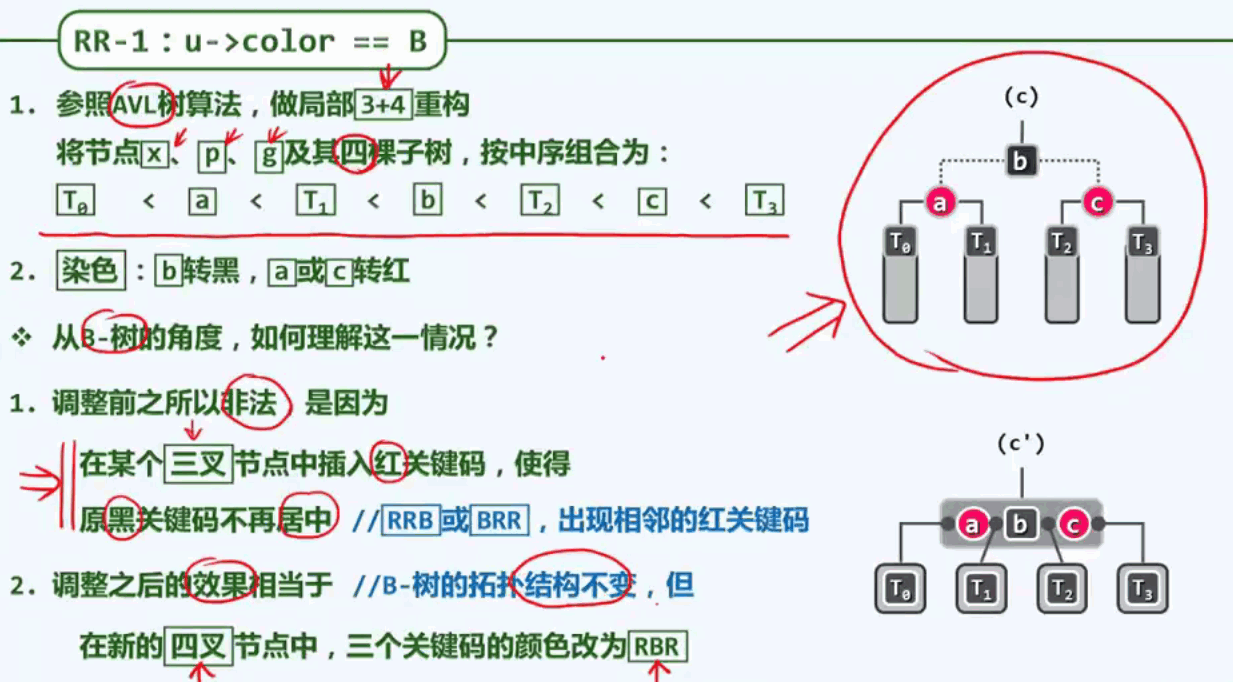
　第二种情况：叔父节点u是红色的

　　

 

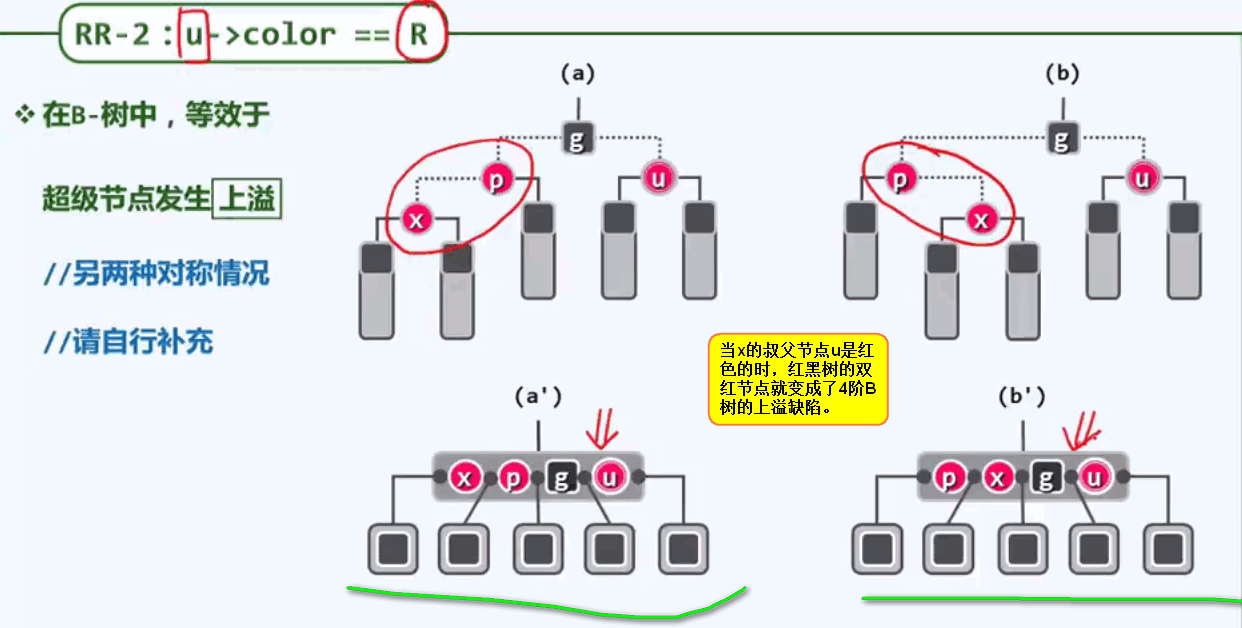
 需要在出现问题的节点中，找到居中的那个关键码，并且以他为界，将原先的大节点分为左右两个新的节点。居中分界的关键码，将被取出上移插入父节点的位置中。

　　

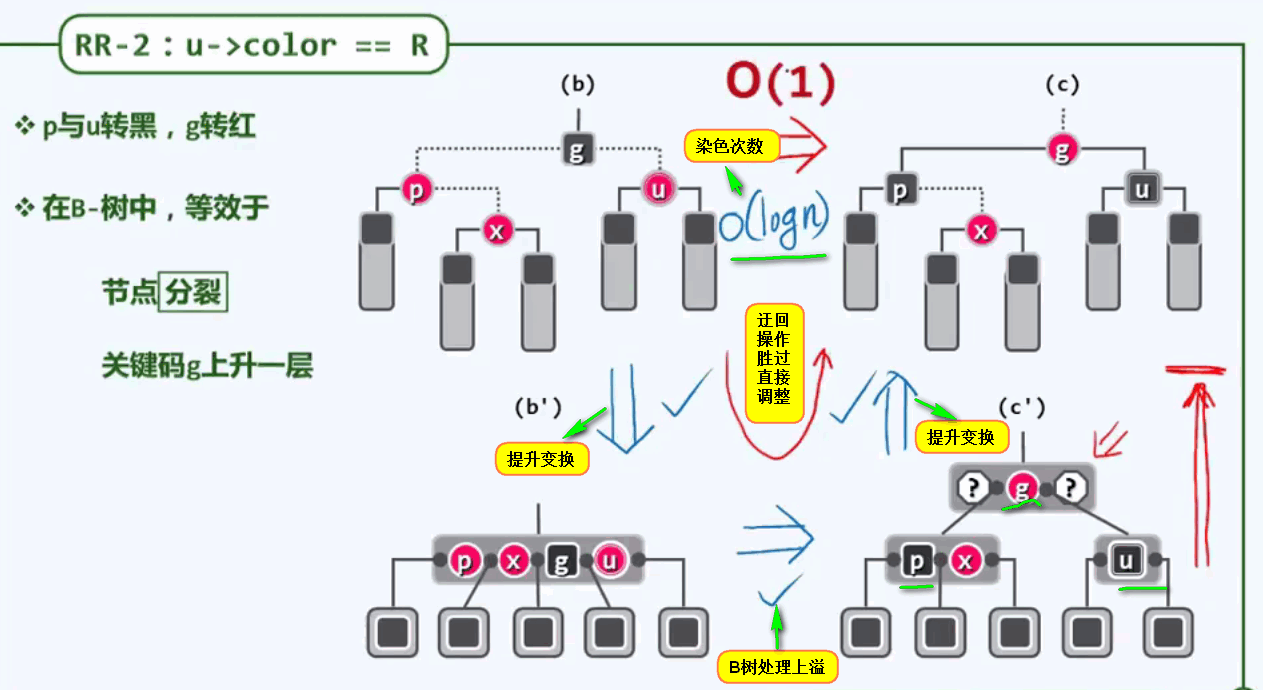
 插入操作讨论：

 

---

 

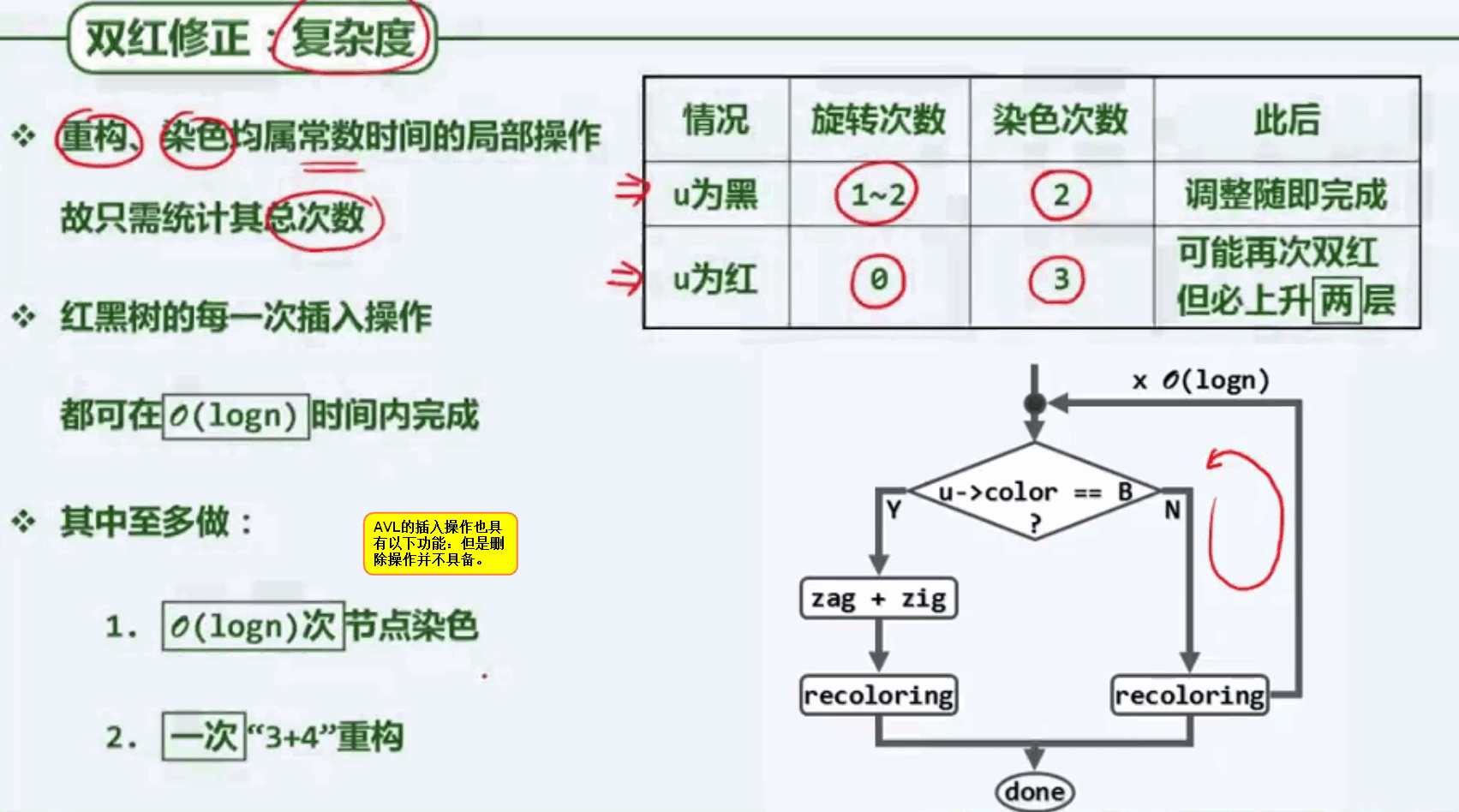
 红黑树的删除算法：

　　

 

 

 

 

 

 

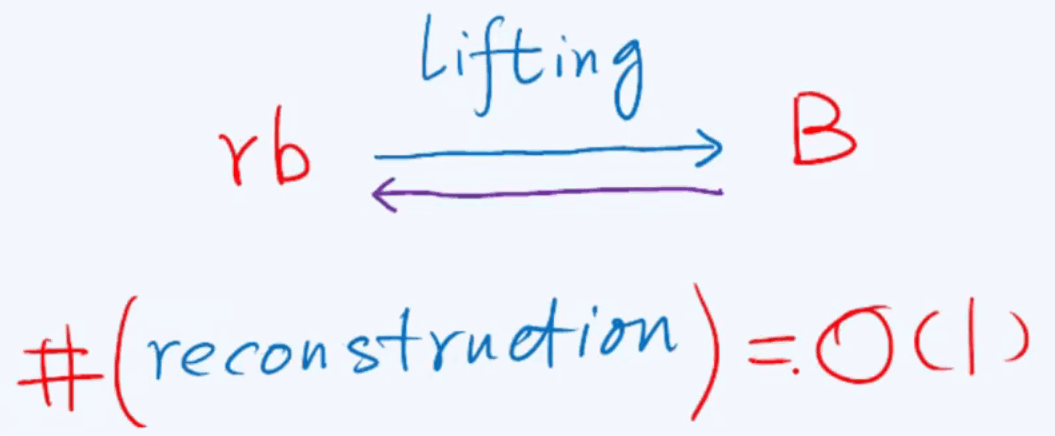
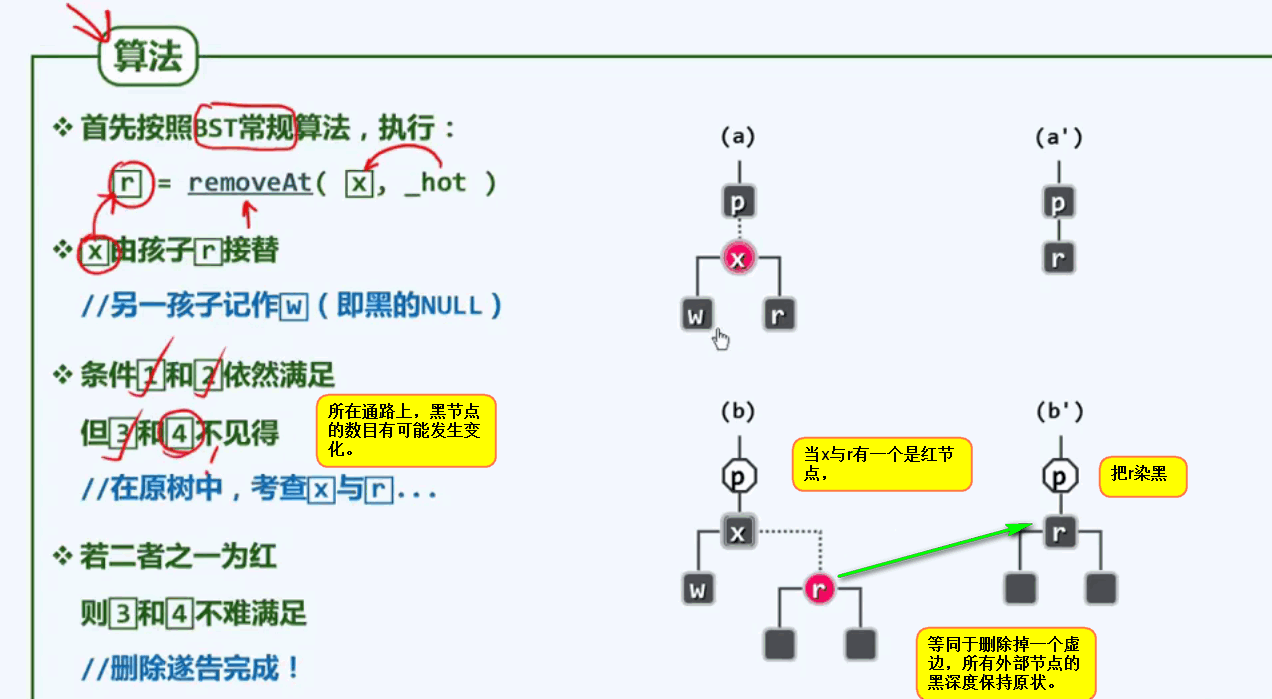
 当待删除节点x与替代者r均为黑色时（双黑）：必然违背第四条规则：

　　

 

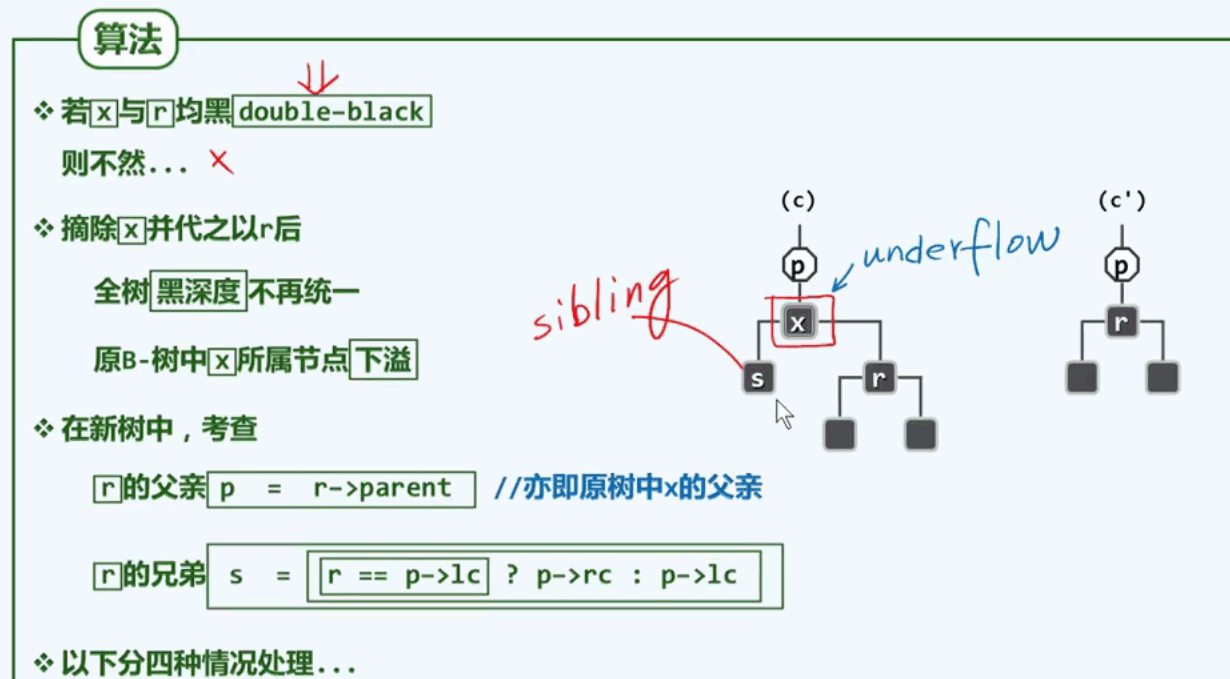
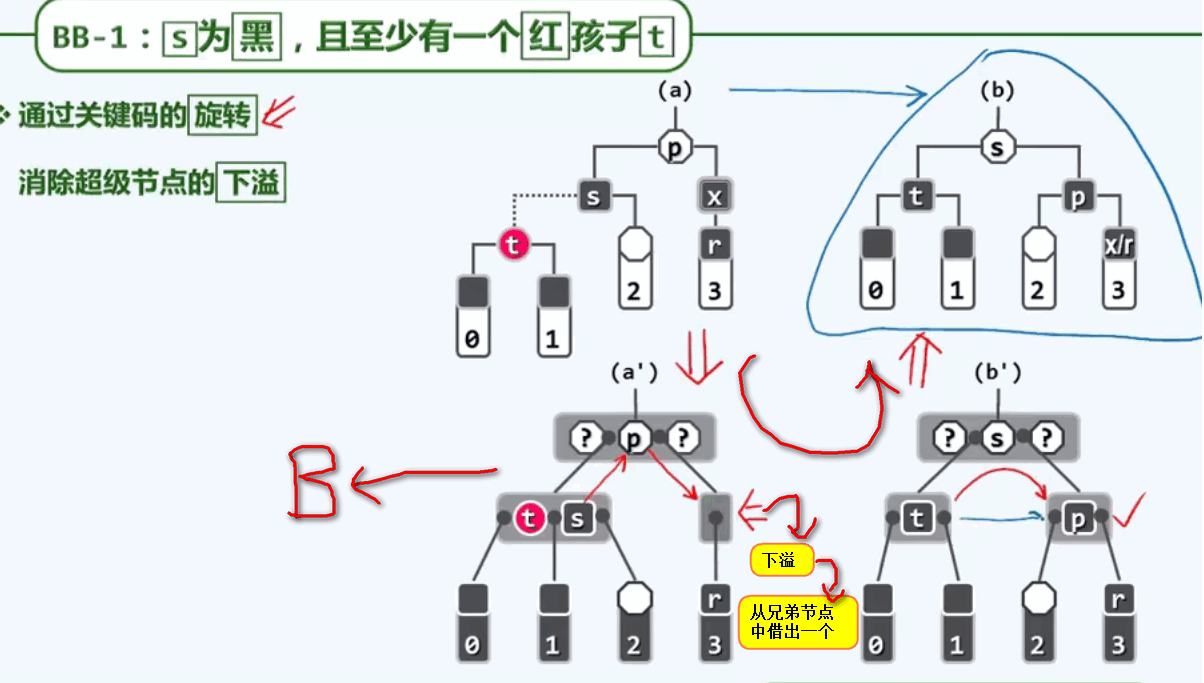
 BB-1：兄弟为黑色，且兄弟s至少有一个红孩子为t.

 

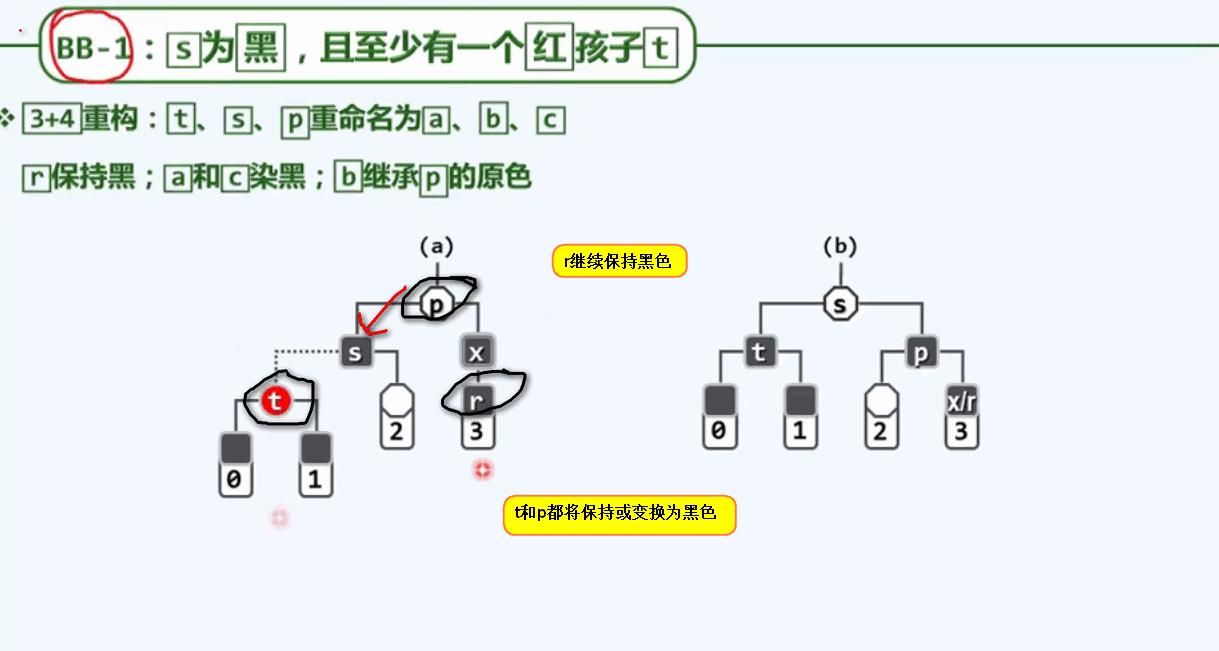
 四颗子树的黑高度都是一样的，如果调整以后，红黑树性质在全局得以恢复——删除完成。这一转换在其背后有着深刻的原理。还是将红黑树转换到B树查看

　

 

 

 

 

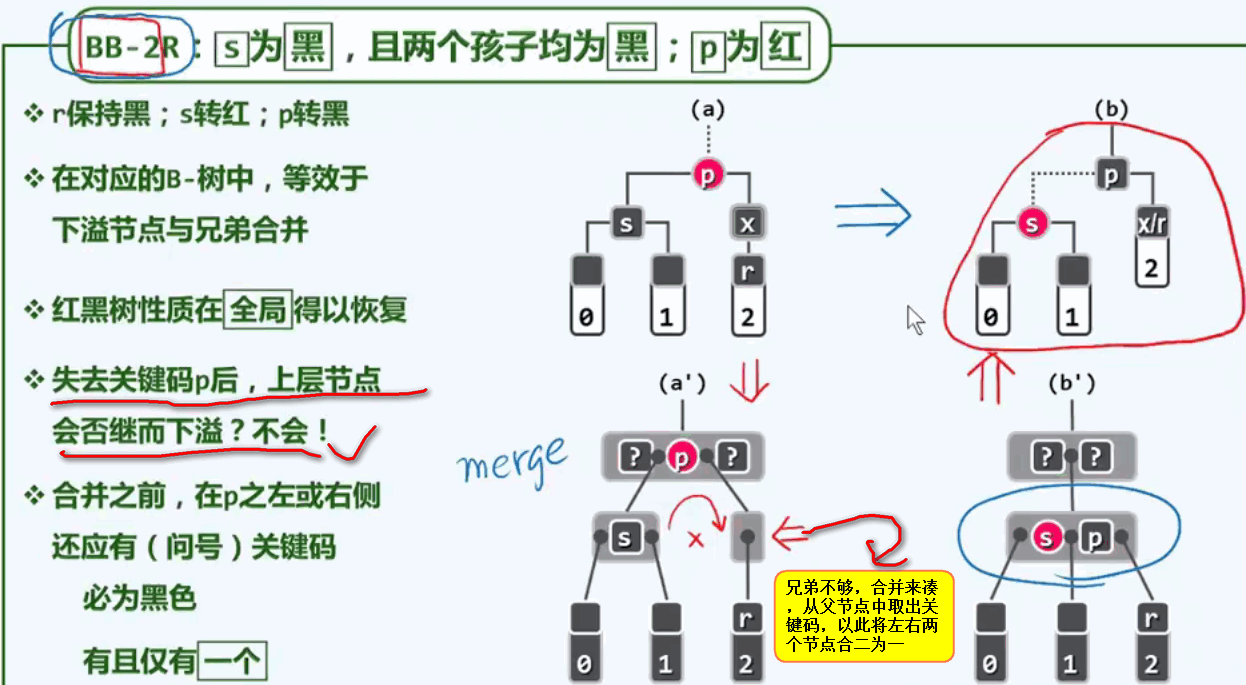
BB2R情况：父亲p为红色，兄弟s及兄弟的两个孩子均为黑色。    而当s的两个孩子都为黑时，提升以后，兄弟节点自己也没有足够的孩子了。

 

 

 

 BB2B情况：父亲p为黑色，兄弟s为黑色，兄弟s的两个孩子也为黑色。

 

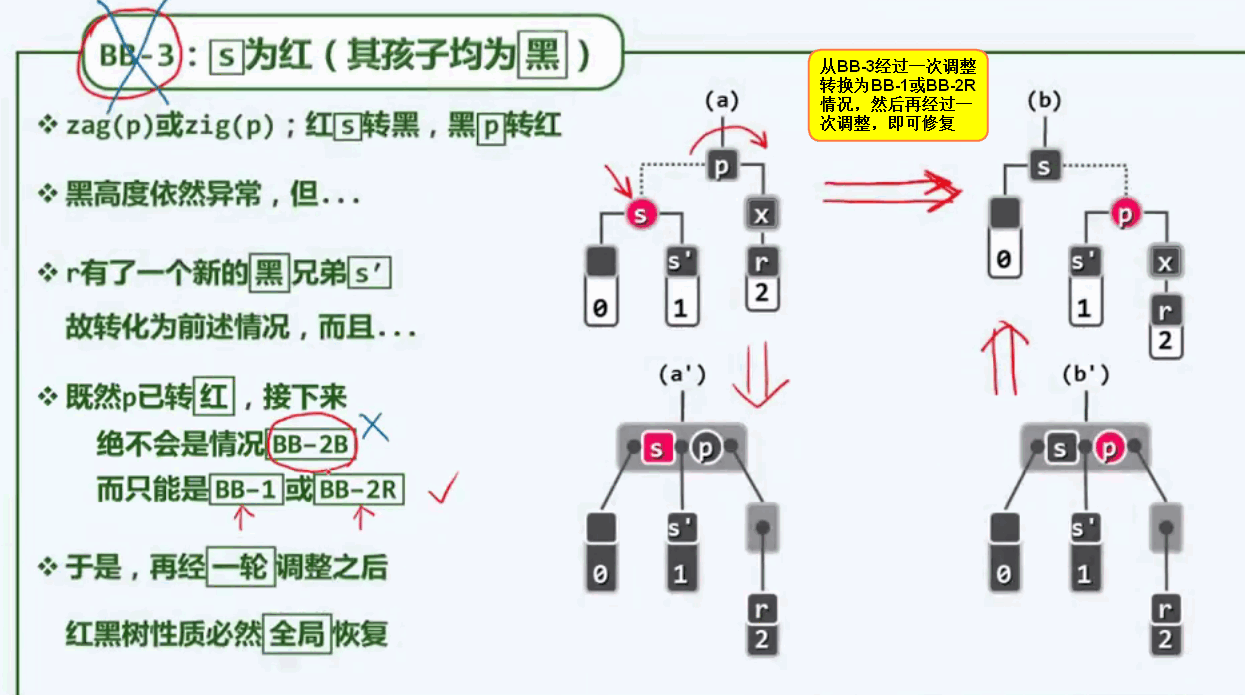
BB-3：兄弟s为红色，其孩子均为黑色

　　　　

 

 

---

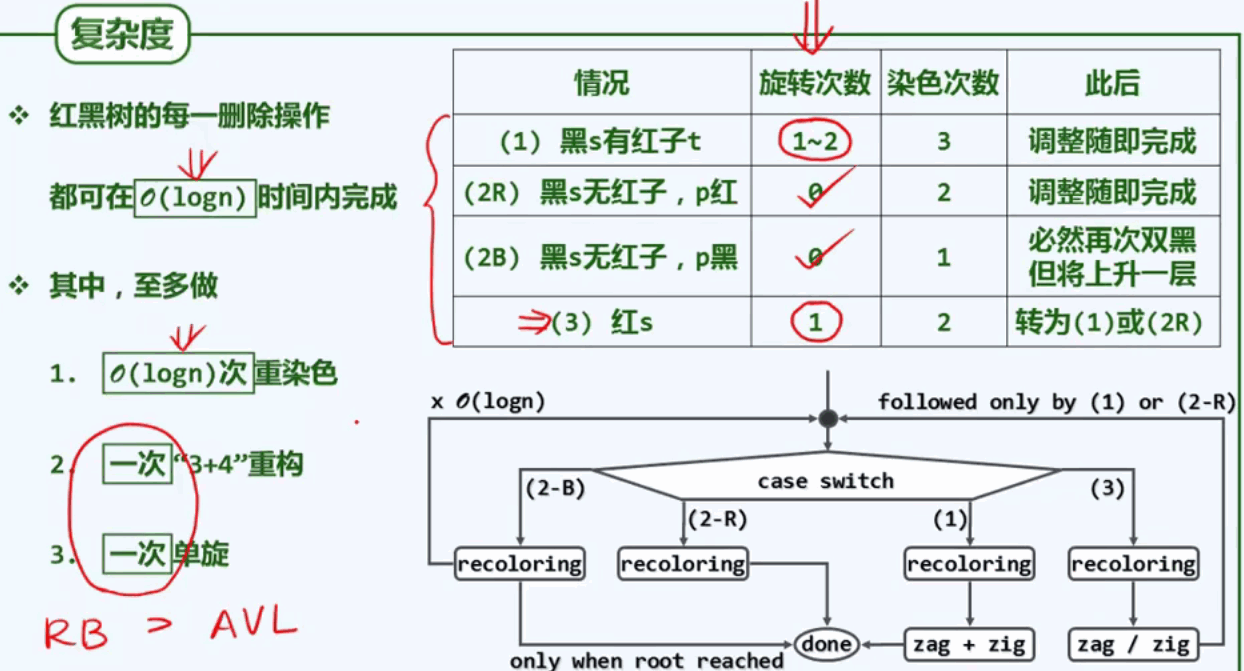
 总结归纳