B-树

一、B-树：有趣且有用

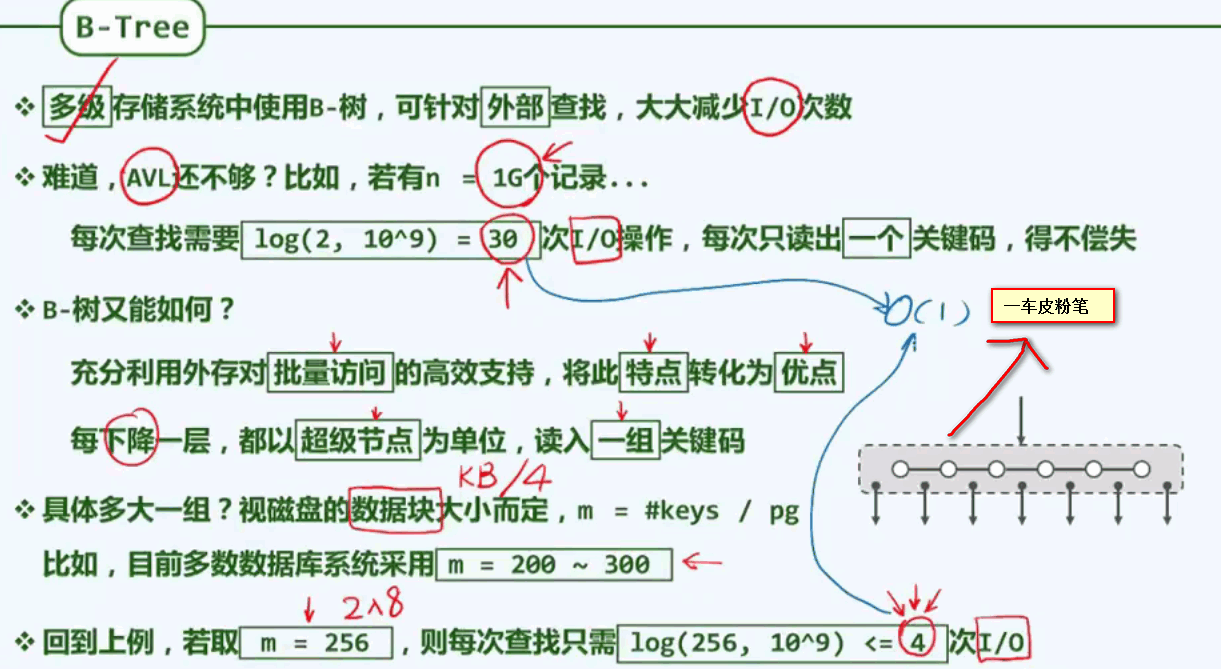
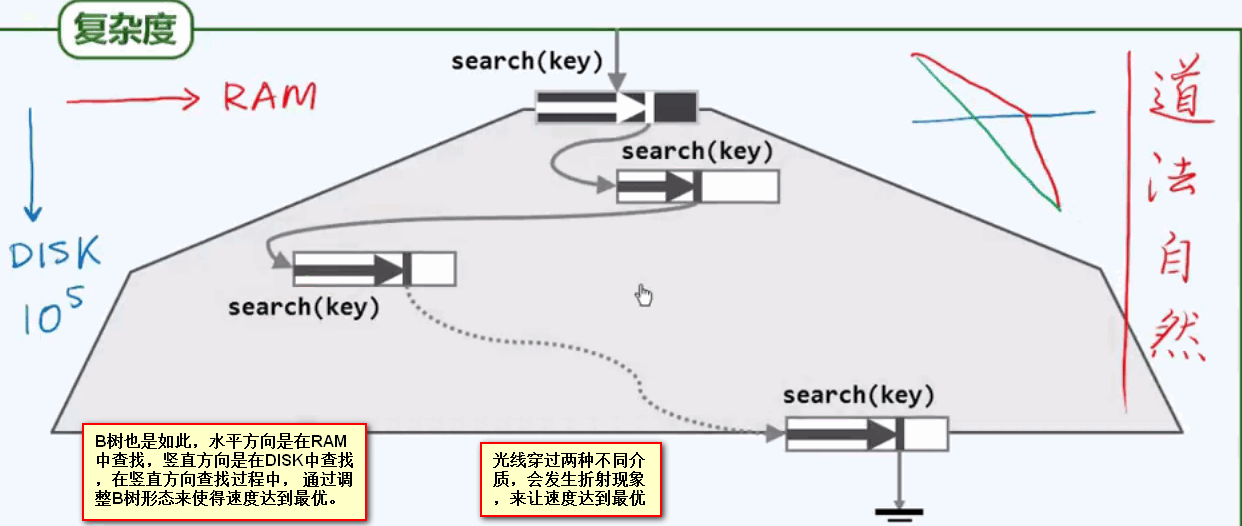
　1.1 设计和实现B-树的动机：　弥合不同存储不同存储级别之间在访问速度上的巨大差异，实现高效的I/O。

 

 

 学完B-树之后会发现比尔盖茨这句短视且武断的话是千真万确的真理？稍后揭晓。

 

  1.2  存储容量增长太慢了

　　

 

 

 

 

 

 

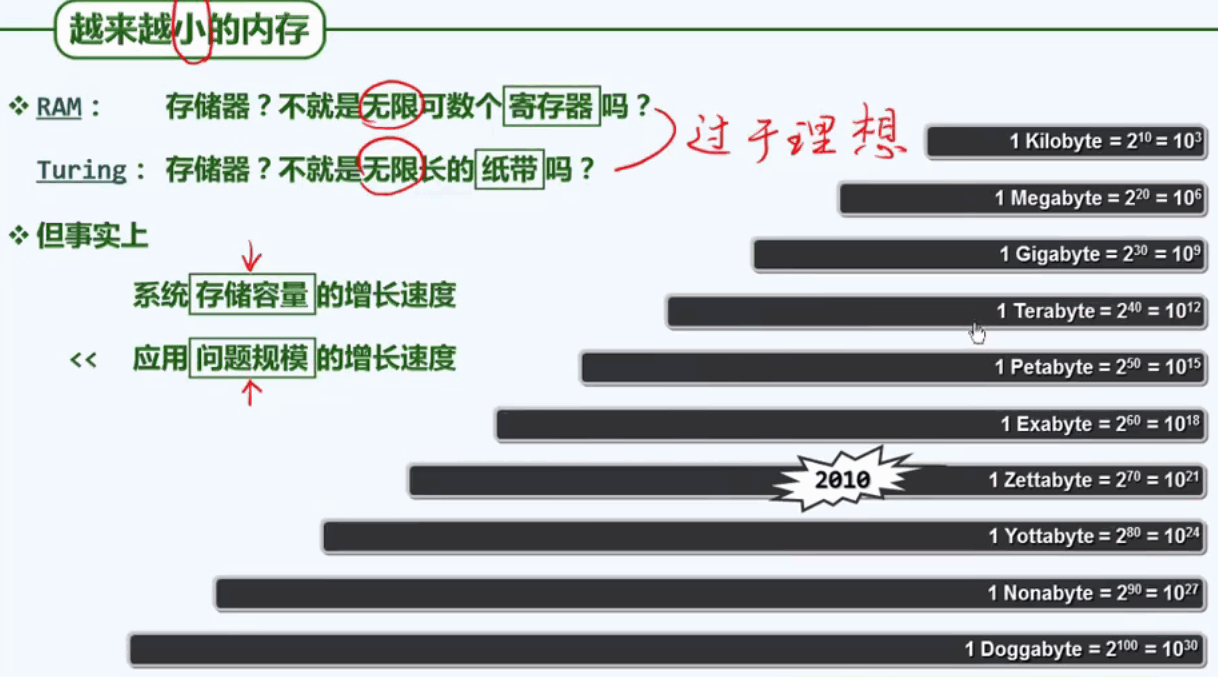
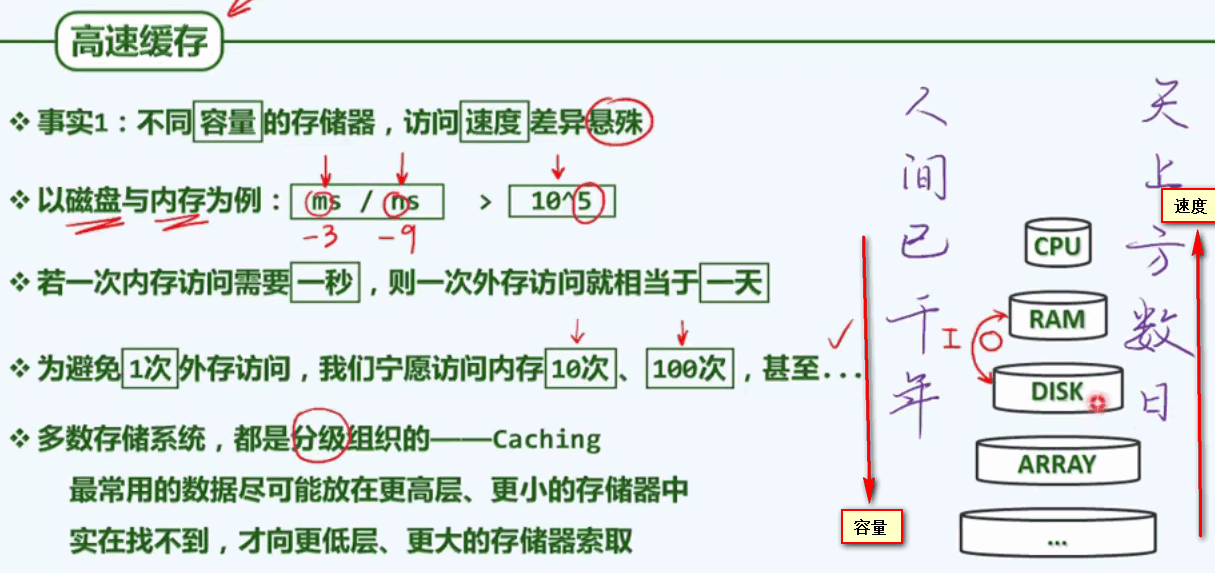
  分级存储是解决需要较多存储器的方法，在由内存与外村组成的二级存储系统之中，数据全集往往存放于外存中，计算过程中则可将内存作为外存的高速缓存，存放最常用数据项的副本。借助高效的调度算法，即可将内存的“高速度”与外存的“大容量”结合起来。

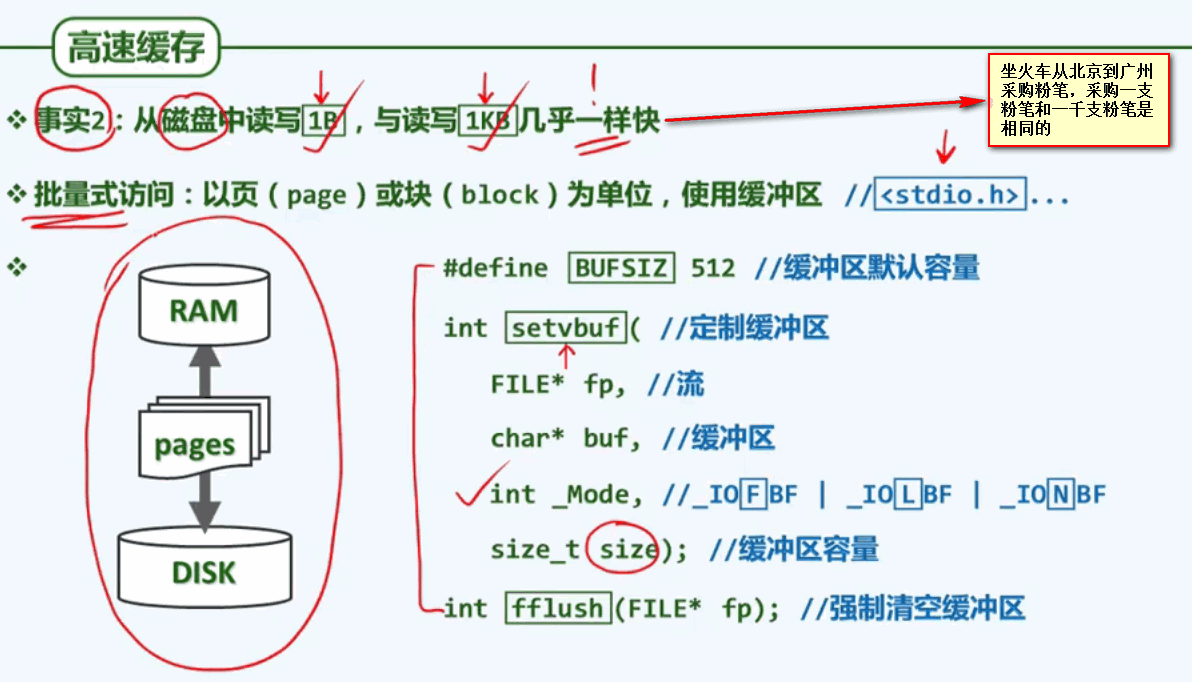
以内存和磁盘为例：其单次访问延迟在ns和ms之间，也就是说对于内存的1秒/1天，相当于磁盘的1周/2000年。所以在衡量算法的相关性能时，我们基本可以忽略对内存的访问，转而更多的关注对外存的访问次数。

 

 

 

 

 

---

 

二、B数的结构：　　

　　每个节点不只是有两个分叉

　　底层高度一致

　　B-树更宽更矮

　　当插入和删除B树的节点时，B树会相应的调整其拓扑结构。

 

 

 

 

 

 

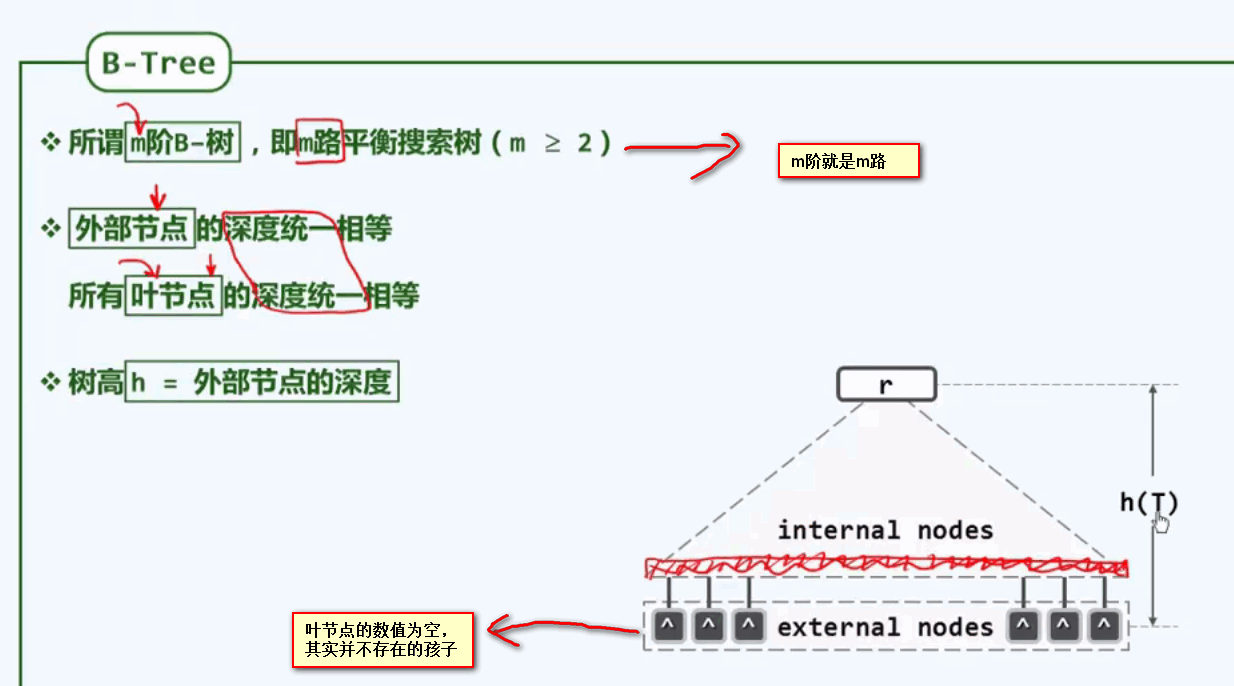
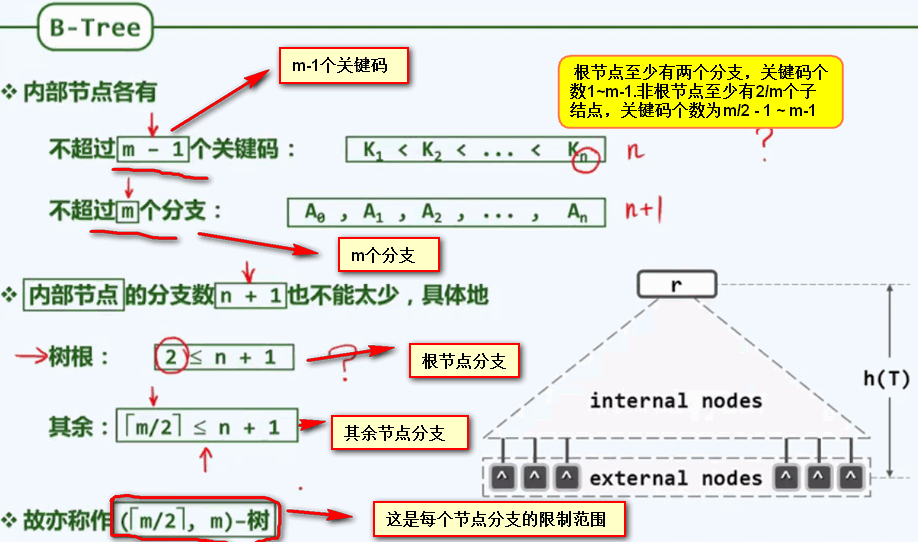
 用超级节点所拥有分支的下限和上限来命名B树，称作([m/2],m)-树。 对于6阶B树，称为（3,6）树；

　

 

 

 

 

 

 

 

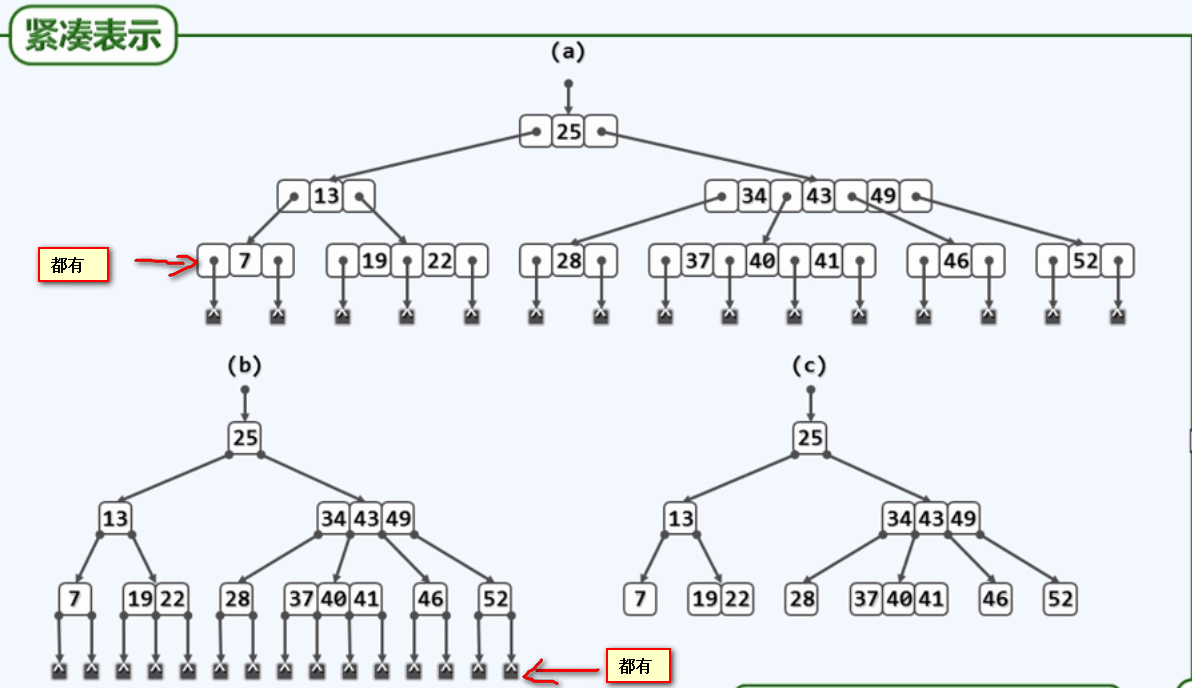
B树的紧凑表示（即使没有画出，B树中也存在很多外部节点和内部引用）：

　　

 

 

 

---

 

三、B树的实现：

　　

 

 

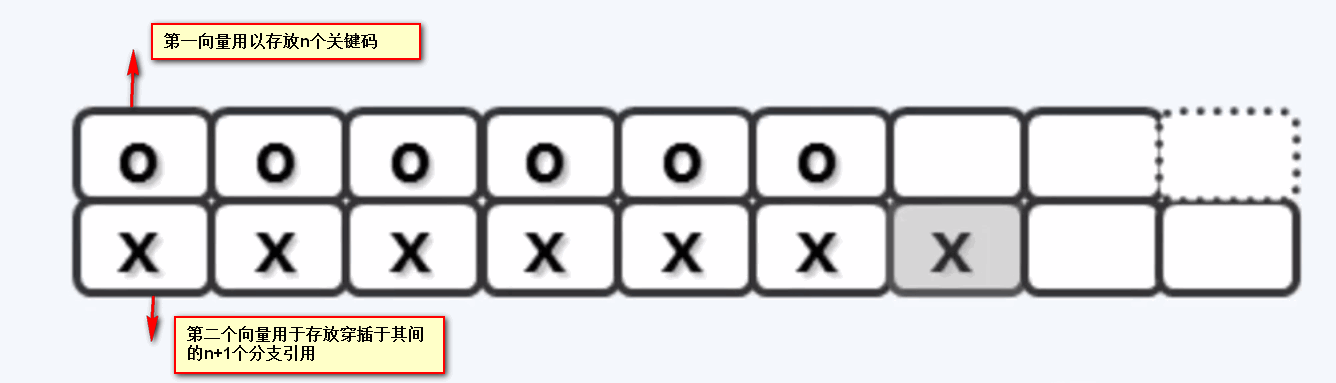
 BTNode的定义：

 

 

 BTree的定义：

　　

 

 

 

---

 

四、B-Tree查找

　　B树的节点众多，以至于节点不能完全容纳在内存中（甚至内存完全不容纳），所以B树的查找诀窍是：只需要将必须的若干节点载入内存，只载入必须的节点，尽可能的减少I/O操作。

　　根节点常驻内存：单个节点查找的时间复杂度为O(1)，因为它是由vector构成的，属于线性结构，查找需要线性时间。

　　

 

 

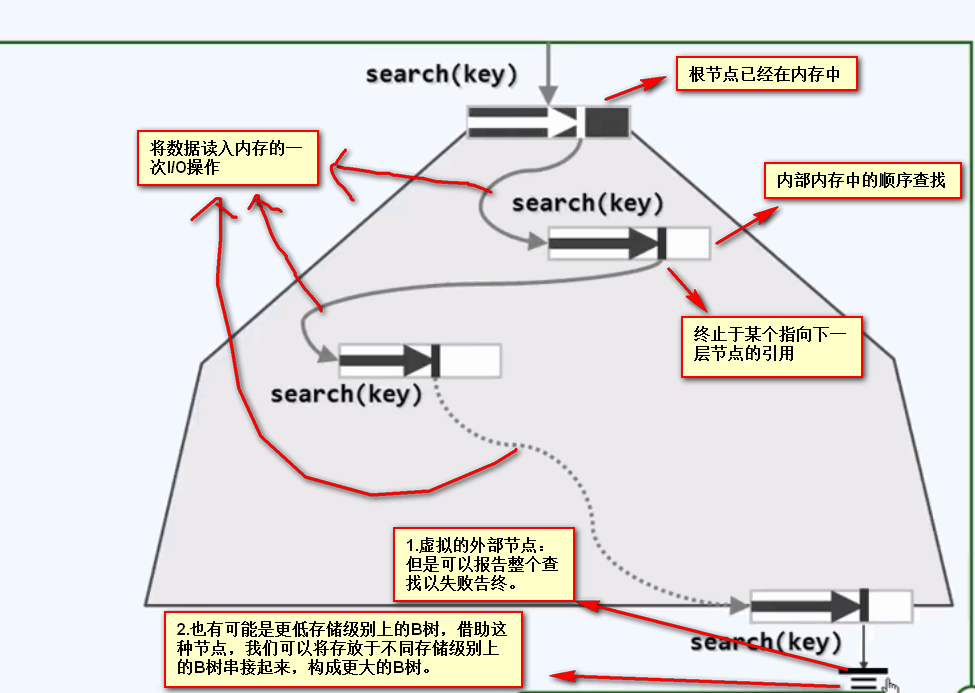
 成功查找实例：

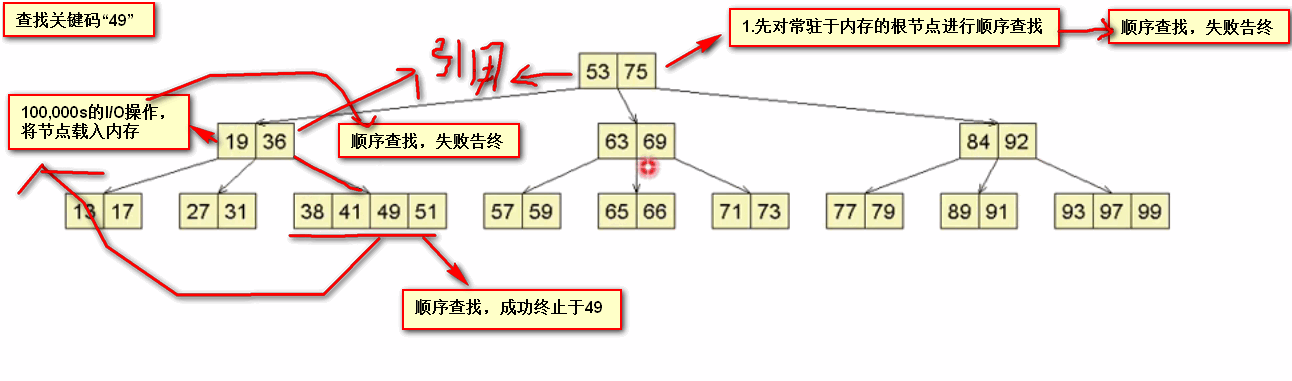　　失败查找实例：

 

 

 

 

---

 

查找算法的代码实现：

　　

 

 

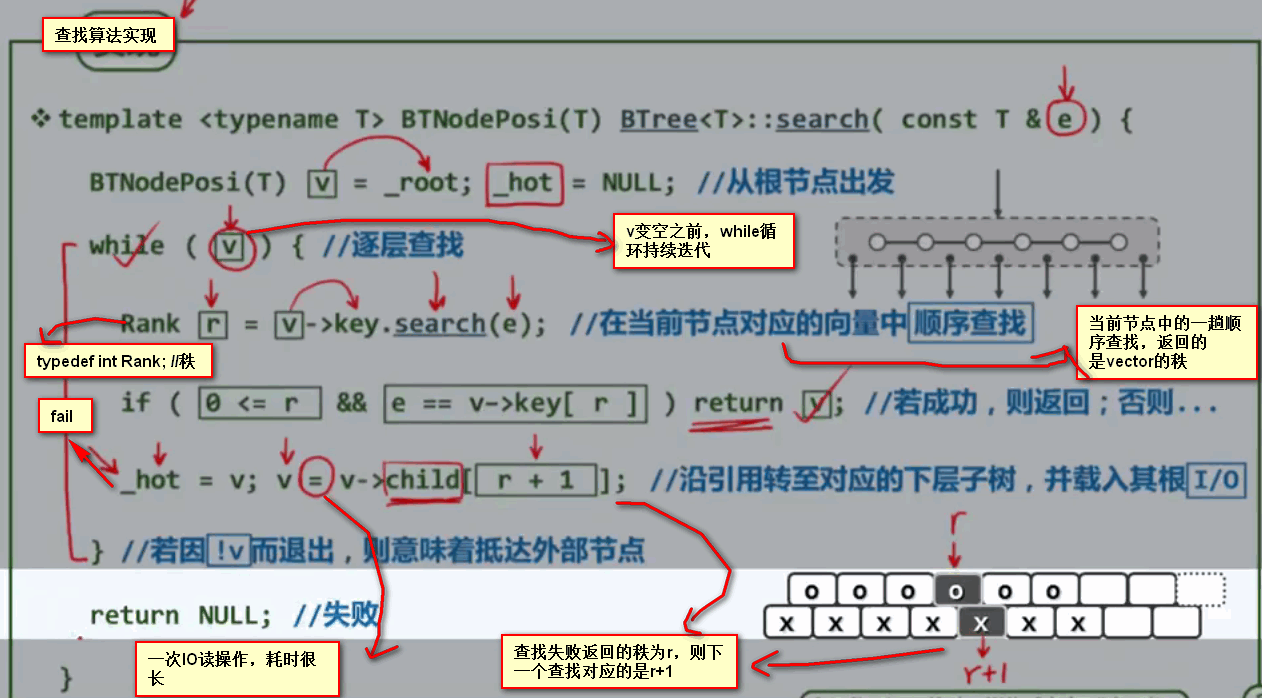
 B树查找算法的复杂度：

　　

 

 

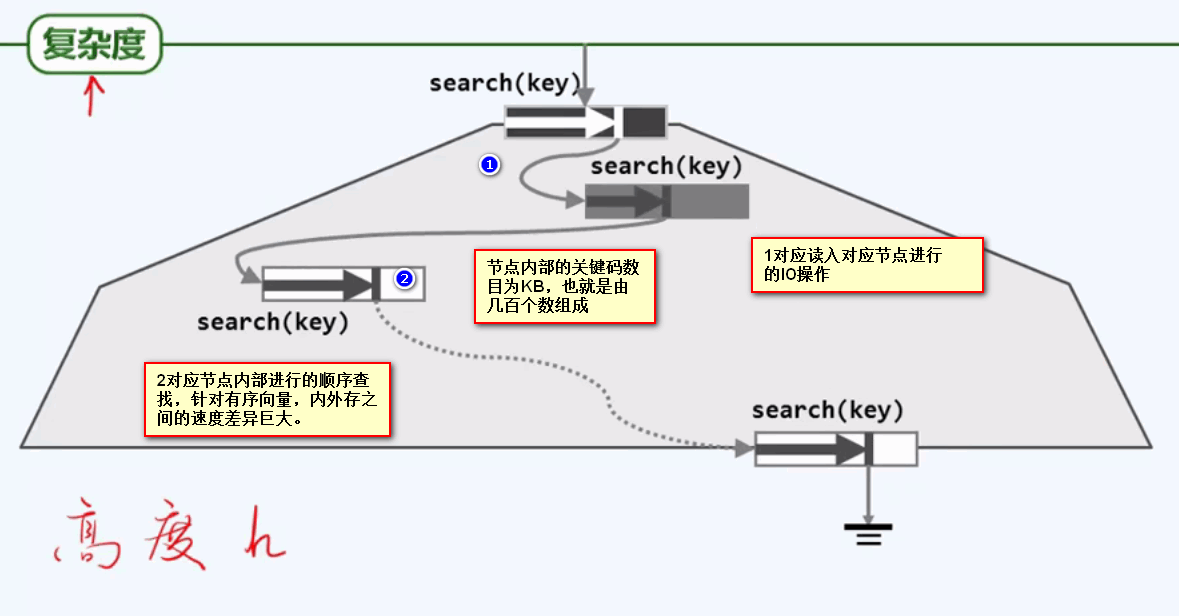
 所以查找的复杂度由B树的高度h决定的：

下面来看下B树的最大高度是多少：

　　

 

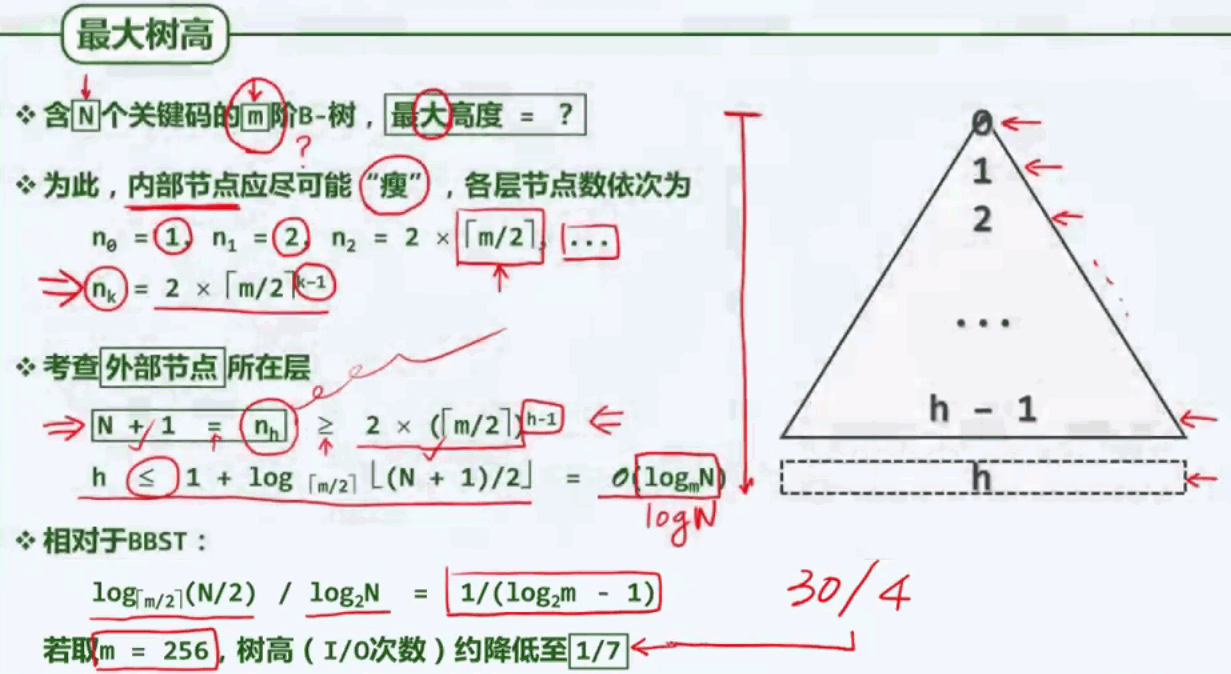
 下面再来看看B树的最小高度：

　　

 

 

---

 

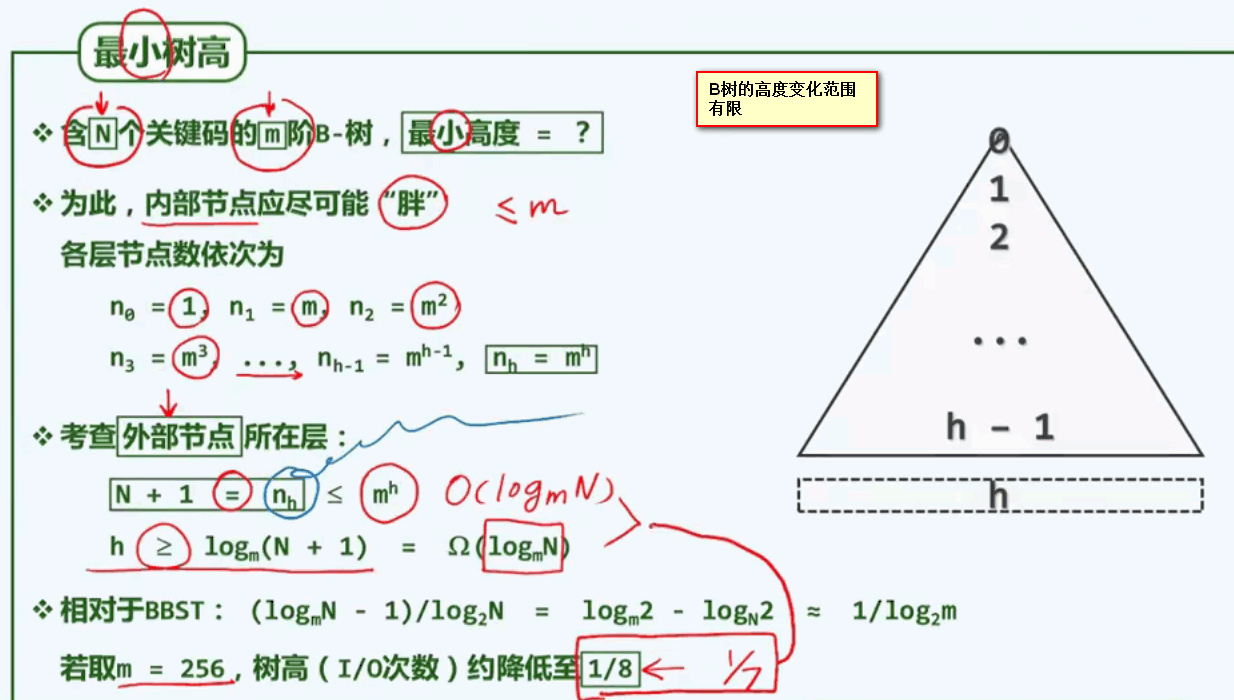
五、B树的插入操作：

　　　

 

 分裂处理：

　

 

 

 

 

 

 

---

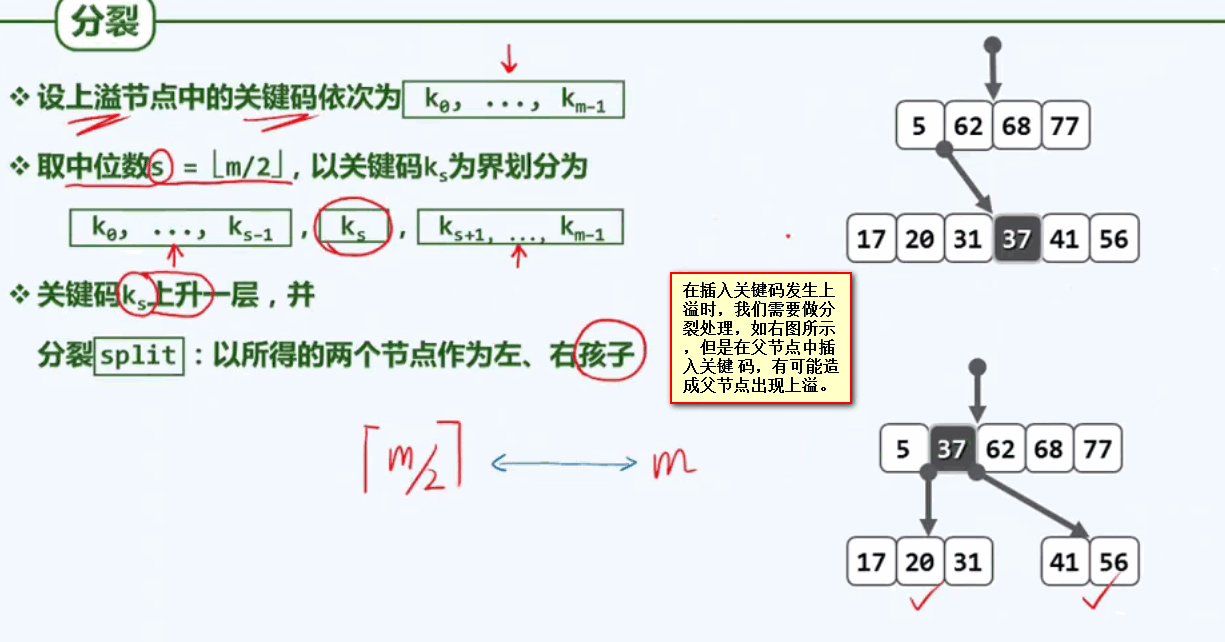
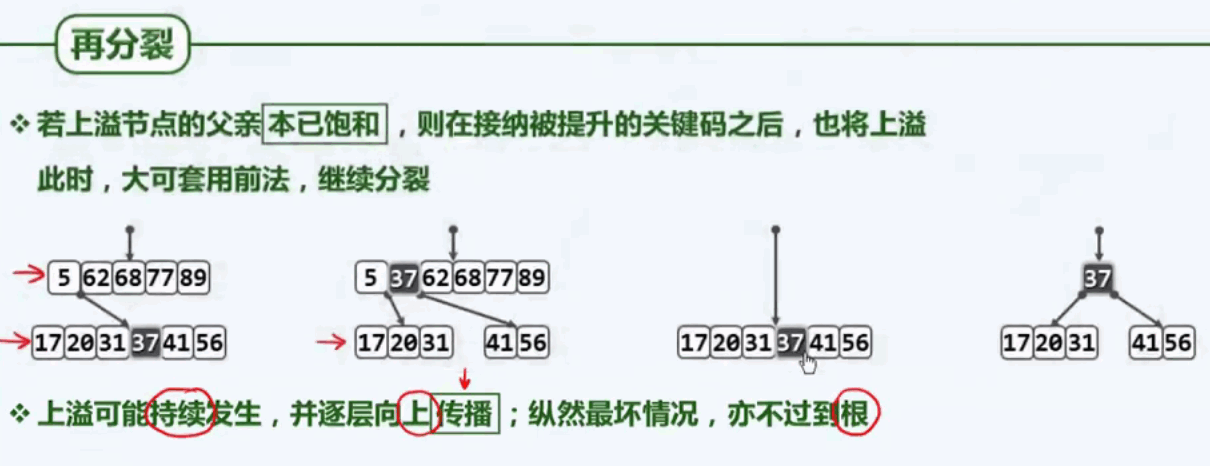
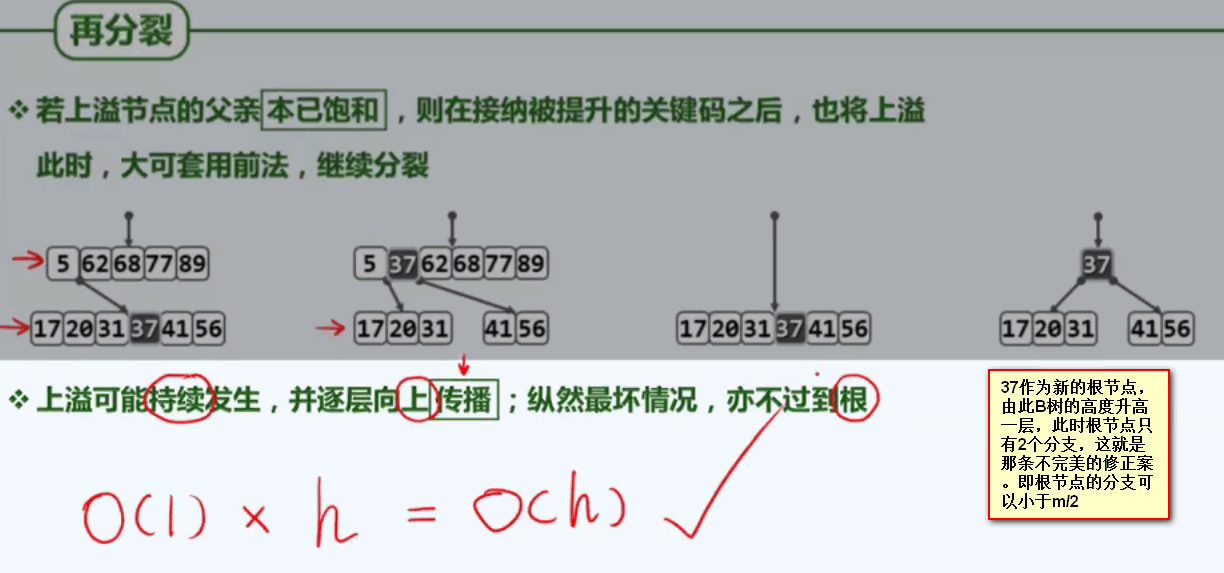
 六、B树的删除操作：

　　

6.1.当删除节点造成某一个节点发生下溢：（此时下溢节点v的兄弟有足够的关键码可以曲线借出） 则使用旋转操作

 

 

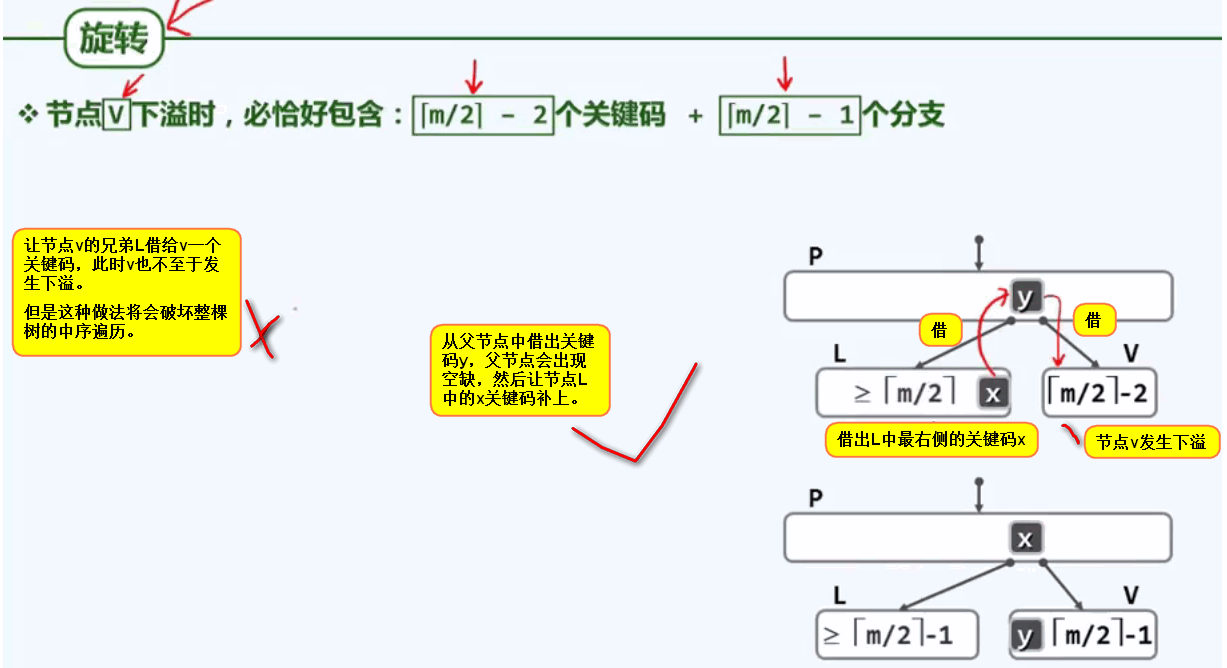
 6.2.发生下溢后，左顾右盼，发现L或R根本不存在，又或者所含的关键码均不足m/2个：则使用合并操作

　　　　

 

 6.3 B-Tree删除操作示例演示1：

　　　

 

 

 

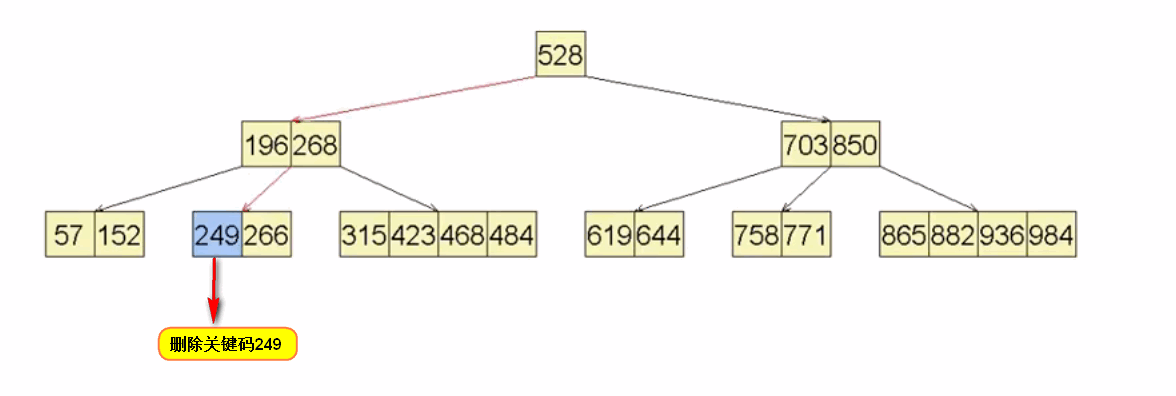
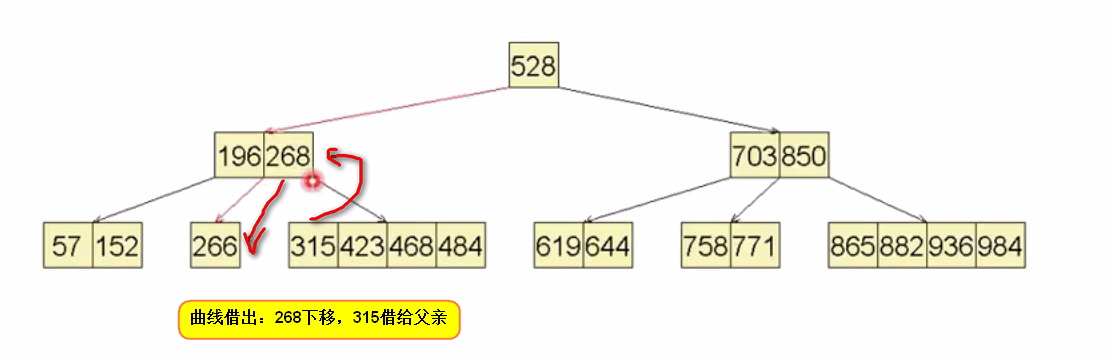
 至此删除操作完成。

 

 6.3 B-Tree删除操作示例演示2：

 

 

 

 

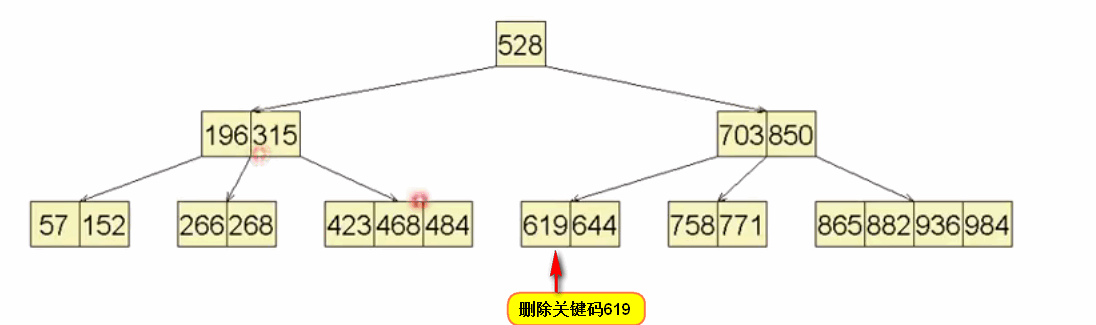
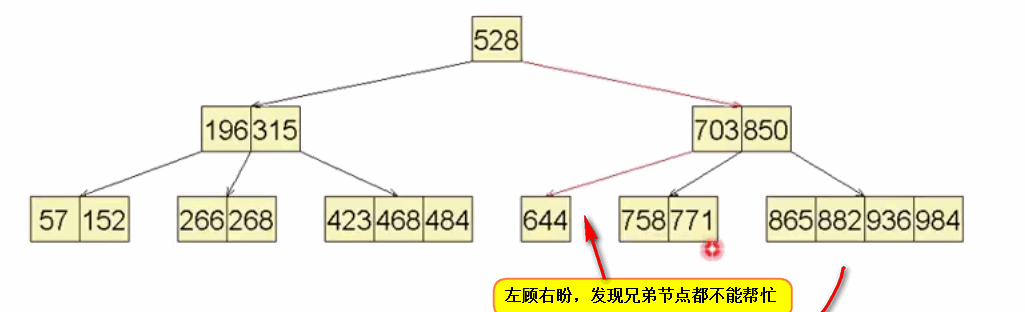
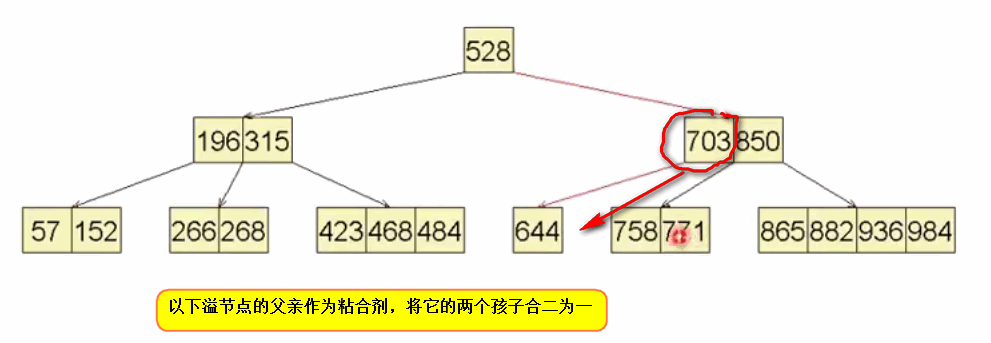
虽然下溢节点得到了修复，但是随即父节点也发生了下溢：如下所示

 　　

 

 

 

 

---

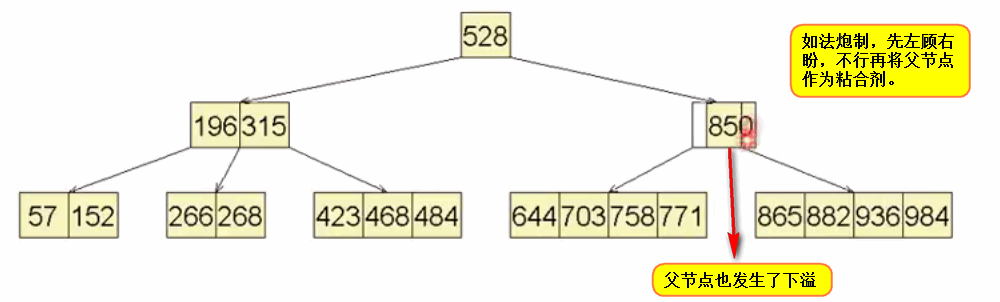
 七、B树总结：

　　对B树的访问无非是使用一些列的对内存和外存的操作完成，外存操作的代价与内存操作的代价大致相当。