AVL树

 AVL树

　　

 

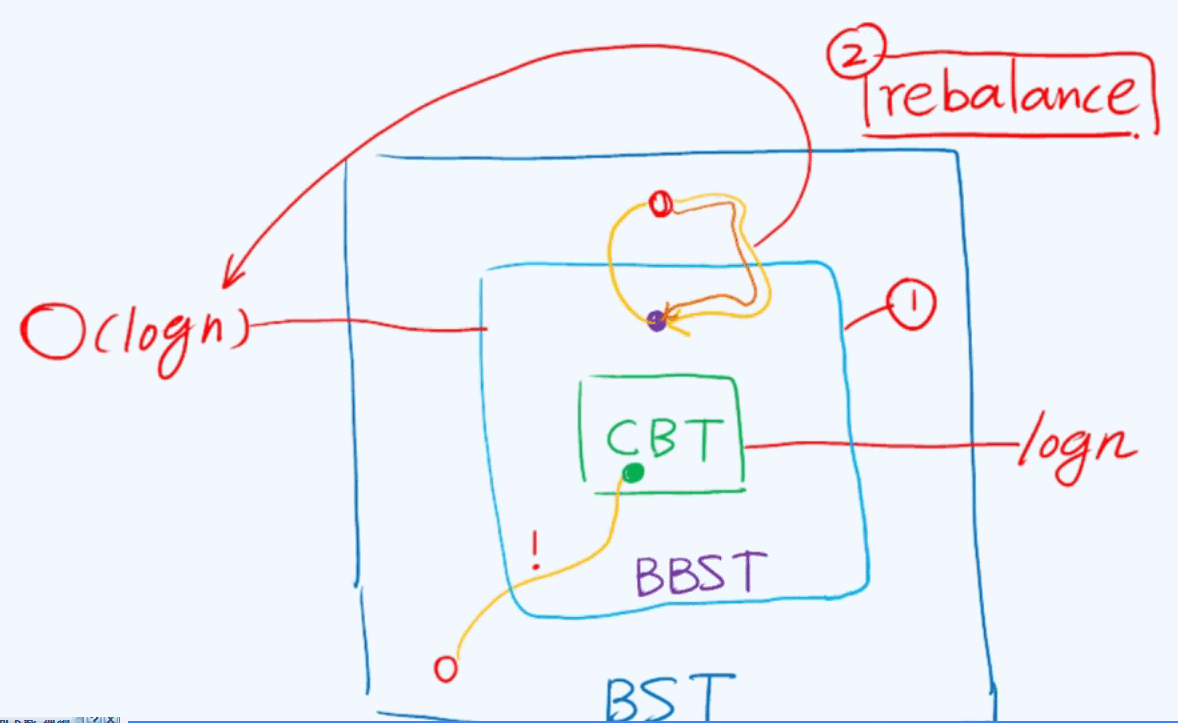
 如何判断平衡？

　　在AVL的意义下的适度平衡，凭借什么判断一颗树是在AVL意义下的平衡。

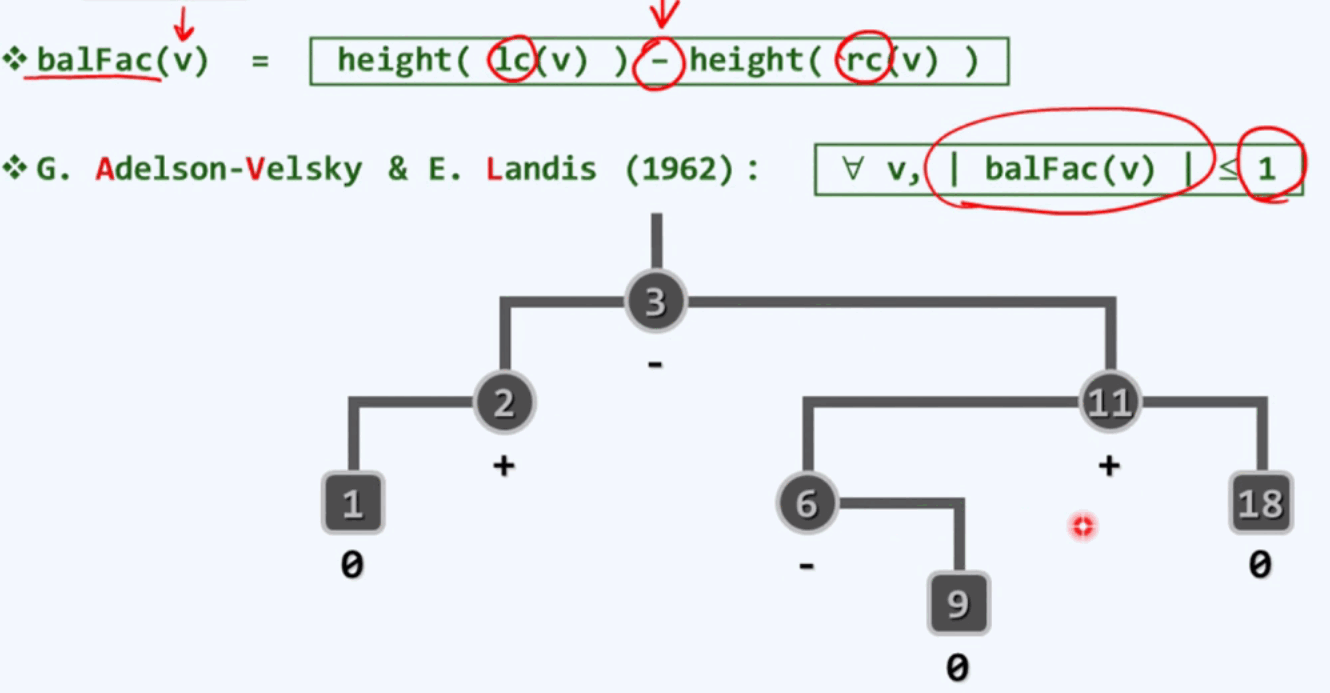
　　平衡因子

 

 AVL的节点个数与树的高度满足以下两种关系：　　

 

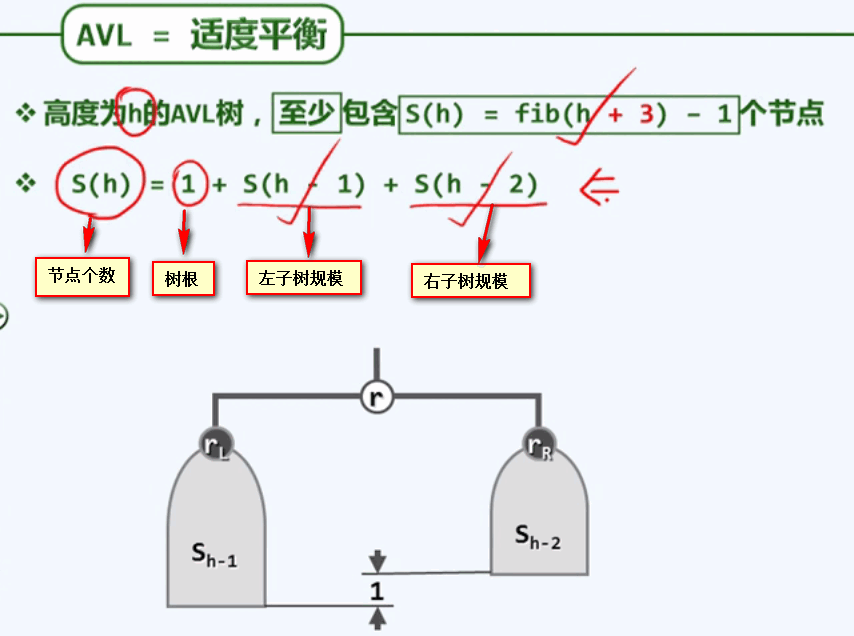
 进一步变形：

　　

 

 

　　AVL树的接口：

　　

 

 

　　AVL树新插入一个节点，只可能导致新插入节点的若干个祖先失衡，而不会导致非祖先的其它节点失衡。其原因在于，对于非插入节点祖先的节点来说，它们和它们孩子的高度都不会发生变化。如果此前是平衡的，那么它们就不会变成失衡。

　　对于删除操作，至多只有一个节点导致失衡。如果删除一个节点导致失衡，则祖先的高度并不会变化。

　　

 

 

但是插入操作至少是一个好孩子，它有可能在某个时候床下一连串的祸，但是它会痛改前非，只要改成其中一个错误，其他的错误就会烟消云散。

删除操作，每次只会闯下一个错，但是当你帮它改正一个错后，它转眼之间有可能再会犯下另一个错误。

实际上插入操作更为简便。

 

---

 

 AVL的插入：

　　zagzag情况：      全部朝右

　　zigzig情况：       全部朝左

　　

 

 

 插入算法的代码实现：

　　

 

 AVL树删除算法：

　　

 

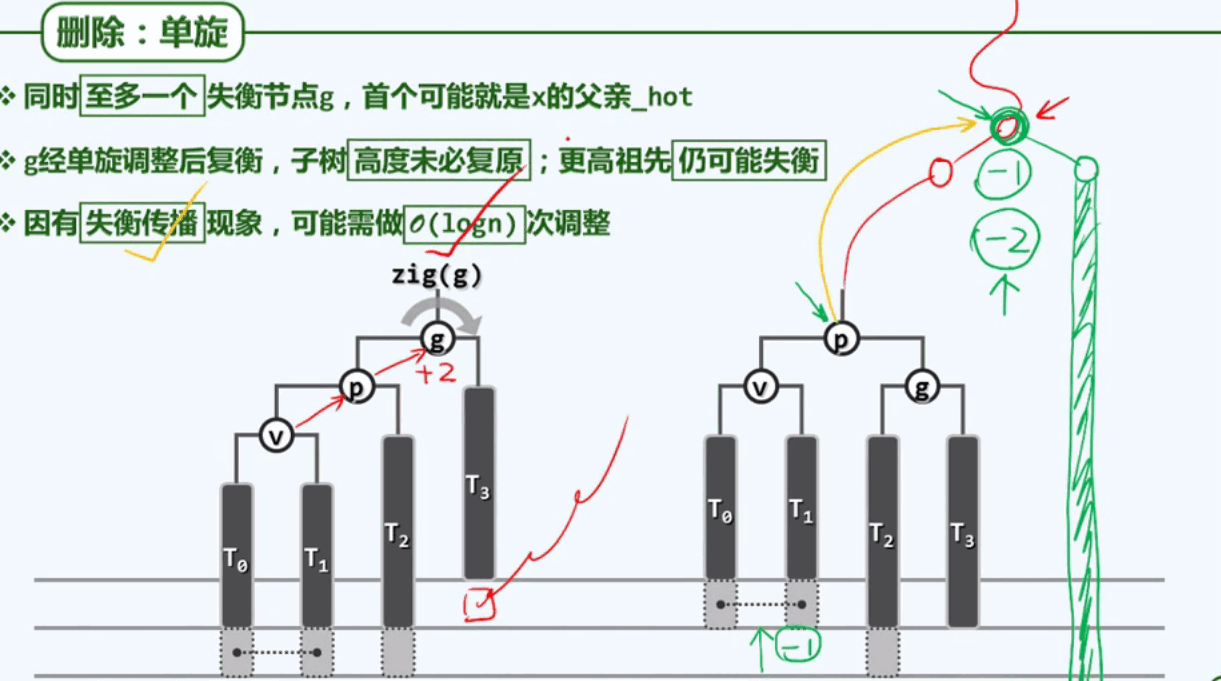
 有可能经过logn次的向上旋转调整：

 

 

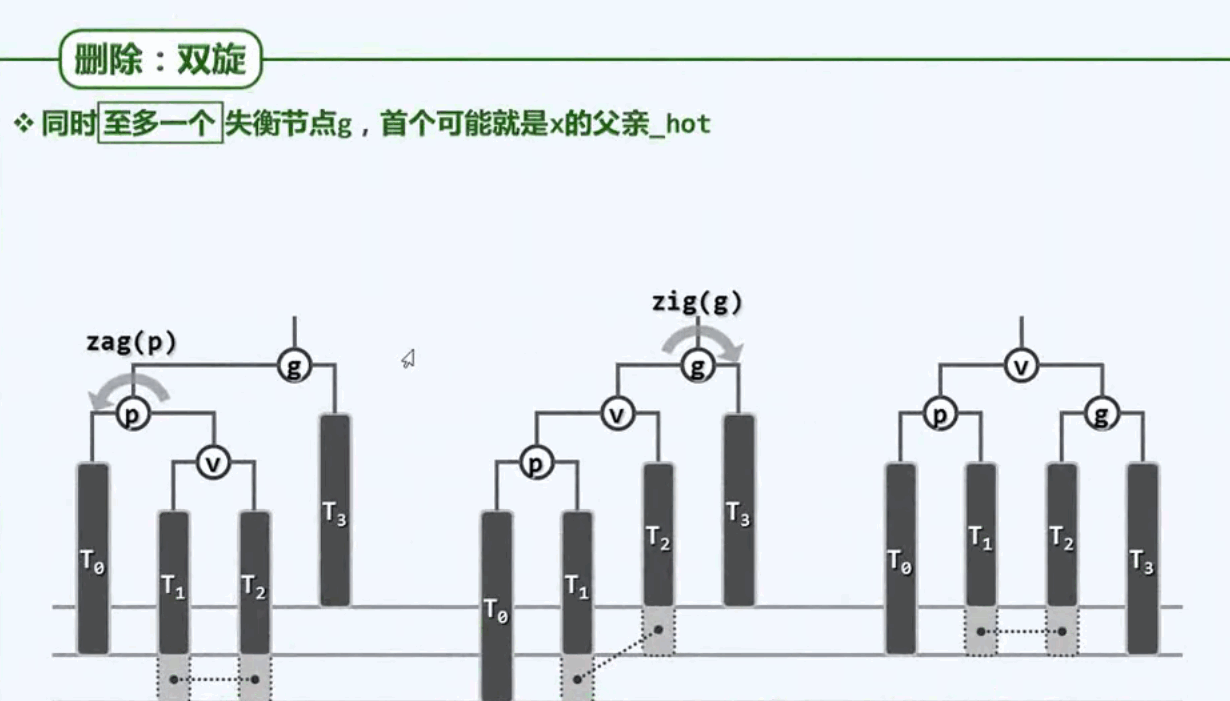
 具体实现代码：

　　

 

 

 

 

 

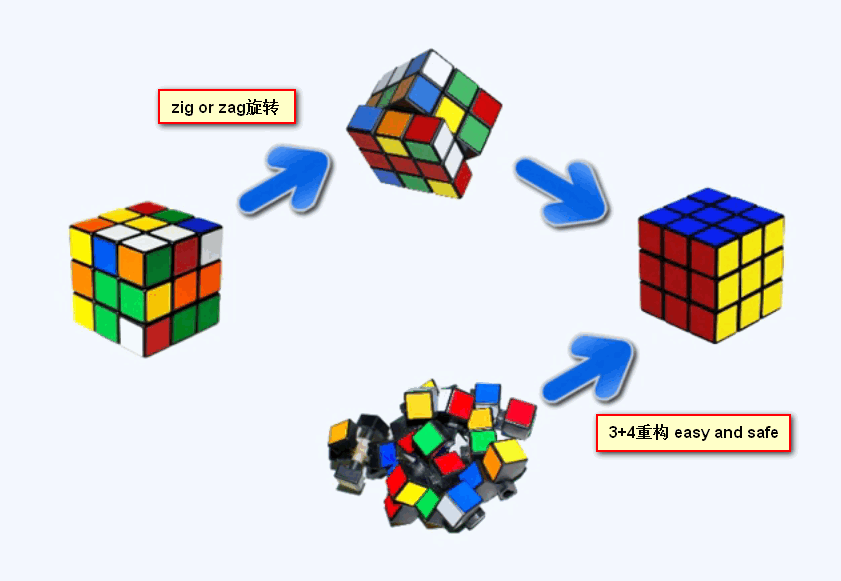
 zig-zag旋转采用玩魔方算法：无论你初始的状态如何，经过一些列旋转最终要达到以下状态：即3+4重构。

　　

 

 

 

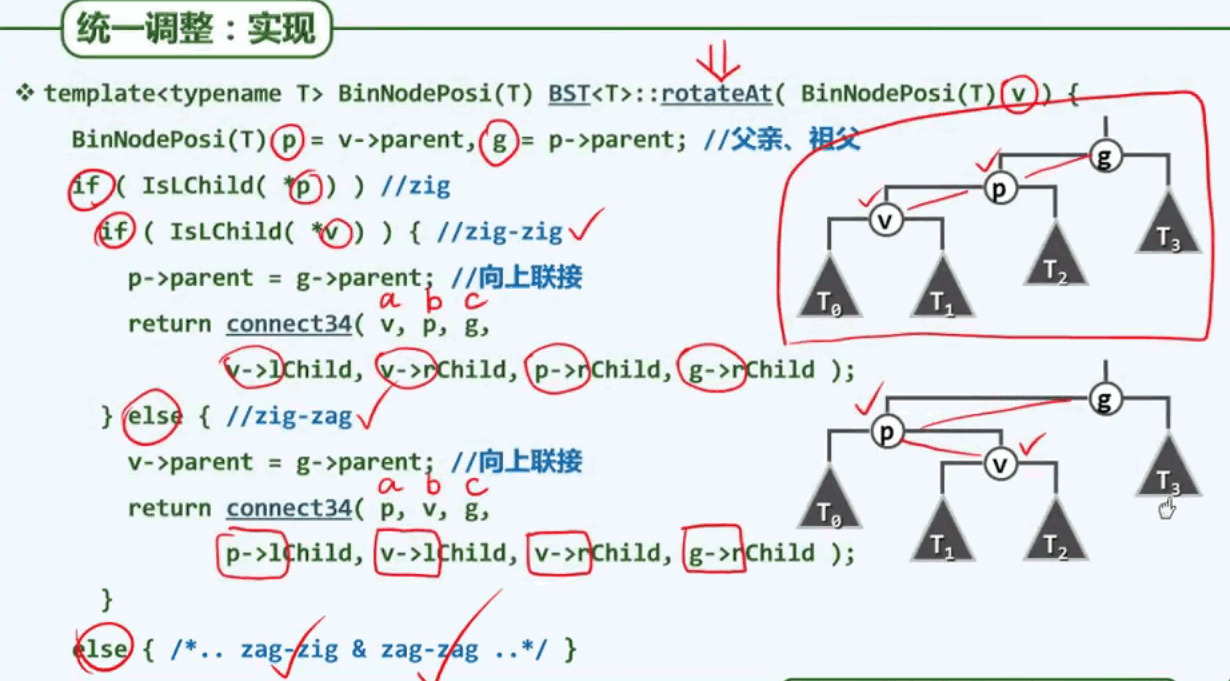
 3+4的重构实现：

　　

 

 

 

 

 

 

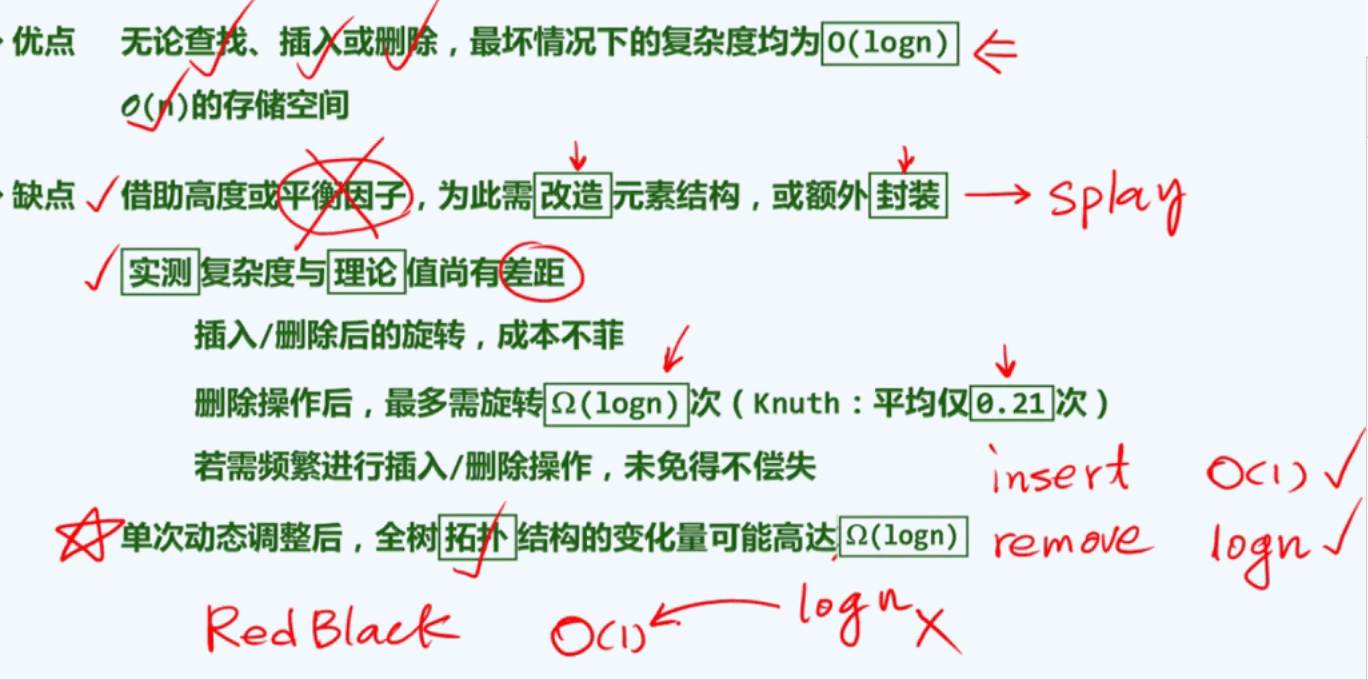
 AVL的综合评价：