二叉搜索树(Binary Search Tree)
二叉搜索树
若既要求对象集合的组成可以高效率的动态调整,同时也要求能够高效率的查找。
通过对二分查找策略的抽象与推广,定义并实现二叉搜索树结构,基于半线性的树形结构,正是后续内容的立足点和出发点。
二叉搜索树为我们同时实现高效的静态操作以及动态操作提供了基础。


将Binary Search Tree称为BST. BST与其他BT有什么不同呢?概括起来就是处处满足顺序性:
任一节点均不小于/不大于/其左/右后代。
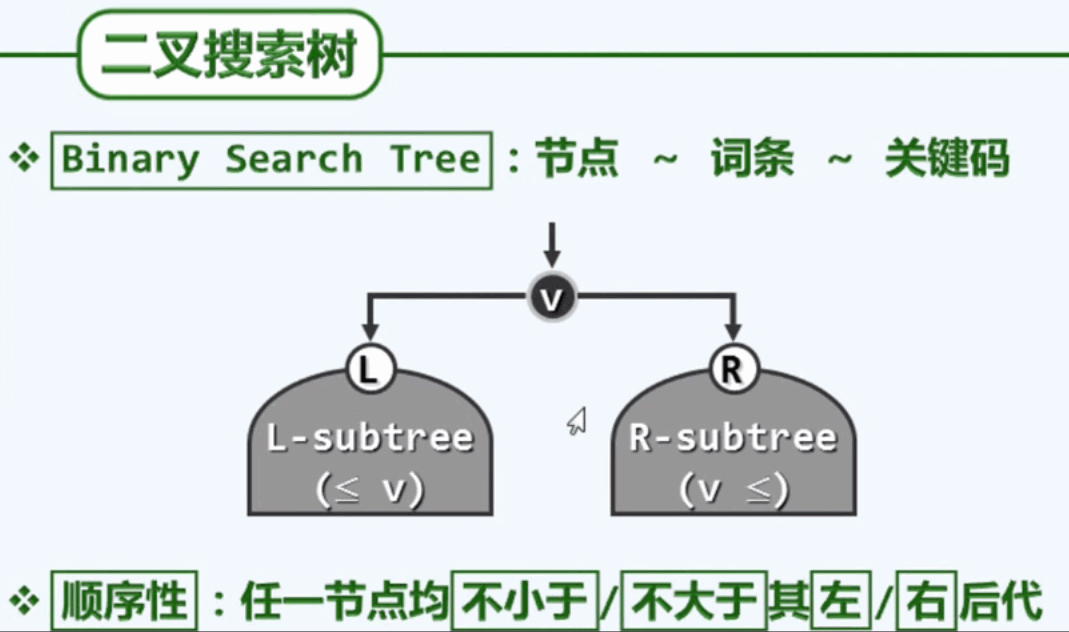
BST的中序遍历必然是单调非降:在微观上处处满足顺序性,在宏观上整体满足单调性。
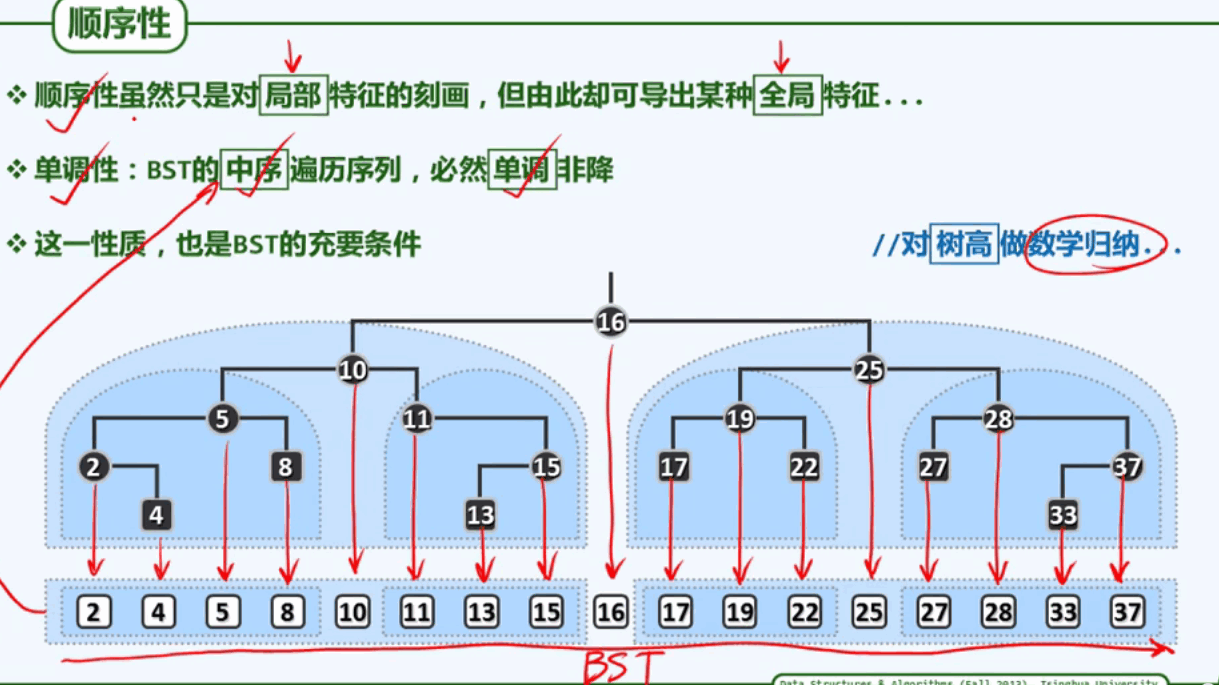
BST模板类:
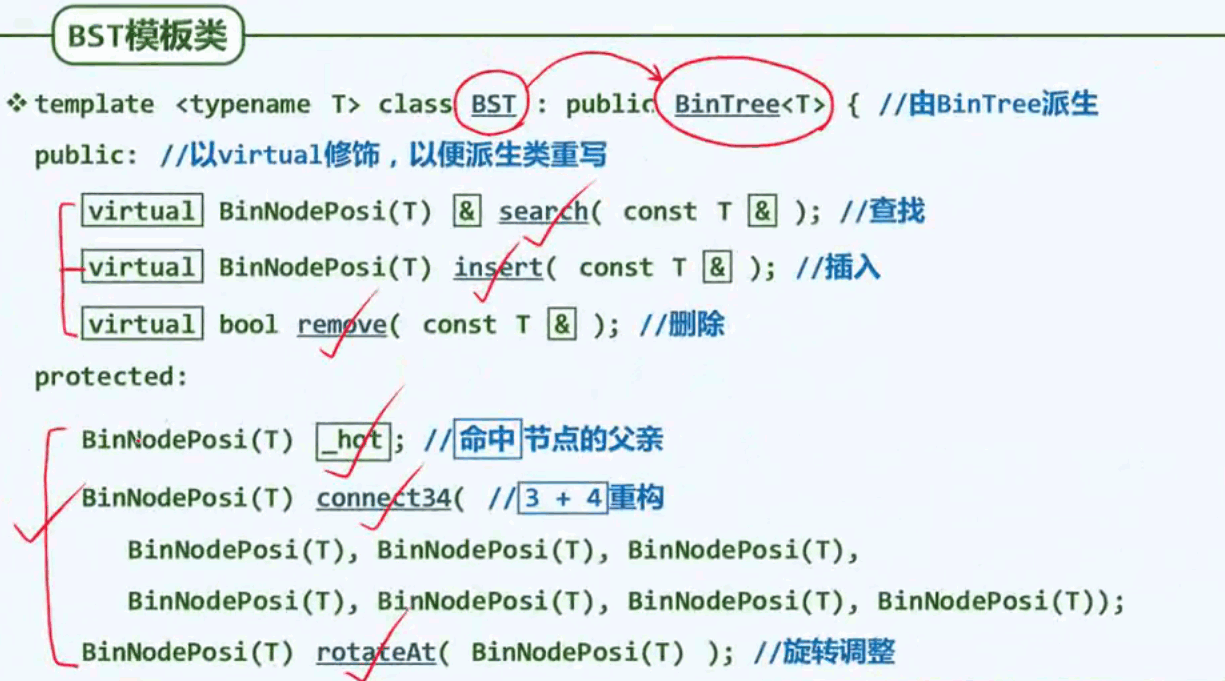
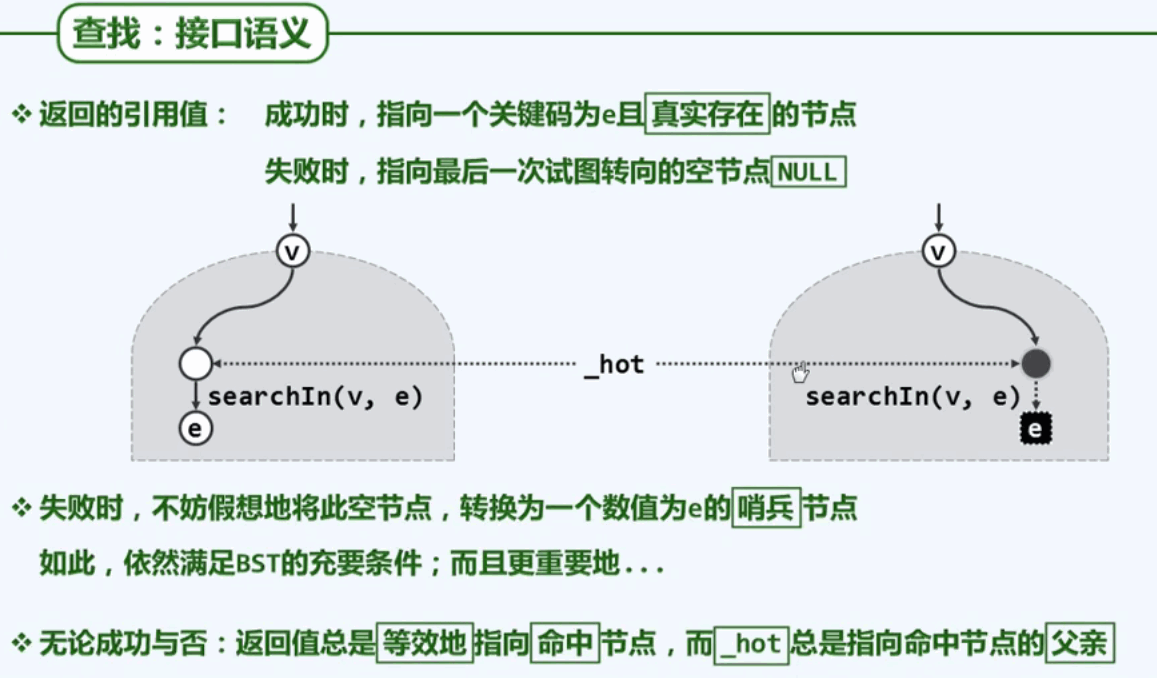
BST的查找算法:

1.对根节点进行一次比较,在有序向量中,对应于基于某个轴点进行比较,摒弃掉树的左子树,也是摒弃掉向量的左侧向量。、
2.每一次都会摒弃掉一颗子树或者一个子向量。
3.如此往复,到最后收缩为只有一个元素。
减而治之策略:
 实现代码:时间复杂度不会超过树的高度。
实现代码:时间复杂度不会超过树的高度。

BST之插入: 先查找再插入一个新的节点
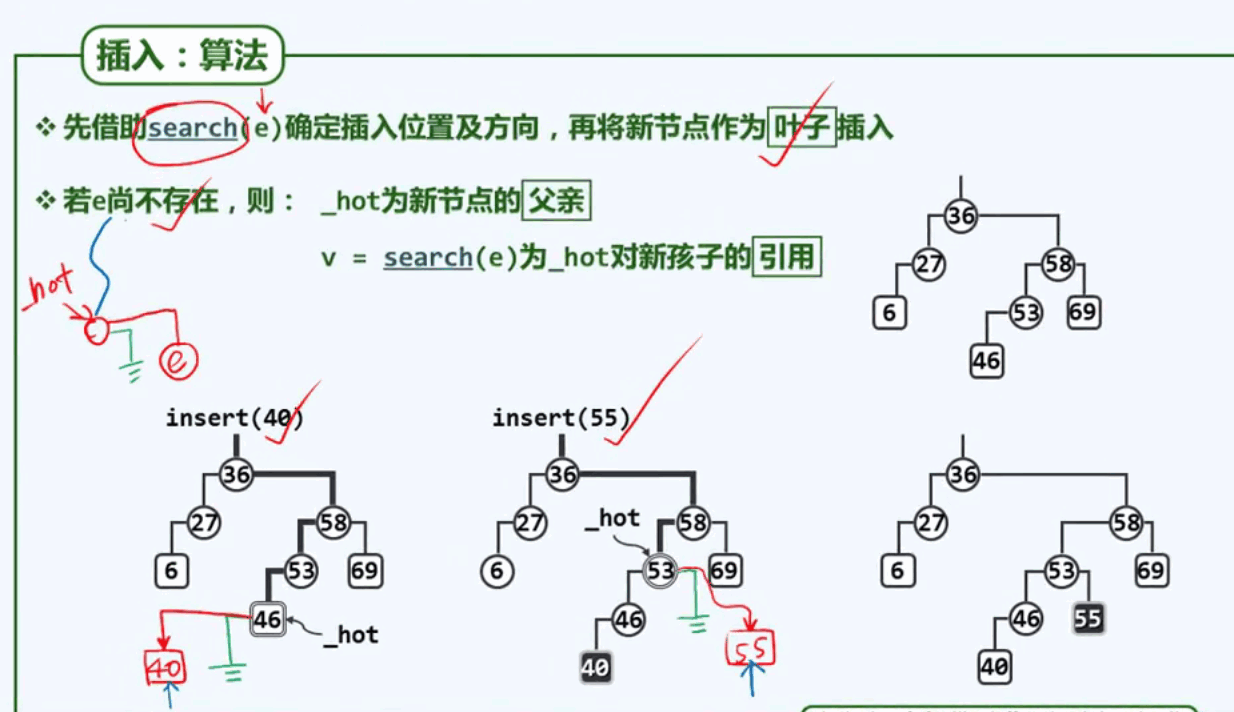
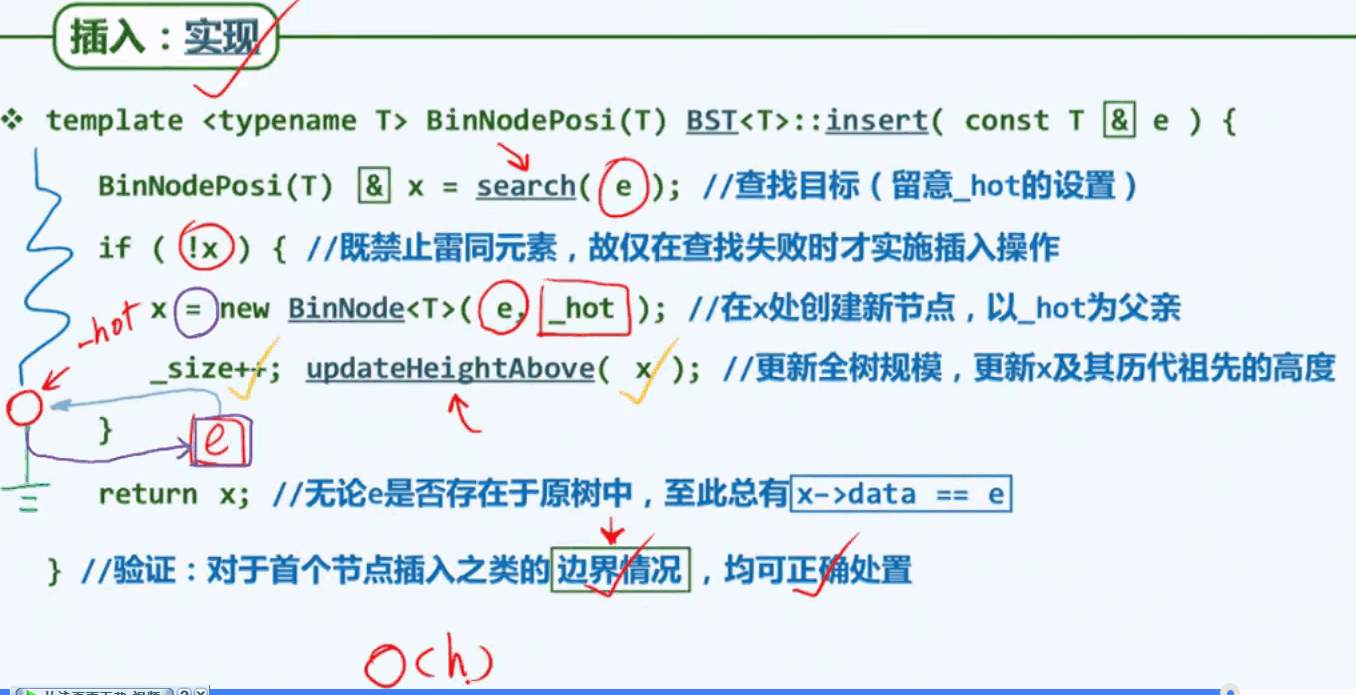
BST删除操作:
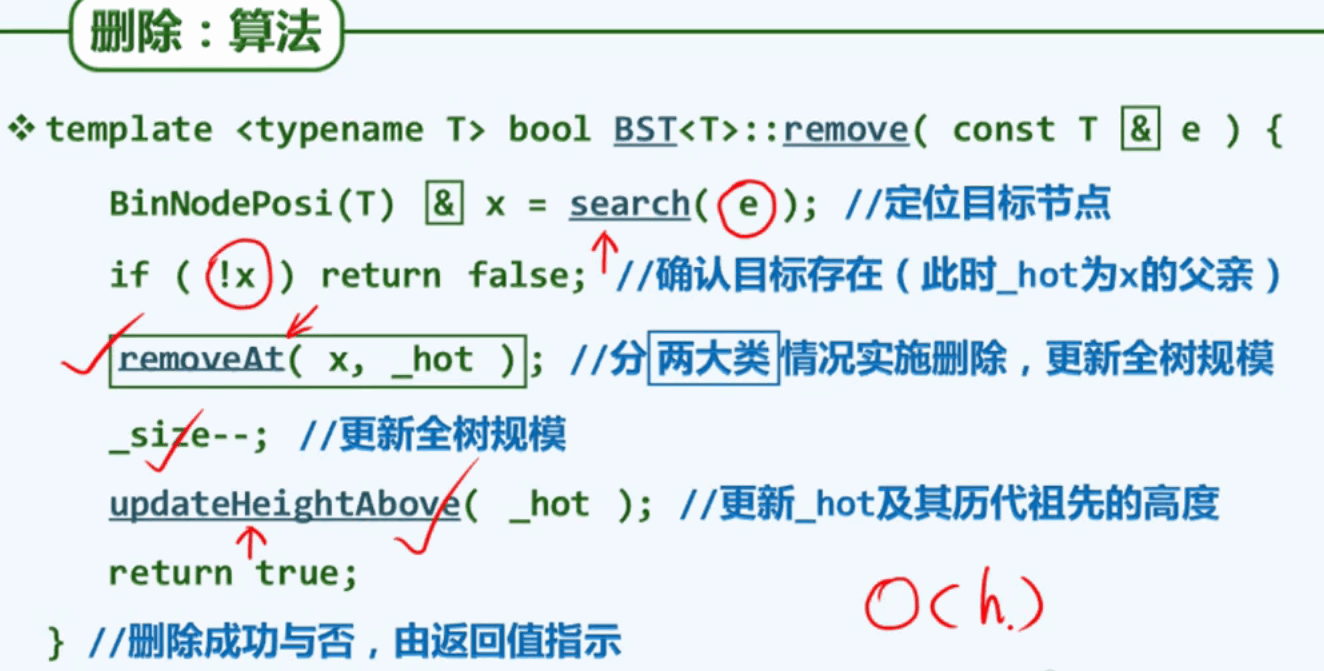
删除情况一:若*x(69)的某一子树为空,则可将其替换为另一颗子树(64)
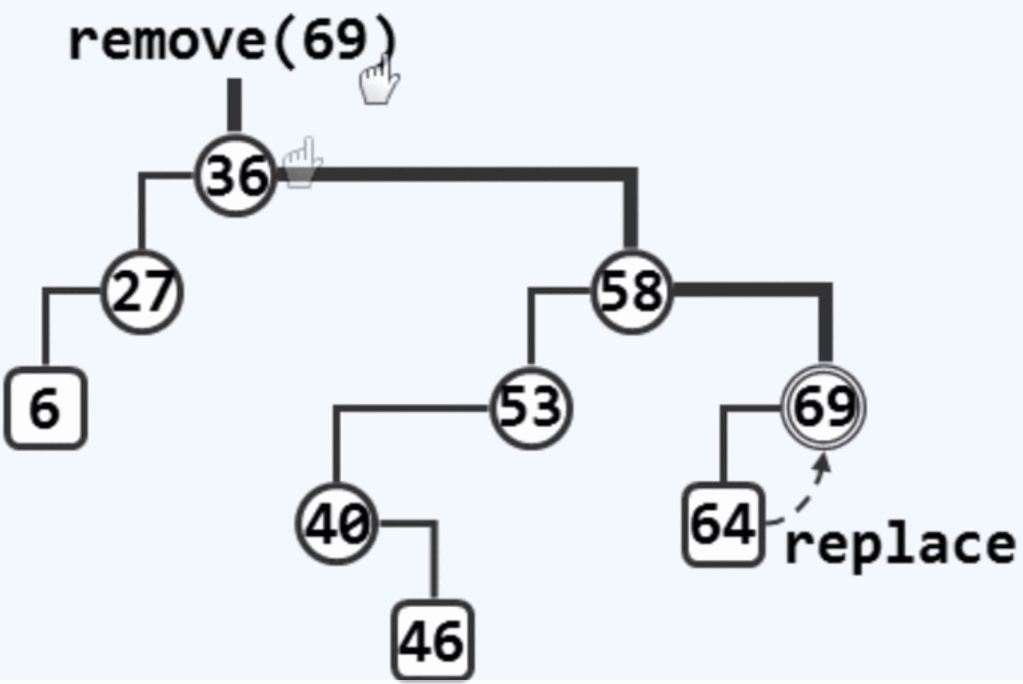

情况二:
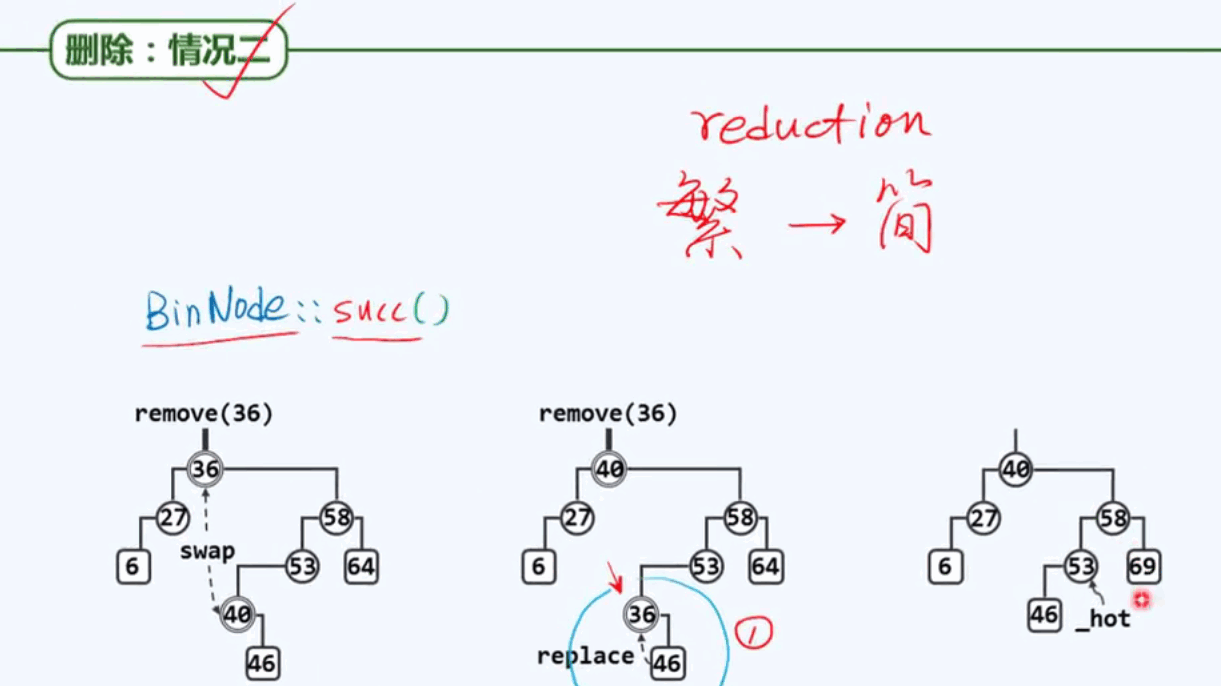
情况二代码:
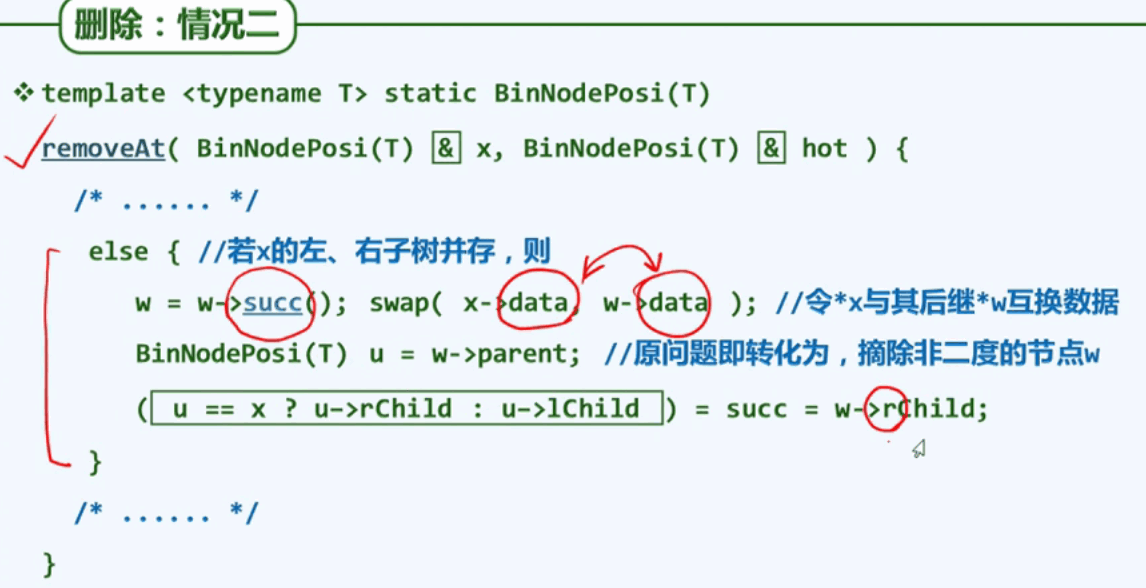
讨论下删除的复杂度:
复杂度不会超过全树的高度O(h),我们无法控制最坏情况下的复杂度,即树的高度h,当树退化成一条单链时(在数据结构上即BST退化成list),其复杂度高达O(n).

随机生成和随机组成:随机组成的高度是根号下n。更可信

二、降低树的高度,来减小复杂度,当兄弟子树的高度越接近平衡,全树叶将倾向于更低。完全二叉树和满二叉树多么完美啊,但是实际应用中不具有意义啊,比如对它们进行删除或插入时,也会失去完美的平衡,哎,悲伤。
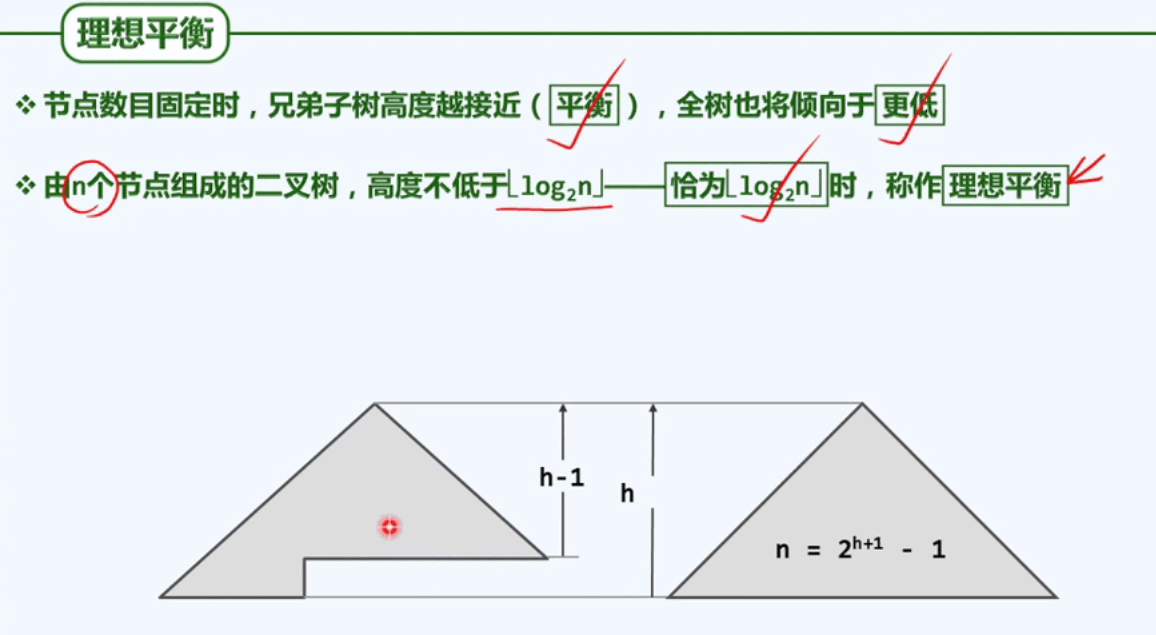
所以我们要适当放松平衡标准,适度平衡的BST,称作平衡二叉搜索树(Balanced Binary Search Tree).

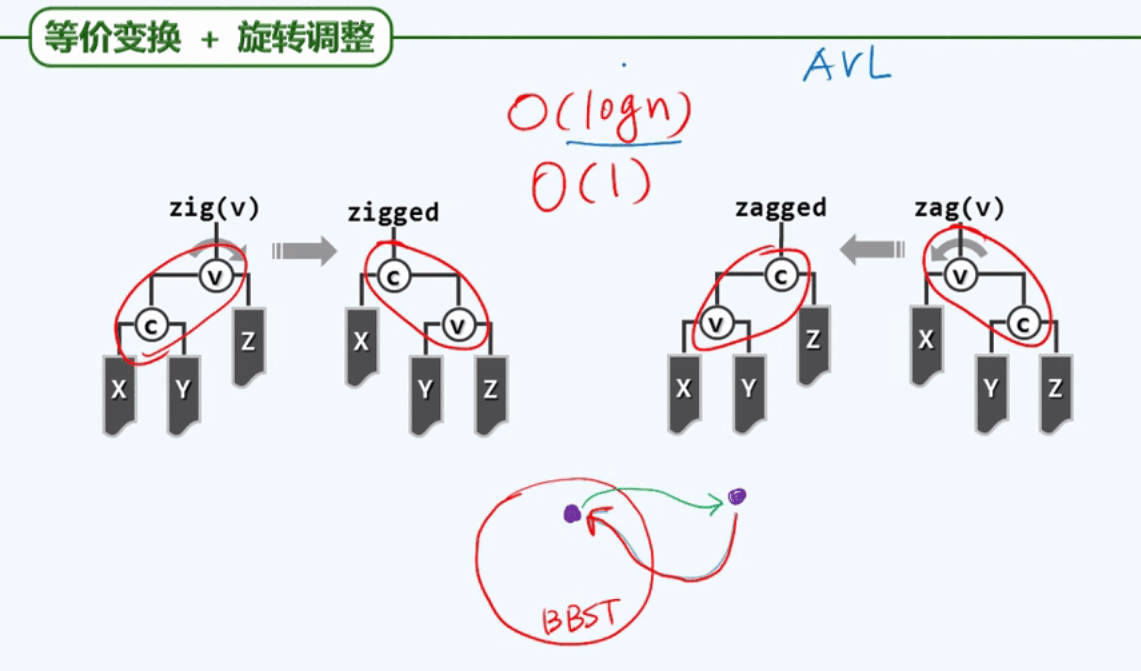
BBST是BST的一个子集,如果在进行某次删除或插入操作以后,BBST跑出了这个子集,变成了一颗BST,那么我们应该怎样把它重新拉回到BBST里呢? 答案是等价变换
中序遍历的歧义性:两颗中序遍历相同的BST,其拓扑结构可能是不同的。
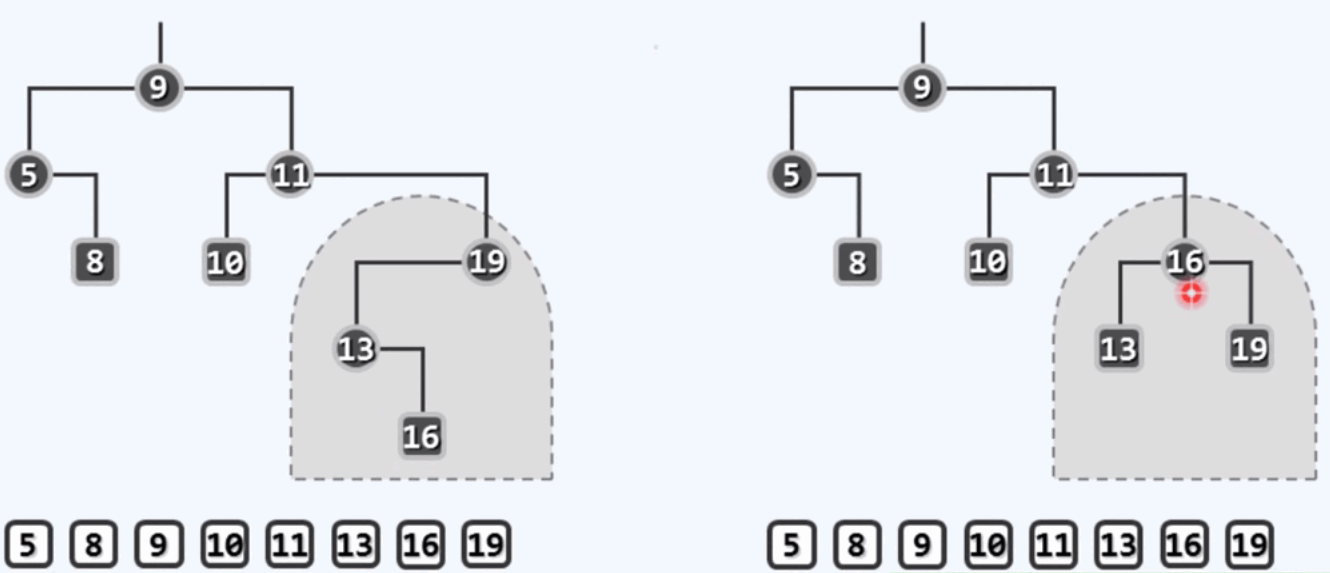

累积需要执行的操作次数不能过多,至多不能超过O(logn),变换应该发生在局部。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号