二叉树的遍历
善于利用之前的轮子:将半线性的二叉树转换成线性结构
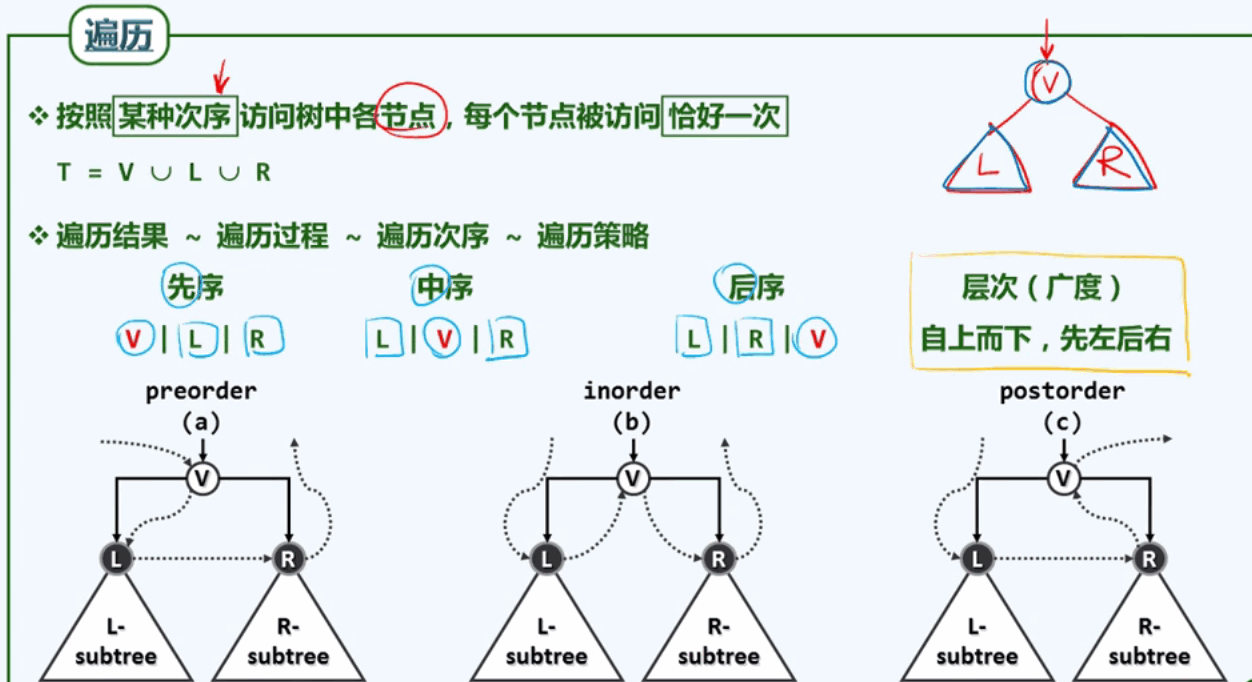
一、先序遍历
递归格式:
递归栈中的每一帧都是具有通用格式的,但显然当递归到深处时,帧的格式应该足够小。
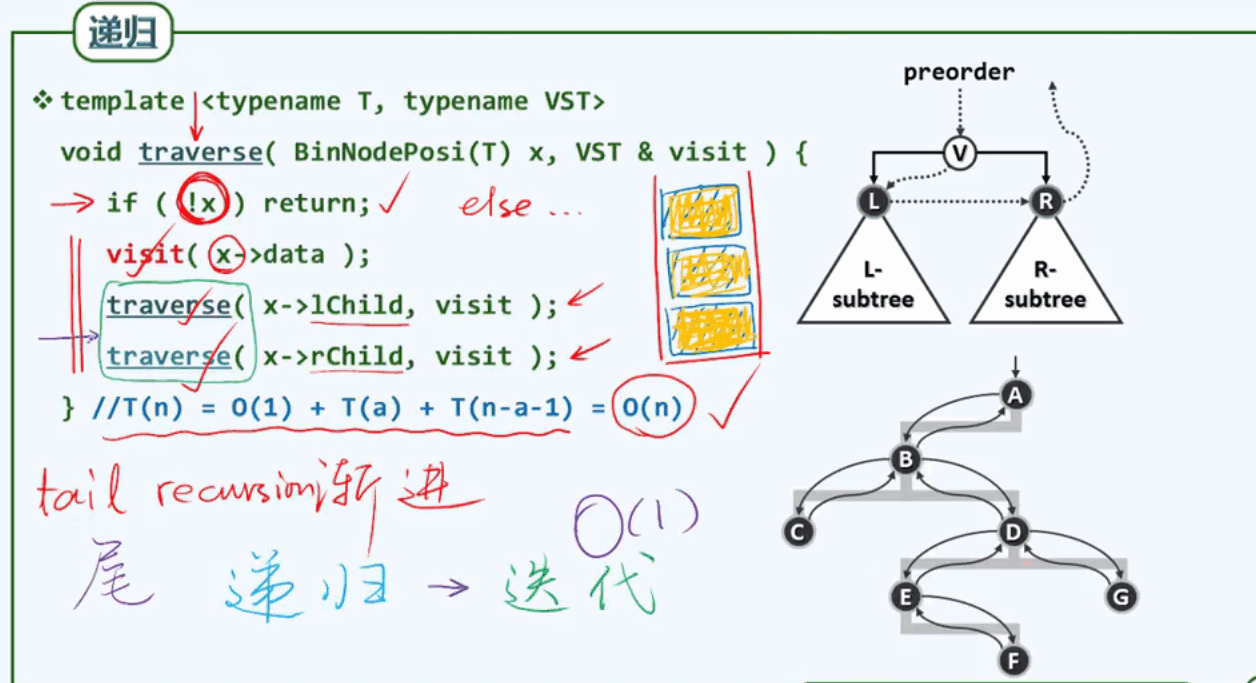
将递归格式转换为栈格式:
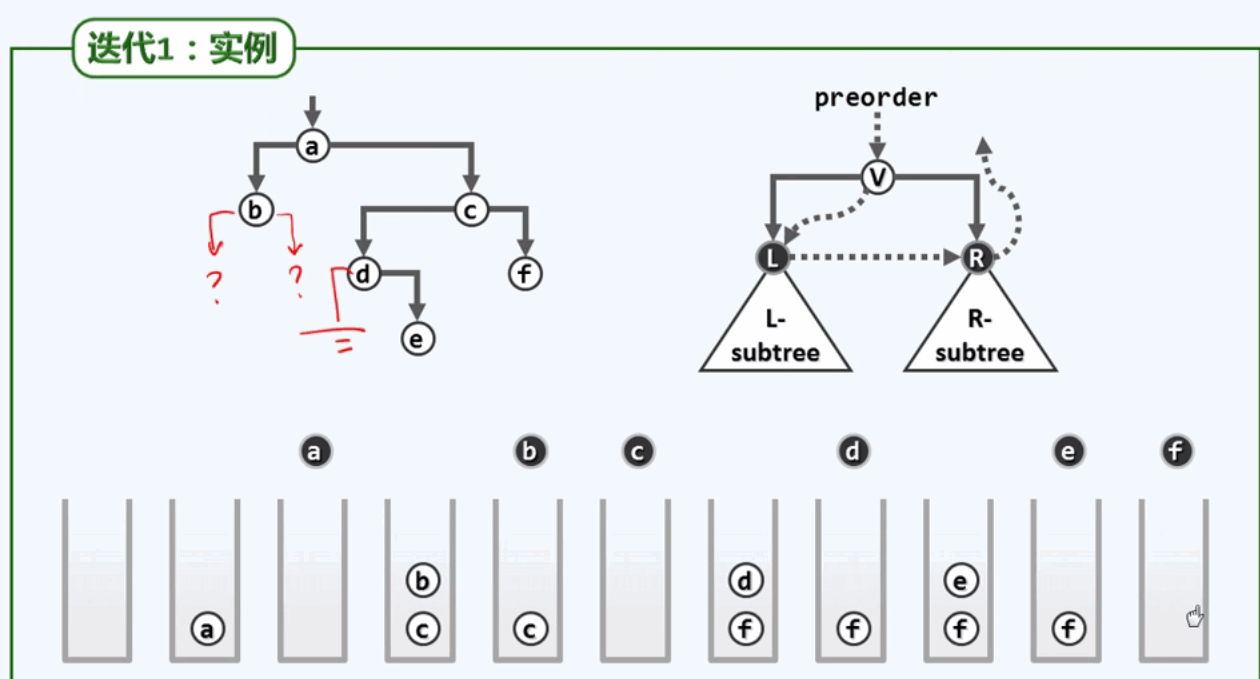
迭代的思路如下所示: 沿着左侧链(总是沿着左侧孩子分支不断下行的一条链)不断展开
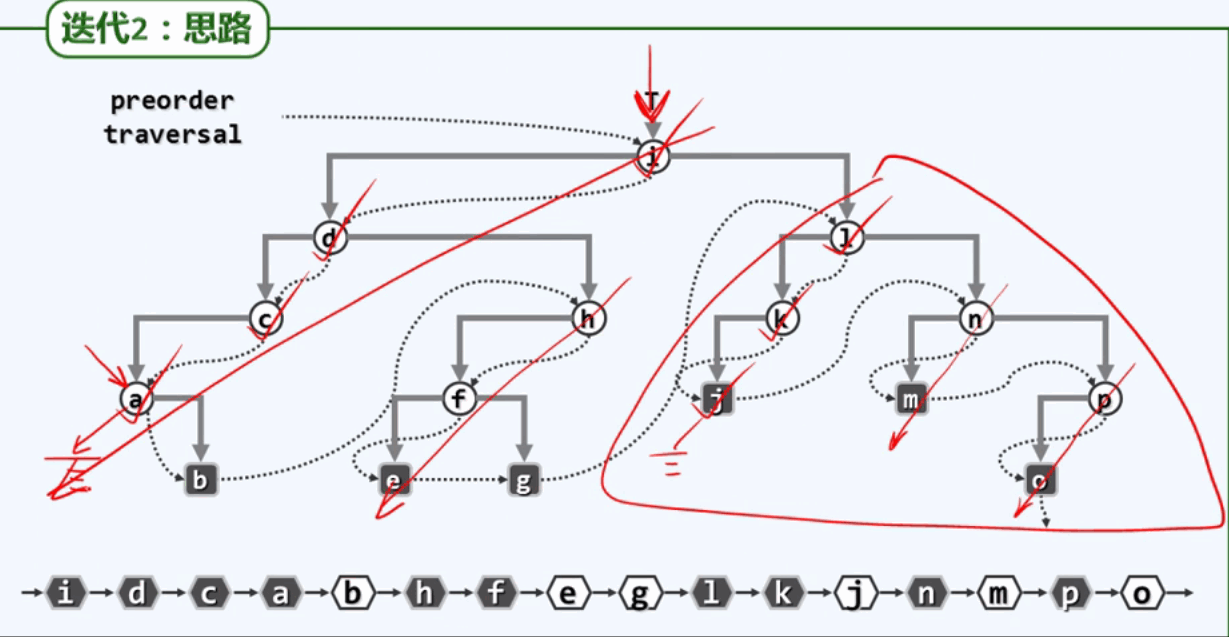
先序遍历:顶而下的依次访问左侧链上的节点,然后再自下而上的依次遍历各个层次上的每一颗右子树:
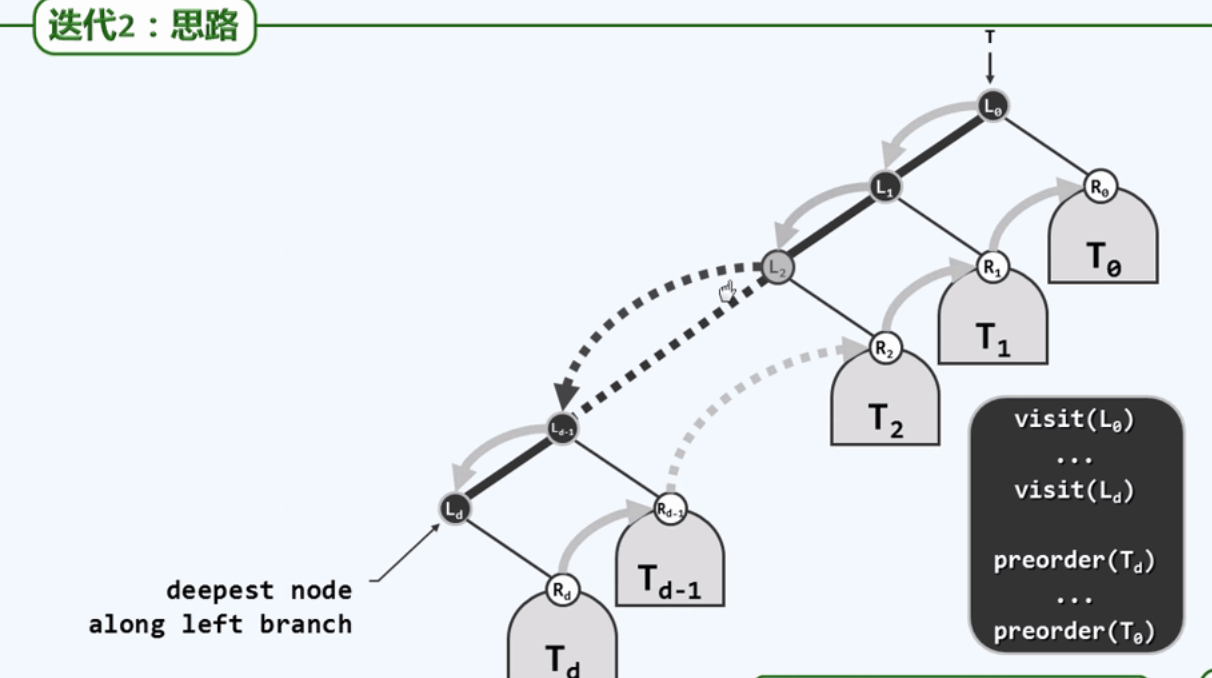
代码实现:
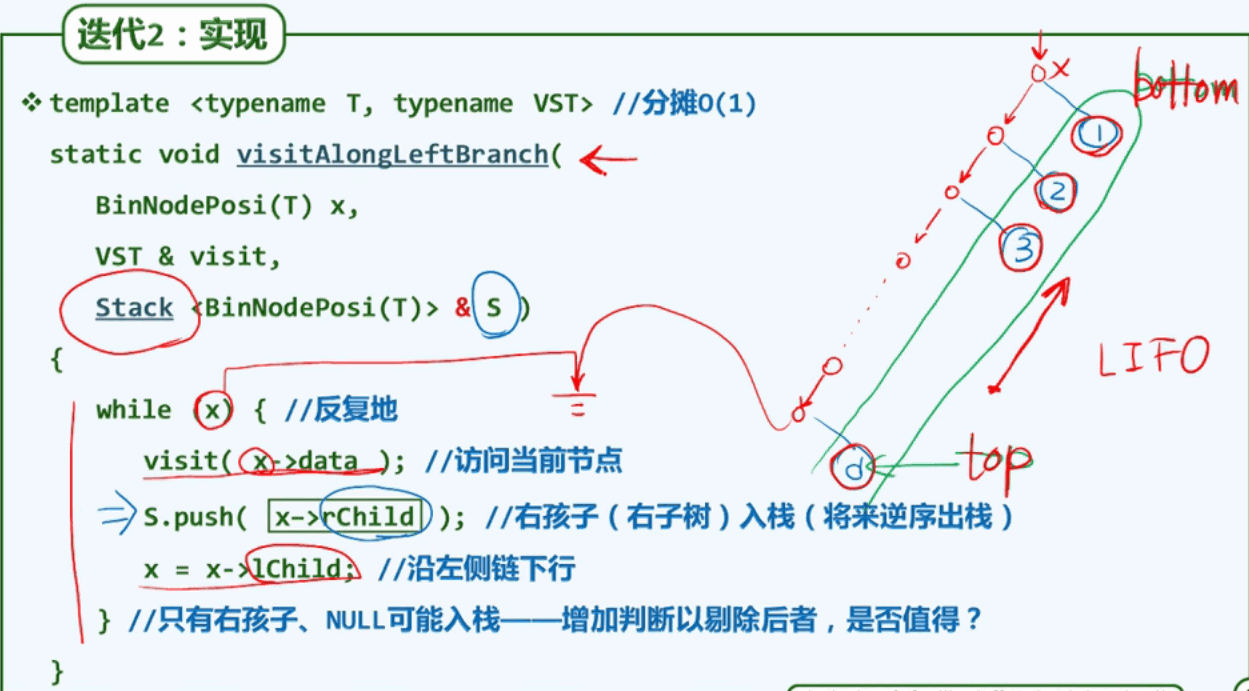
主算法:

实例:
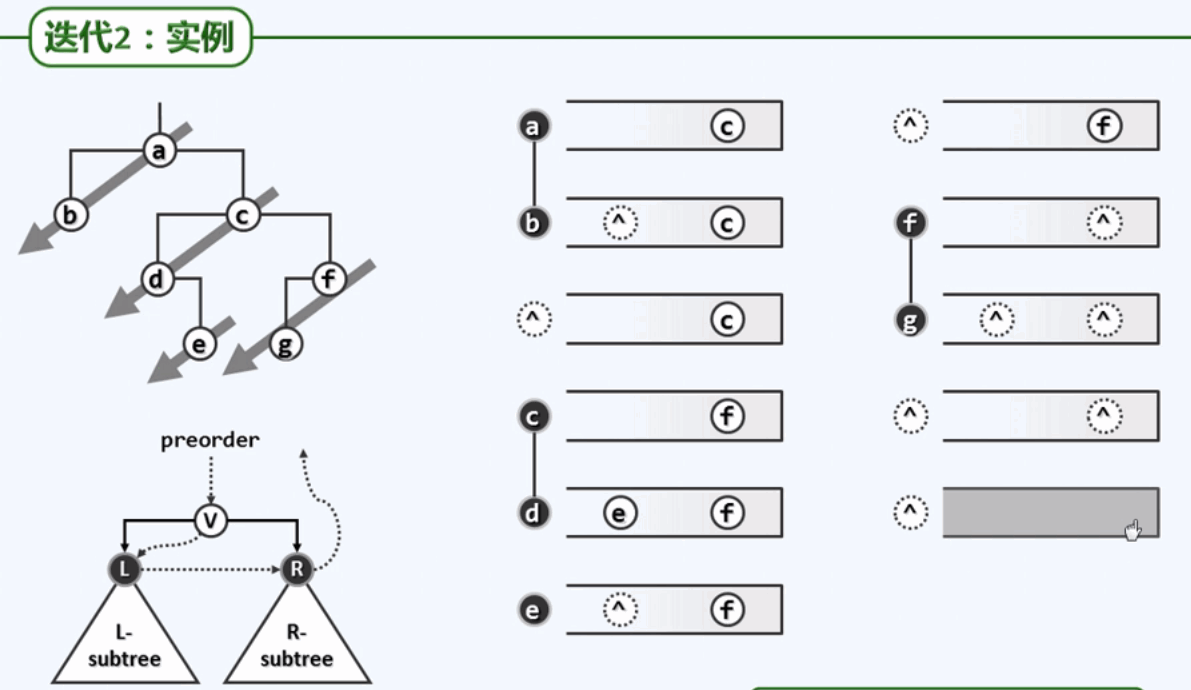
二、中序遍历
先访问左侧子树,再访问根节点,再访问右侧子树。中序遍历要比左序遍历略难,因为在中序遍历中对右子树的访问还是尾递归调用,但是对左子树的调用不是尾递归调用。
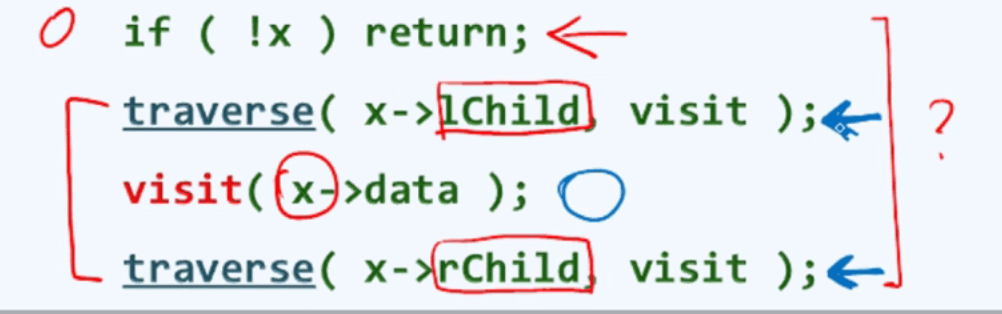
观察规律:
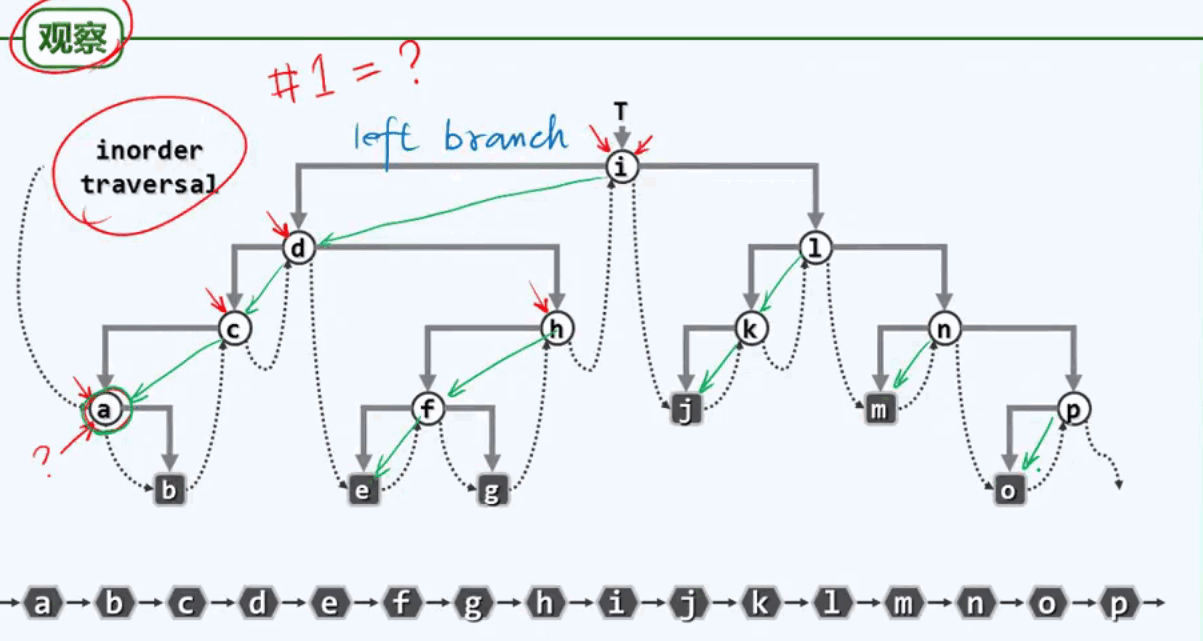
节点访问次序:整个左侧链有多长,就有多少个阶段,访问左侧链节点,遍历右子树,不断重复这个过程。从根出发沿左分支下行,直到最深的节点——它就是全局首先被访问者。(采用某种后进先出的结构)

代码实现:

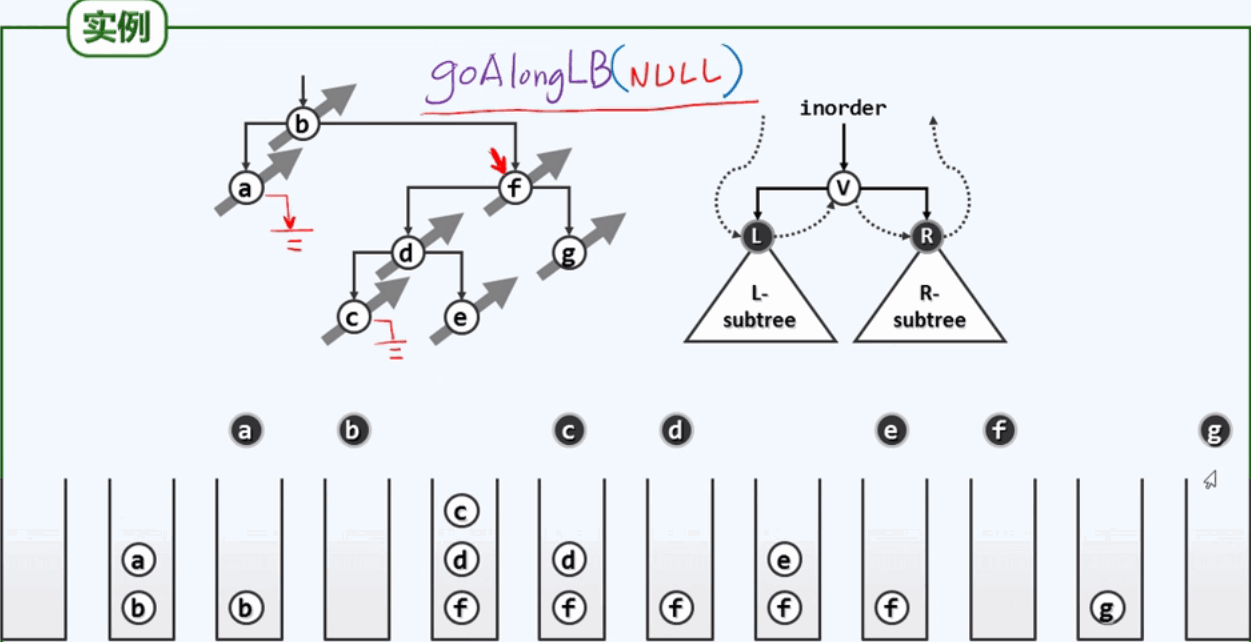
实例:
- 先引入一个栈,初始为空。算法的入口在这棵树的树根,节点b并不会被立即访问,而是沿着左侧链不断下行直到末端节点a,从第一个遇到的b到最后遇到的a都将被推入到栈中
- 先让a出栈,访问a,然后将控制权交给a的右孩子,但是右孩子并不存在,但是也会调用goAlongLeftBranch,但是只是过门,并不会访问。此后b出栈,访问b,然后将控制权转让给b的右孩子。
- 依次重复。
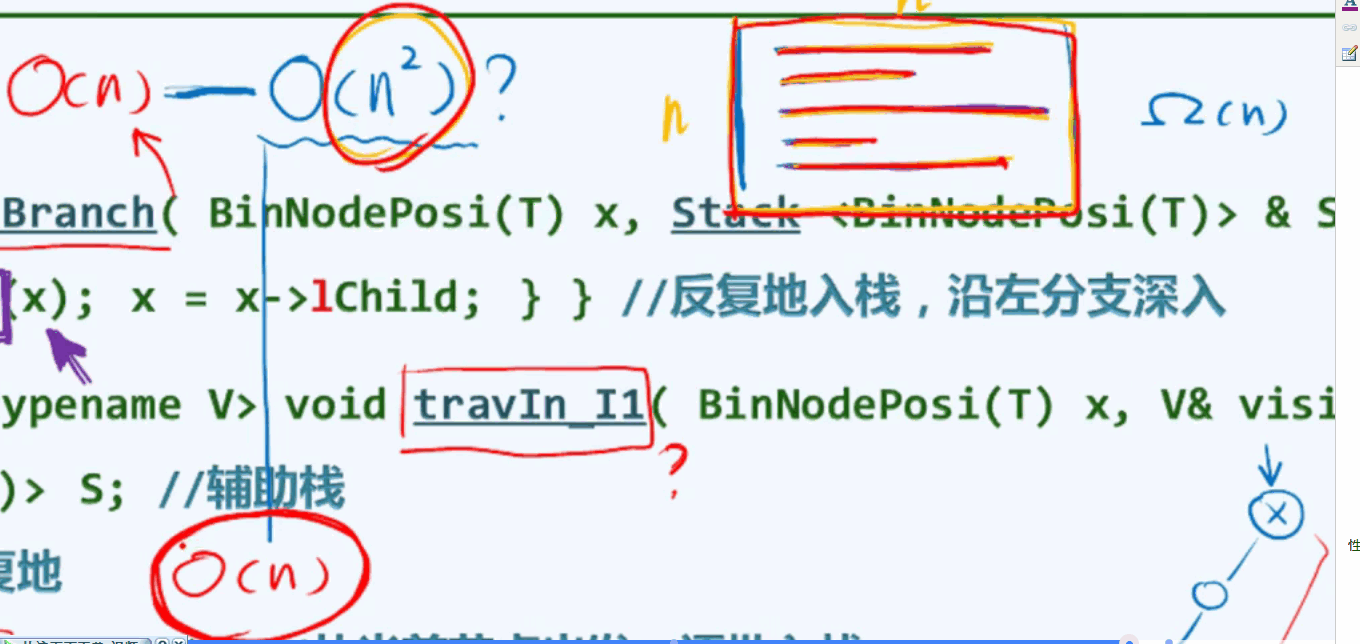
性能分析:
迭代版本的运行时间仍然是O(n),虽然迭代版本的运行时间也是O(n),但是从常系数的意义来讲,其远胜于递归版本。分摊分析法
三、后序遍历
后序遍历是先访问左侧子树,再再访问根节点。
代码如下:

图示如下:
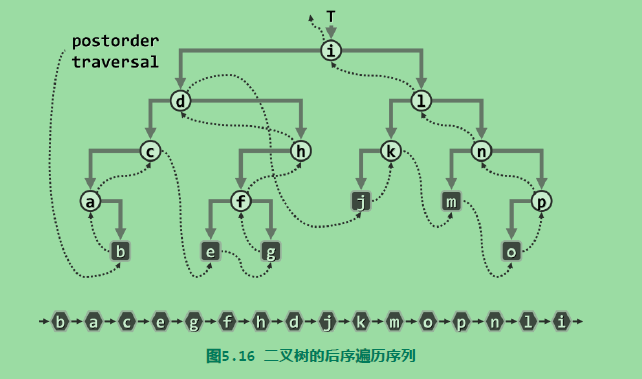
先创建一个空的栈,算法入口是根节点,然后



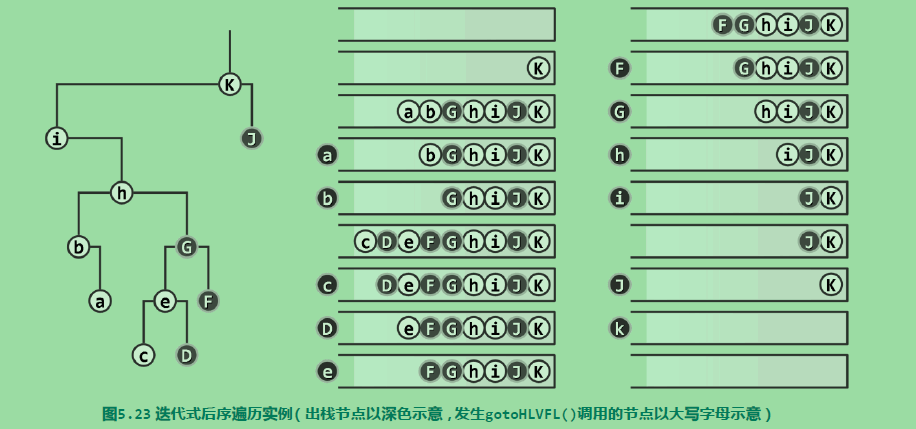
三、层次遍历
从高到低、从左到右。严格按照深度次序来遍历访问。无论先序、中序、后序都可能出现子节点先于父节点访问,而在层次遍历中,严格要求按深度从上到下访问,所以使用队列这种数据结构。
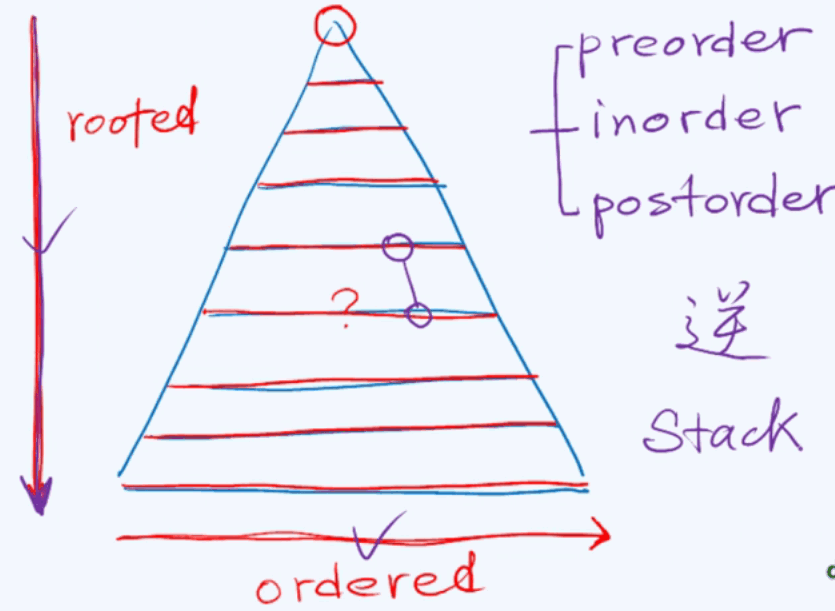
借助队列来实现层次遍历:

二叉树重构:
只需要中序遍历序列一次再加上先序或后序遍历一次,就可以重构整个二叉树的拓扑结构。

