二叉树的实现
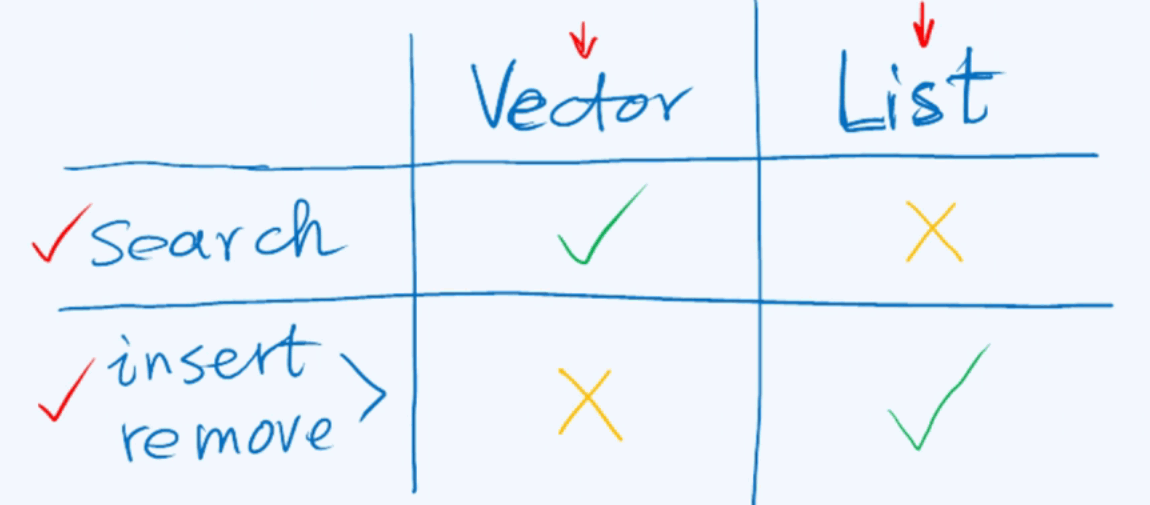
一、vector和list的不足:无法兼顾静态操作和动态操作的性能
二、半线性结构:树 层次关系的表示
- RPN表达式: 1 2 + 3 +

- 域名系统 、大学系统
rooted tree (有根树),子树(subtree)
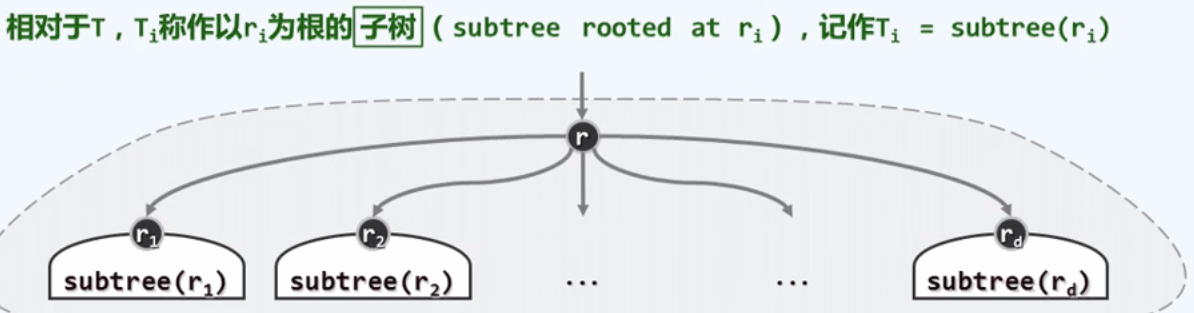
ri称为r的孩子(child),ri之间互称为兄弟(sibling)。r为其父亲(parent) d = degree(r)为r的度(degree).
可归纳如下性质:一棵树的总体规模可以度量为它的顶点数(n)加上边数(e)。
e = degree(r) = n -1
ordered tree (有序树) :给树的各个孩子进行编号。
三、通路和环路
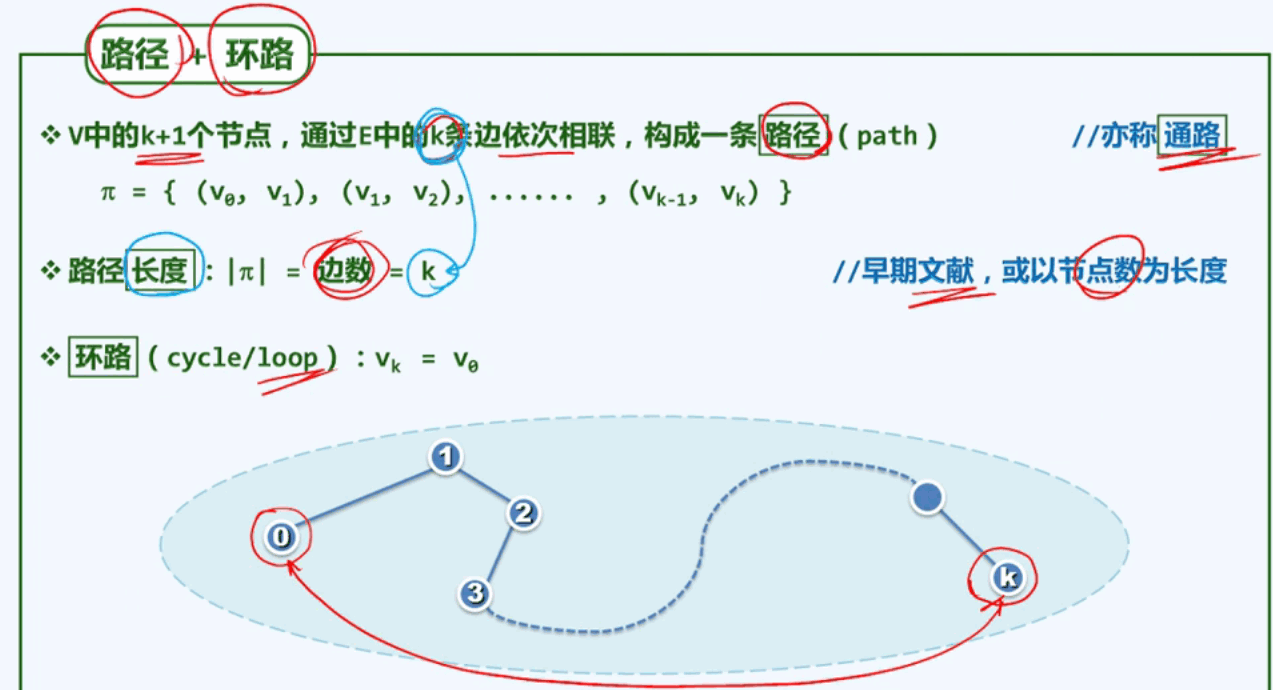

树是一种连通无环图,任一节点v与根节点之间存在唯一路径:path(v,r) = path(v);
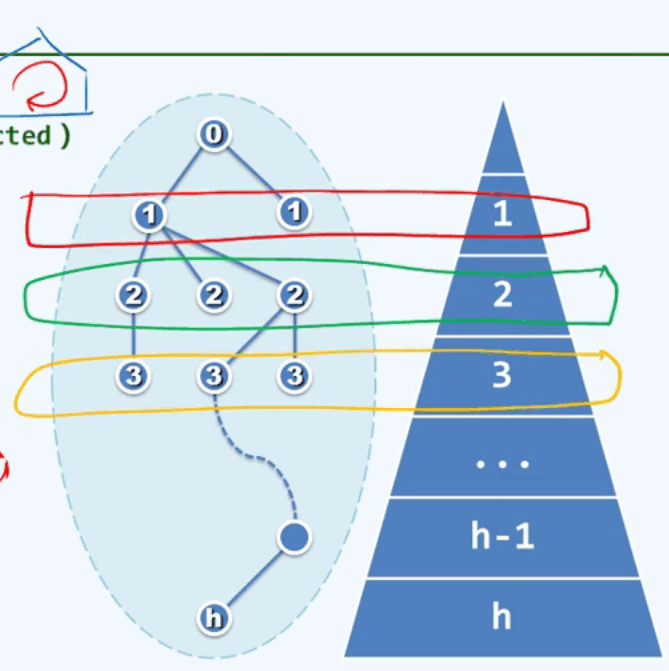
四、深度和层次
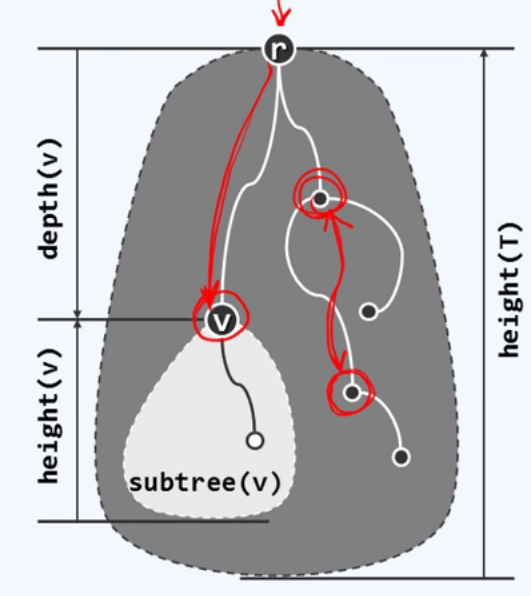
depth(v) =|path(v)| : v所对应的的路径长度path(v)称为节点v在树中的深度。
路径、节点和子树可以互相指代。
path(v)上的节点称为v的祖先(ancestor),v是他们的后代,除自身外,是真(proper)祖先/后代。
半线性结构:在任一深度,v的祖先若存在,则必然唯一,v的后代若存在,则未必唯一。将v的祖先看做前驱,后代看做后继,则前驱必然唯一,后继不唯一。
根节点是所有节点的公共祖先,所对应路径的长度为0,所以深度也为0. 没有后代的节点称为叶子(leaf)。所有叶子深度的最大者,称为树的高度。子树的高度就是根节点的高度。
空树的高度设为-1(现在还不容易理解)。
depth(v) +height(v) <= height(T); 父亲的高度要大于儿子节点的高度。
五、树的接口:

父节点:

孩子节点:
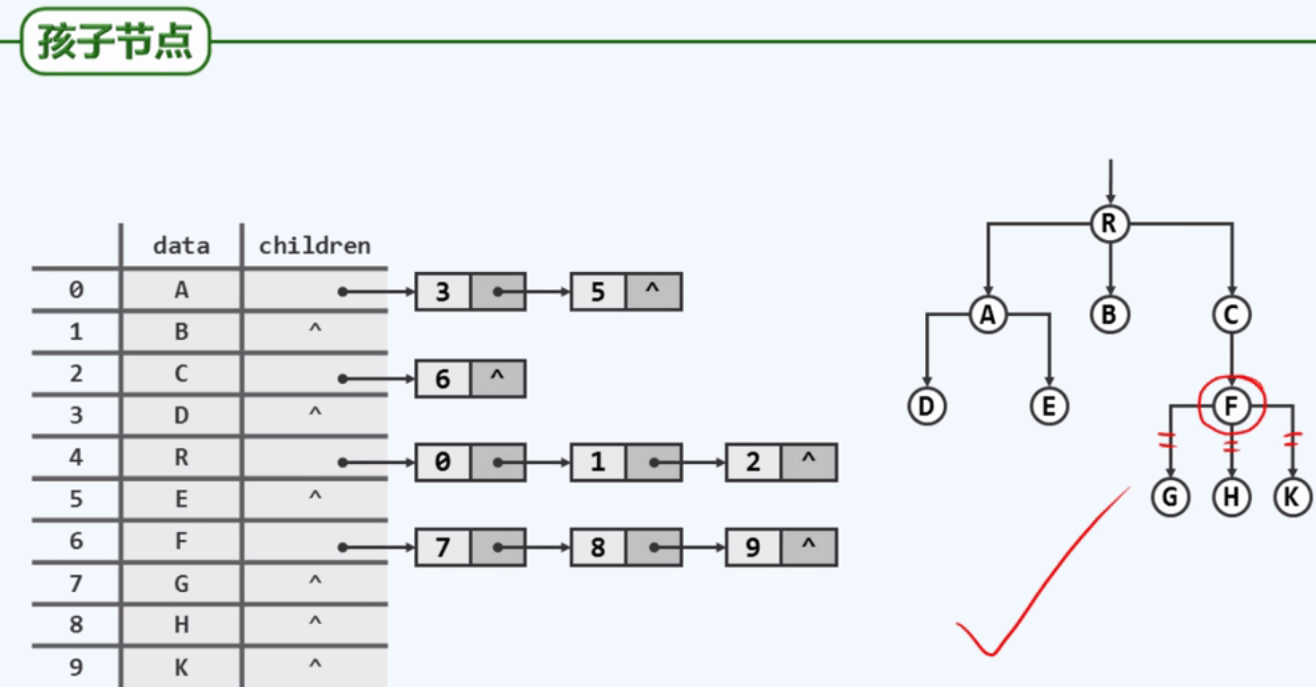
父亲和孩子:

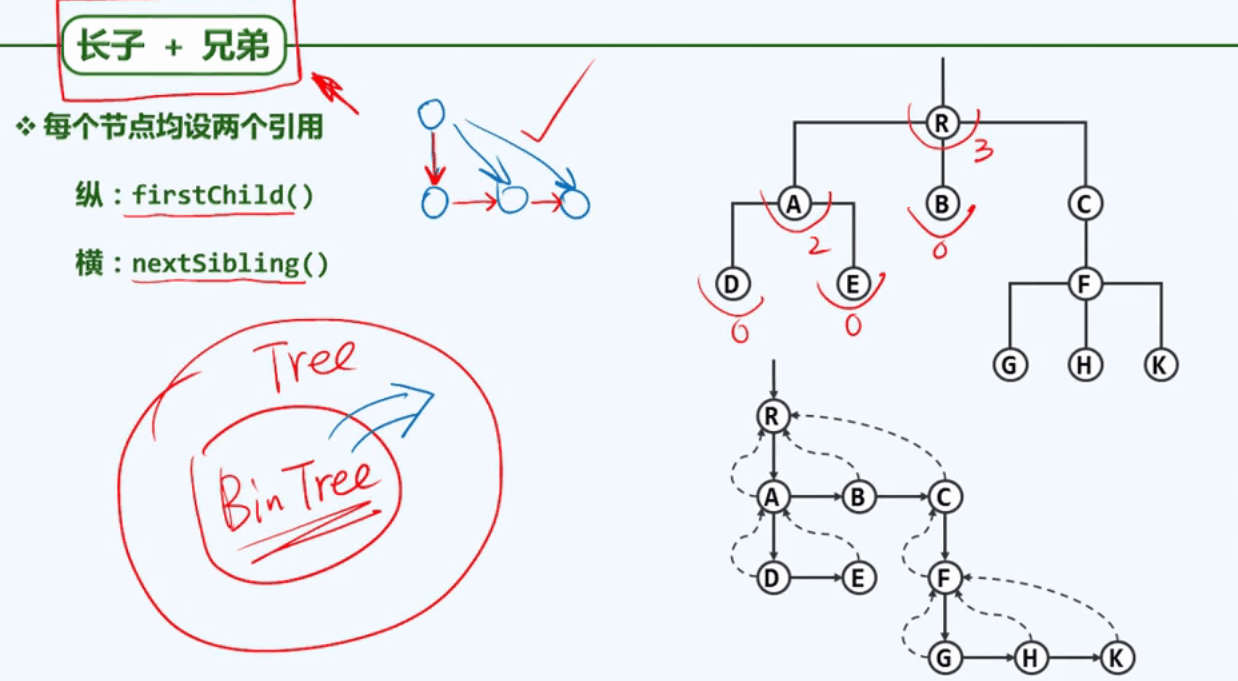
长子+兄弟法:
六、二叉树(binTree)
节点度数不超过2的树,称作二叉树(binary tree)。


满二叉树
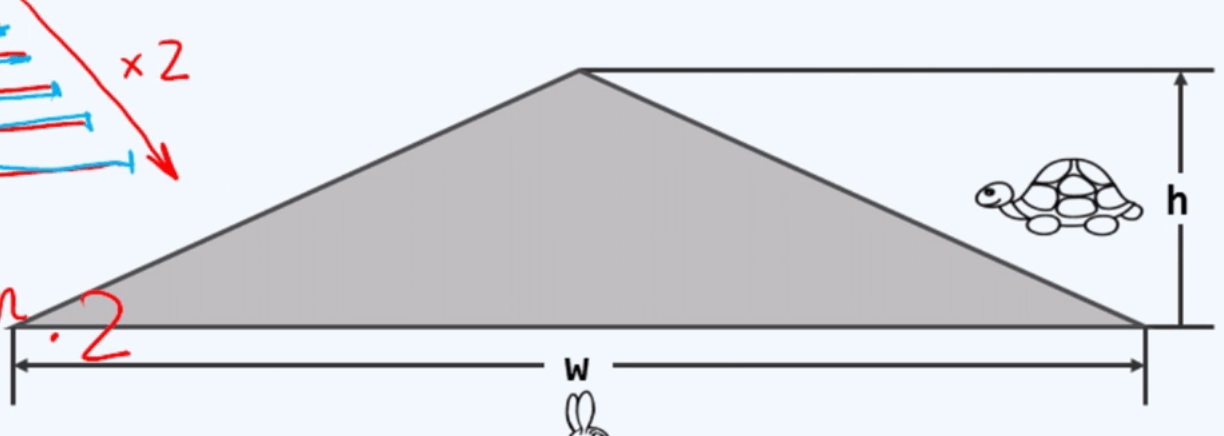
宽度涨的很快,高度很慢。
6.1 真二叉树
每个节点的度都是偶数(2或者0)。 节点有几个分叉,树的度就是几。
6.2 多叉树
二叉树是多叉树的特例,但在有根且有序时,二叉树可以表示多叉树
多叉树通过“长子兄弟法”可以表示为二叉树:(所以只要仔细研究二叉树就可以了)

七、二叉树实现
二叉树节点(BinNode):每个节点通过引用指向其他节点。
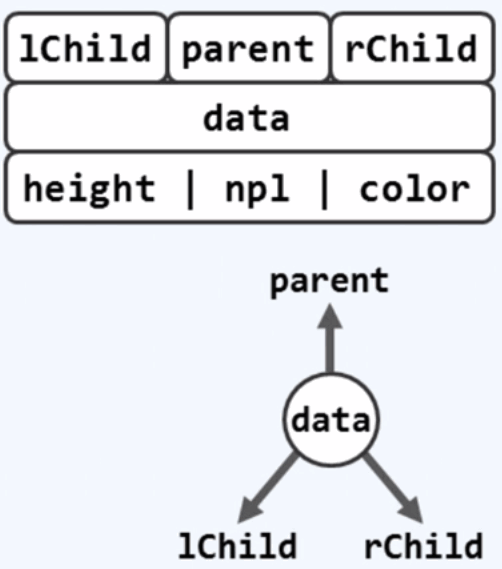

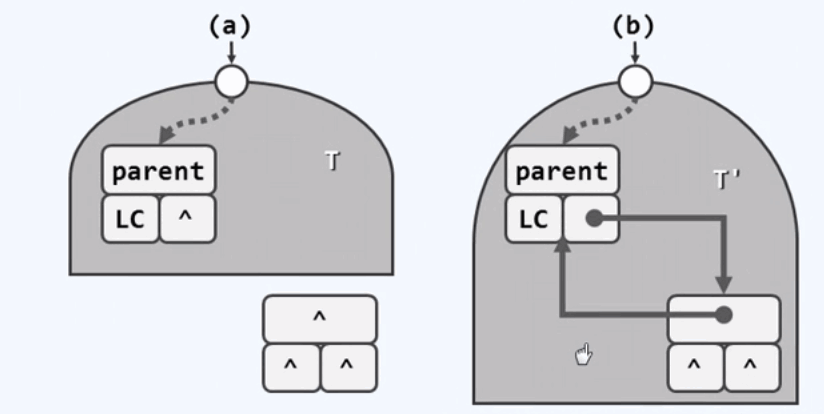
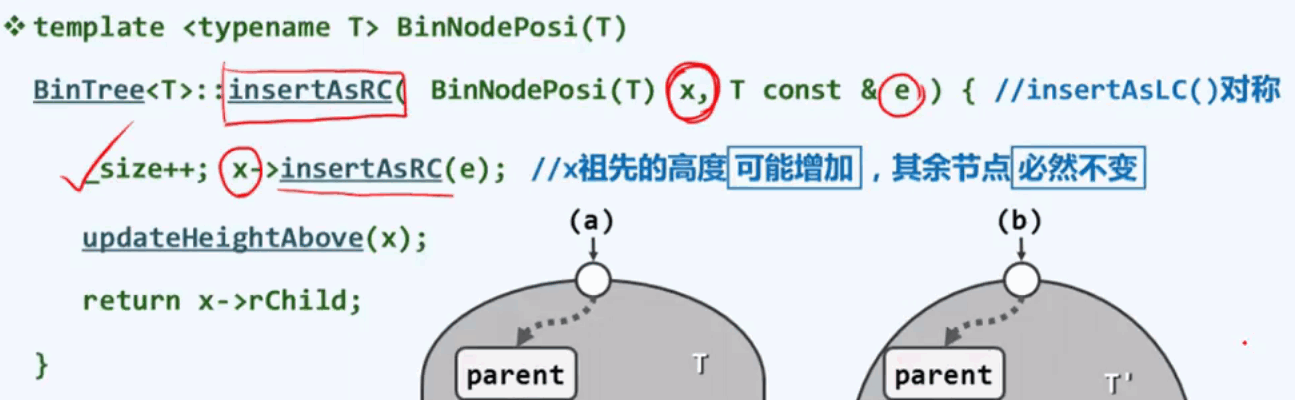
7.1 插入孩子节点:O(1)
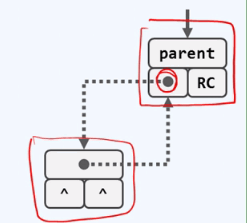

7.2 树的规模:O(n)线性时间

BinTree模板类:
二叉树高度更新:空树h = -1 ,单个节点树h = 0.
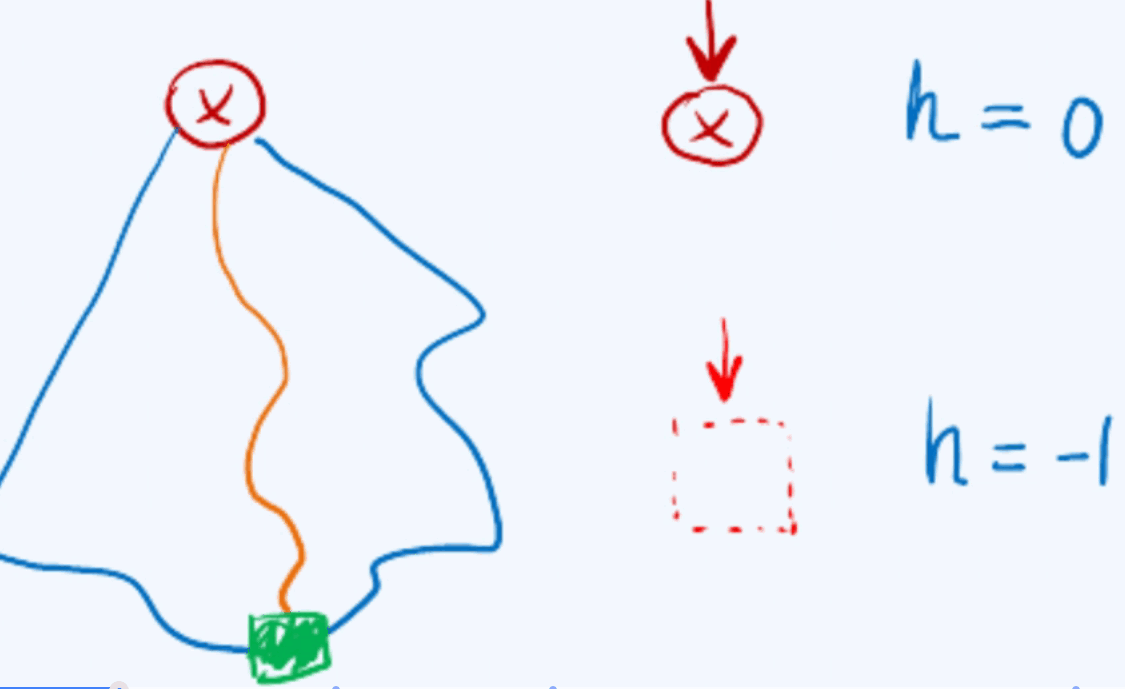
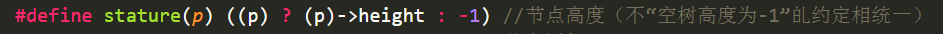
高度更新:

更新节点v及其历代祖先的高度:
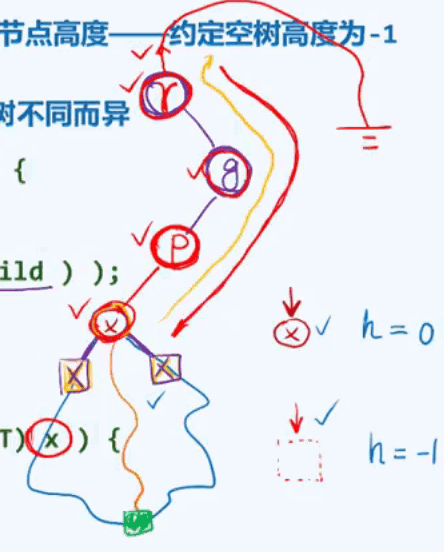

节点插入算法:
将新的节点插入已有树的右孩子:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号