【二叉树】红黑树入门与进阶（算法4）

红黑树

（全称：红黑二叉查找树）

储备知识：你应该有二叉树、二叉查找树（BST）、2-3树的预备知识来学习本节。

 

背后思想：将一个标准二叉查找树和一些额外的信息来表示2-3查找树

 

 

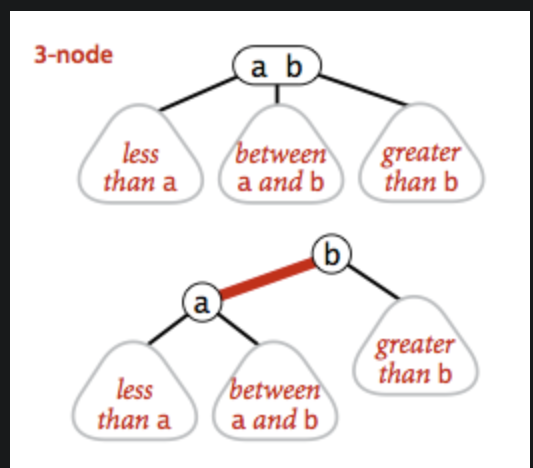
 我们看这张图，图中上部分是一个3节点 下面是一个有红、黑两种颜色的连接

其中左斜红连接相当于 3节点 。

 

红黑树满足条件：

红链接均为左连接

没有一个节点和两个红链接相连

该树完美黑色平衡的，即任意空连接到根节点路径上的黑链接数量相等

 

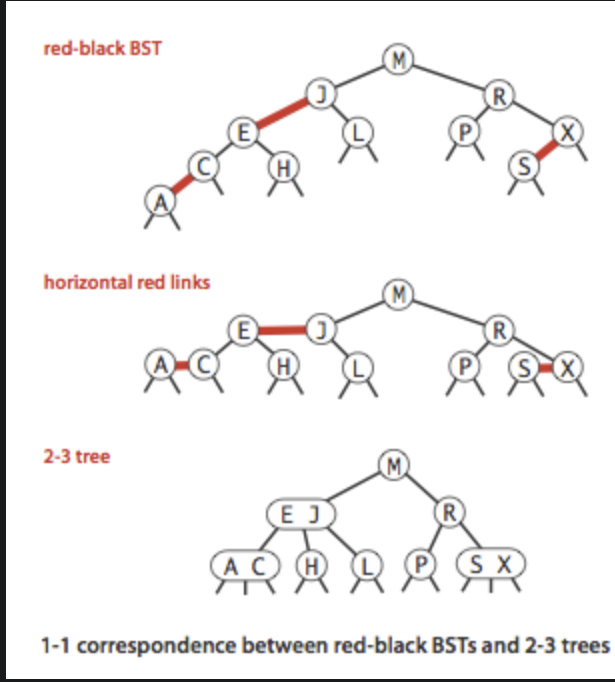
红黑树向2-3树的演变过程：我们看到就是红链接放平，然后将红链接的两个键 ，合并为3节点，就变成一个2-3树

（反着看就是2-3树到红黑树的演变过程）

 

 

 

 

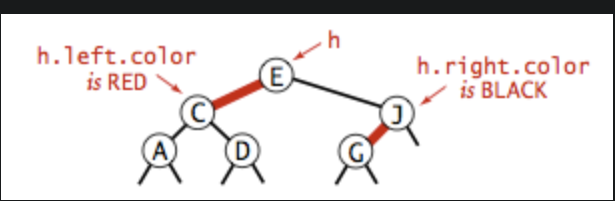
我们规定，由父节点指向当前节点的连接的颜色 保存在Node数据变量color中

例如下图：E黑色、C红色、J黑色、G红色

 

 

 

旋转：

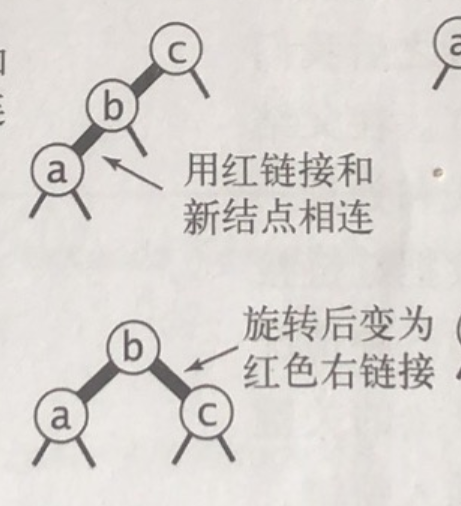
有时候我们会遇到红链接是右连接怎么办？

如下图，进行左旋转，进行左、右引用的变换 以及 color的重赋值

 

 

 

右旋转同理

虽然红黑树的红链接都是左连接，那么右旋转为啥还要有呢？原因是在进行标准化的时候有）

 

 

 

 

 

一、向一个只有一个2节点的树插入节点

（1）直接插入生成一个3节点后，变成红链接

 

 

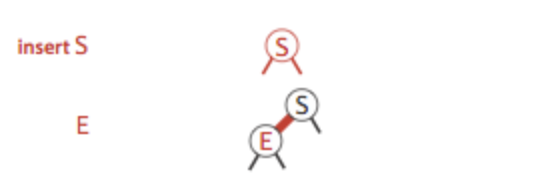
 （2）插入3节点后，生成3节点，但红链接在右侧，需要左旋转进行红黑树的标准化

 

 

 

二、向树底部的2节点插入新键

（1）如果是新节点是父连接的左儿子节点，红链接在左面，不需要更多的操作

（2）如果新节点是父连接的右儿子，则需要一次左旋转，如下图

 

 

 

三、向一个只有一个3节点的树插入 的3种情况

 

 在第二种情况下，新键最小，会出现2条红链接，我们进行如下变换（将2个红链接变为黑，但将父节点的color变成红）

 

 四、向树的底部3节点插入

 

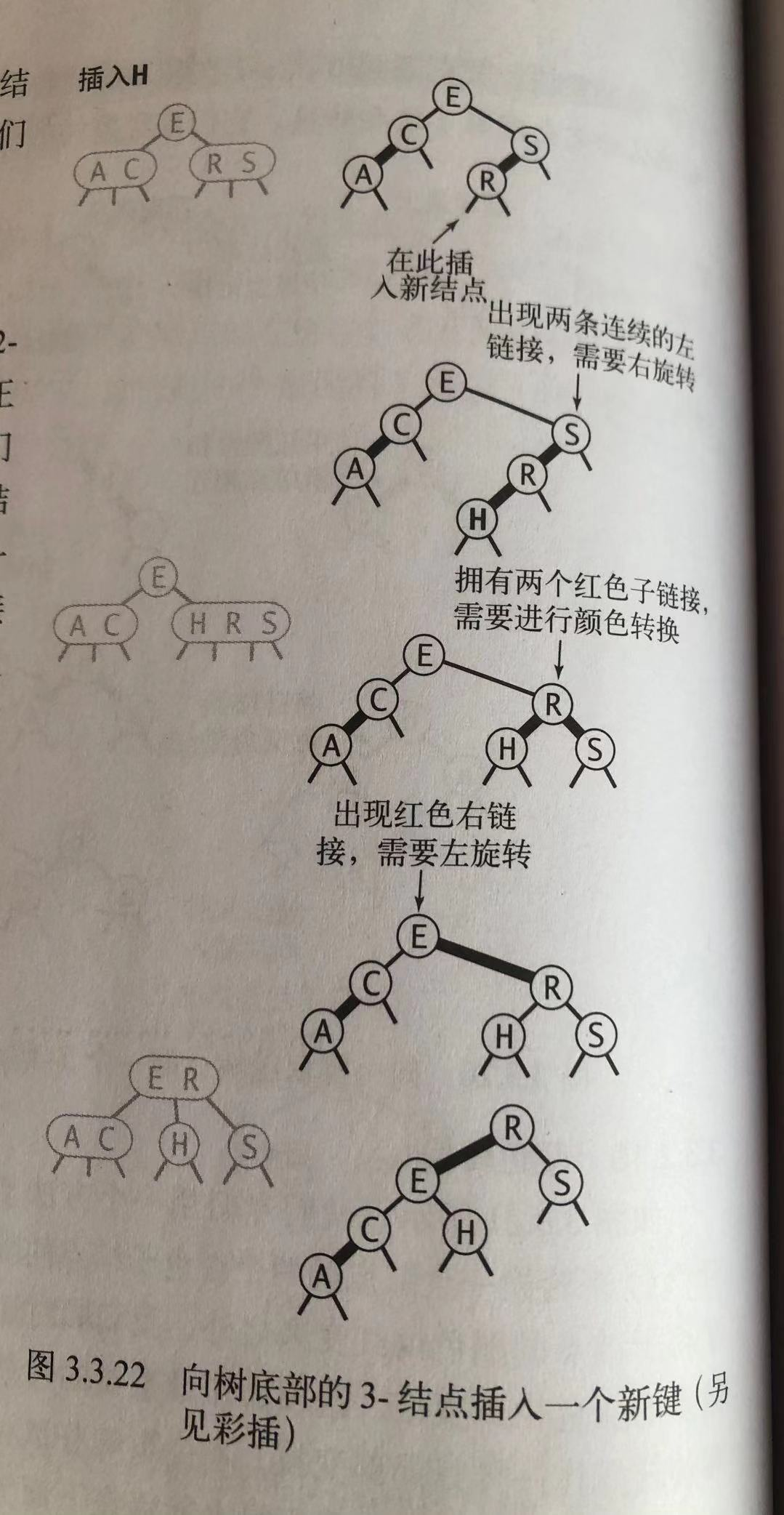
 总结：只要善于使用左旋转、右旋转、颜色变换 3个特性 就能保证红黑树与2-3树的一一对应关系。