《HybridSN: Exploring 3-D–2-DCNN Feature Hierarchy for Hyperspectral Image Classification》论文阅读

《HybridSN: Exploring 3-D–2-DCNN Feature Hierarchy for Hyperspectral Image Classification》论文阅读

一、引言

  • 高光谱图像是立体数据，也有光谱维数，仅凭2D-CNN无法从光谱维度中提取出具有良好鉴别能力的feature maps。一个深度3D-CNN在计算上更加复杂，对于在许多光谱带上具有相似纹理的类来说，单独使用似乎表现得更差。
  • 混合CNN模型克服了之前模型的这些缺点，将3D-CNN和2D-CNN层组合到该模型中，充分利用光谱和空间特征图，以达到最大可能的精度

二、详细内容

2.1 基础知识扫盲

  • 单色光：单一波长（或频率）的光，不能产生色散。

  • 复色光：几种单色光合成的光。

  • 色散系统：复色光分解为单色光而形成光谱的现象。

  • 光谱（光学频谱，spectrum）：复色光经过色散系统（如棱镜、光栅）分光后，被色散开的单色光按波长（或频率）大小而依次排列的图案。

  • 光栅：由大量等宽等间距的平行狭缝构成的光学器件。

  • 高光谱图像（Hyperspectral Image）：在光谱的维度进行了细致的分割，不仅仅是传统的黑，白或者RGB的区别，而是在光谱维度上也有N个通道。例如：我们可以把400nm-1000nm分为300个通道，一次，通过高光谱设备获取的是一个数据立方，不仅有图像的信息，并且在光谱维度上进行展开，结果不仅可以获得图像上每个点的光谱数据，还可以获得任意一个谱段的影像信息。

  • 高光谱图像成像原理：空间中的一维信息通过镜头和狭缝后，不同波长的光按照不同程度的弯散传播，一维图像上的每个点，再通过光栅进行衍射分光，形成一个谱带，照射到探测器上，探测器上的每个像素位置和强度表征光谱和强度。

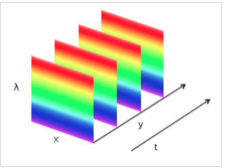
在这里插入图片描述

  • HSI：数字图像模型，反映了人的视觉系统感知彩色的方式，以色调H（Hue）、饱和度S（Saturation）、亮度I（Intensity）三种基本特征量来感知颜色。
    • 色调H（Hue）：与光波的频率有关，它表示人的感官对不同颜色的感受，也可以表示一定范围的颜色；
    • 饱和度S（Saturation）：表示颜色的纯度，纯光谱色是完全饱和的，加入白光会稀释饱和度。饱和度越大，颜色看起来就越鲜艳。
    • 亮度I（Intensity）：对应成像亮度和图像灰度，是颜色的明亮程度。

2.2 实现过程

  • 空间光谱高光谱数据立方体表示为：

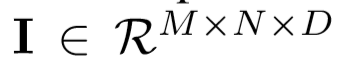
    • I为原始输入，M为宽度，N为高度，D为光谱带数/深度
    • I中的每个HSI像素包含D个光谱测度，形成一个one-hot向量

  • 然而, 高光谱像素 exhibit the mixed land-cover classes（？？）, introducing the high intra-class variability and interclass similarity into I.（个人理解为，引入这两个性质比较难办）因此：

    1. 将主成分分析（PCA）应用于原始HSI数据（I）的光谱波段（将光谱波段从D减少到B，保持相同的空间维数），只减少了光谱波段，保留了对识别物体重要的空间信息。

    2. 下式为处理后的数据立方体，其中X为PCA后的输入，M为宽度，N为高度，B为主成分后的光谱带数。

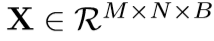
    3. 将HSI数据立方体划分为重叠的三维小块，小块的truth label由中心像素的label决定。

    4. 从X开始，创建以空间位置（α，β）为中心的三维相邻块，覆盖了S×S的窗口或者是空间范围和所有B光谱波段。

    5. 在（α，β）上的三维块覆盖了宽度从α-(S-1)/2到α+(S-1)/2，高度从β-(S-1)/2到β+(S-1)/2和所有的PCA简化立体数据X的B光谱波段。

    6. 在二维卷积中，第j个特征图的i层中(x,y)位置的激活值表示如公式（1）下：

      （其中φ是激活函数,bi, j是第j个特征图的i层的偏差参数,dl−1是第(l−1)层特征图的数量和第i层j个特征图的数量,2γ+ 1是卷积核的宽度，2δ +1 是卷积核的高度，wi,j 为第i层j个特征图权重指数的值）

    image-20200808095629078

  • 在HSI数据模型中，利用三维核在输入层的多个连续频带上生成卷积层的特征图，捕获了光谱信息；在三维卷积中，在第i层第j个特征图中（x,y）的激活值记为Vx,y, Zi,j，如公式（2）所示：

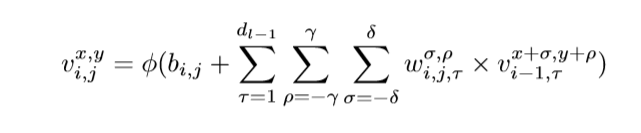
  • 2η + 1 为卷积核沿光谱维数的深度，其他参数不变。

2.3 混合特征学习框架hybrid feature learning framework

网络结构如图所示（三个三维卷积【公式2】，一个二维卷积【公式1】，三个全连接层）：

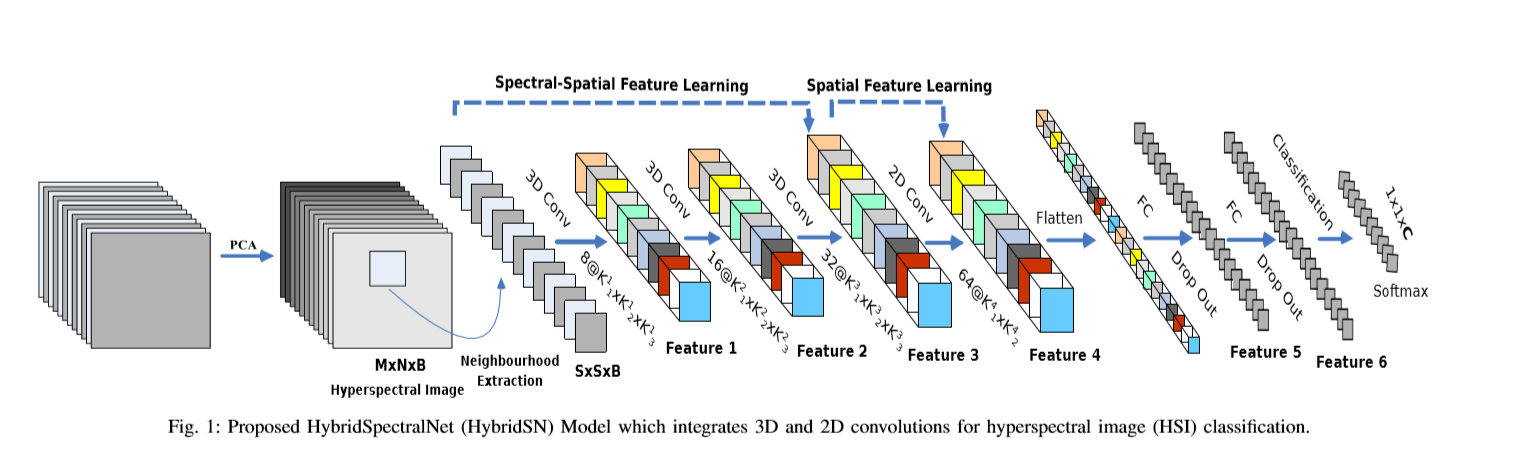
  • 三维卷积中，卷积核的尺寸为8×3×3×7×1、16×3×3×5×8、32×3×3×3×16（16个三维核，3×3×5维）
  • 二维卷积中，卷积核的尺寸为64×3×3×576（576为二维输入特征图的数量）

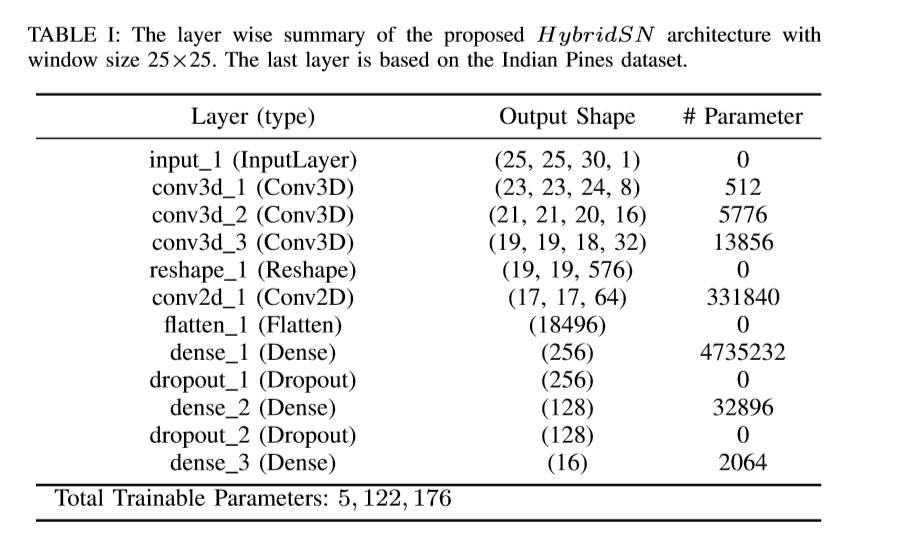
2.4 实验数据集

三种开源高光谱图像数据集，Indian Pines（IP）, University of Pavia（UP） and Salinas Scene（SA）

  • IP图像空间维度为：145×145，波长范围为400-2500nm，共有224个光谱波段
  • UP图像空间维度为：610×340，波长范围430-860nm，共有103个光谱波段
  • SA图像空间维度为：512×217，波长范围360-2500nm，共有224个光谱波段

2.5 实验结果分析

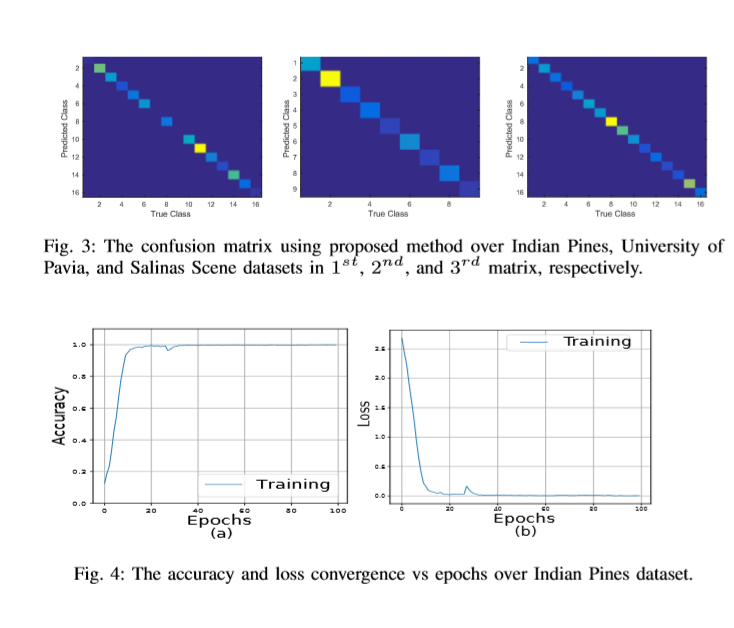
作者使用了Overall Accuracy (OA)， Average Accuracy (AA) and Kappa Coefficient (Kappa)三个评价指标来判断HSI的分类性能。其中OA表示测试样本总数中正确分类的样本数;AA为分类分类准确率的平均值;和Kappa是一个统计测量的度量，它提供关于在地面真实地图和分类地图之间的一个强协议的相互信息。

从表二可以看出，混合算法在保持最小标准偏差的同时，在每个数据集上都优于所有的比较方法。

图3显示了混合网络在IP、UP和SA数据集上的HSI分类性能的混淆矩阵。

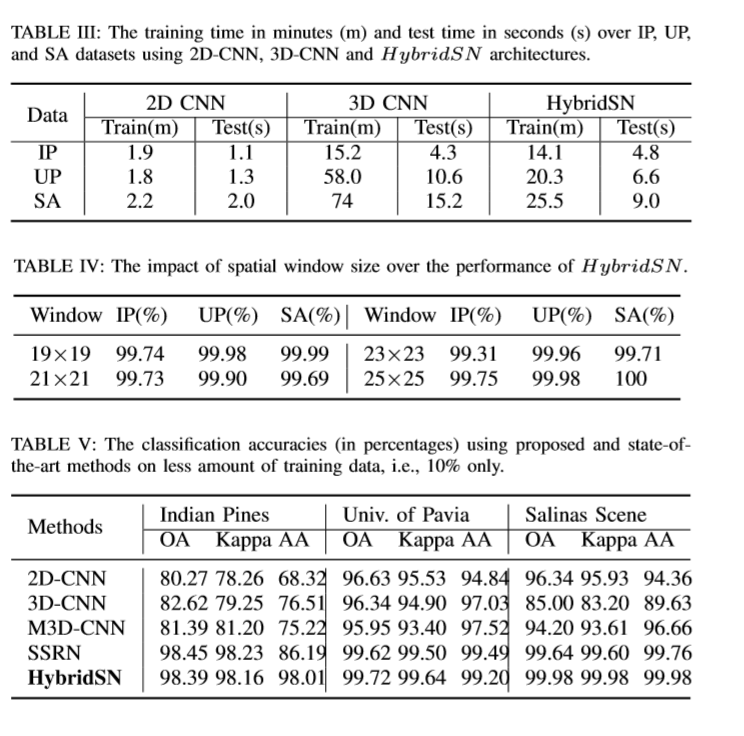
训练集和验证集100个epoch的准确性和损失收敛如图4所示。可以看出，收敛时间约为50个epoch，这表明作者的方法收敛速度较快。

混合动力网络模型的计算效率体现在训练和测试次数方面，如表3所示。

2.6 总结

这篇论文介绍了一种混合的3D和2D模型用于高光谱图像分类。本文提出的hybrid dsn模型是将空间光谱和光谱的互补信息分别以三维卷积和二维卷积的形式结合在一起。在三个基准数据集上的实验结果与最新方法进行了比较，验证了该方法的优越性。该模型比3D-CNN模型的计算效率更高。在小的训练数据上也显示出了优越的性能。

三、代码练习

三维卷积部分：

  • conv1：（1, 30, 25, 25）， 8个 7x3x3 的卷积核 ==>（8, 24, 23, 23）
  • conv2：（8, 24, 23, 23）， 16个 5x3x3 的卷积核 ==>（16, 20, 21, 21）
  • conv3：（16, 20, 21, 21），32个 3x3x3 的卷积核 ==>（32, 18, 19, 19）

接下来要进行二维卷积，因此把前面的 32*18 reshape 一下，得到 （576, 19, 19）

二维卷积部分：
（576, 19, 19） 64个 3x3 的卷积核，得到 （64, 17, 17）

接下来是一个 flatten 操作，变为 18496 维的向量，

接下来依次为256，128节点的全连接层，都使用比例为0.4的 Dropout，

最后输出为 16 个节点，是最终的分类类别数。

下面是 HybridSN 类的代码：

class HybridSN(nn.Module):
  def __init__(self):
    super(HybridSN, self).__init__()
    self.conv3d_1 = nn.Sequential(
        nn.Conv3d(1, 8, kernel_size=(7, 3, 3), stride=1, padding=0),
        nn.BatchNorm3d(8),
        nn.ReLU(inplace = True),
    )
    self.conv3d_2 = nn.Sequential(
        nn.Conv3d(8, 16, kernel_size=(5, 3, 3), stride=1, padding=0),
        nn.BatchNorm3d(16),
        nn.ReLU(inplace = True),
    ) 
    self.conv3d_3 = nn.Sequential(
        nn.Conv3d(16, 32, kernel_size=(3, 3, 3), stride=1, padding=0),
        nn.BatchNorm3d(32),
        nn.ReLU(inplace = True)
    )

    self.conv2d_4 = nn.Sequential(
        nn.Conv2d(576, 64, kernel_size=(3, 3), stride=1, padding=0),
        nn.BatchNorm2d(64),
        nn.ReLU(inplace = True),
    )
    self.fc1 = nn.Linear(18496,256)
    self.fc2 = nn.Linear(256,128)
    self.fc3 = nn.Linear(128,16)
    self.dropout = nn.Dropout(p = 0.4)

  def forward(self,x):
    out = self.conv3d_1(x)
    out = self.conv3d_2(out)
    out = self.conv3d_3(out)
    out = self.conv2d_4(out.reshape(out.shape[0],-1,19,19))
    out = out.reshape(out.shape[0],-1)
    out = F.relu(self.dropout(self.fc1(out)))
    out = F.relu(self.dropout(self.fc2(out)))
    out = self.fc3(out)
    return out
posted @ 2020-08-08 18:00  陳半仙  阅读(1198)  评论(0)  编辑  收藏  举报