【学习笔记】网络流
一些概念
\(\bf{\underline{网络}}\):是一个特殊的有向图 \(G=(V,E)\),它包含:
-
源点 \(s\),汇点 \(t\)\((s \ne t)\)。
-
每条边 \(e(u,v)\) 都有一个容量 \(c(u,v)\)。
\(\bf{\underline{流}}\):就像水流,把每条边想象成管道,流就是流过其中的水,从网络源点 \(s\) 流向汇点 \(t\),需要保证每条边上的流 \(f(u,v)\) 不超过其容量,其满足以下性质:
- \(\bf{\underline{容量限制}}\):\(f(u,v) \leq c(u,v)\)。
- \(\bf{\underline{流守恒}}\):除源点和汇点外,任意点的净流量为0。
\(\bf{\underline{净流量}}\):定义节点 \(u\) 的净流量 \(f(u)=\sum\limits_{v \in V}f(u,v)-\sum\limits_{v \in V}f(v,u)\)。
定义一个网络上的流 \(f\) 的流量 \(|f|=f(s)=-f(t)\)。
\(\bf{\underline{割}}\):令 \({S,T}\) 为 \(V\) 的划分(\(S\cup T\) 且 \(S\cap T=\varnothing\)),且 \(s\in S,t\in T\),则称 \({S,T}\) 为该网络的一个割,定义其容量 \(||S,T||=\sum\limits_{u\in S}\sum\limits_{v\in T}c(u,v)\)。
常见问题:
-
\(\bf{\underline{最大流问题}}\):找到给定网络的一个合适的流 \(f\),使得该流的流量尽可能大,称 \(f\) 为最大流。
-
\(\bf{\underline{最小割问题}}\):找到给定网络的一个合适的割 \({S,T}\),使得该割的容量尽可能小,称 \({S,T}\) 为最小割。
-
\(\bf{\underline{最小费用最大流问题}}\):给定网络,给定每条边一个费用 \(w(u,v)\),即单位流量通过该边所花费的代价,对所有可能的最大流,找出一条费用最小的,称为最小费用最大流。
网络最大流
Ford-Fulkerson 思想
Ford-Fulkerson 是网络流的一个重要思想,接下来的算法都是基于该思想的优化,弄明白了 Ford-Fulkerson 增广的原理,其他的就好说了。
先来几个概念:
\(\bf{\underline{增广路}}\):一条从 \(s\) 到 \(t\) 的剩余流量非空的路径,它是用来扩充网络最大流的。
\(\bf{\underline{残留网络}}\):令 \(c(u,v)\) 等于其剩余流量,然后把所有剩余流量为 \(0\) 的边删掉后的网络。
流程:
- 初始时所有边的流量均为 \(0\)。
- 增广:找到一条从 \(s\) 到 \(t\) 的简单路径,按照流的性质,找到这条路径上的最大流,更新每条边的残余容量,(可以等价于减少该边的容量,当该边容量减为 \(0\) 则说明该边已满流),更新残留网络。
- 重复步骤 \(2\),直到找不出一条路径。
但这样基于贪心的策略并不一定最优,原因是当前增广的路径会对以后的增广产生影响,如下图:
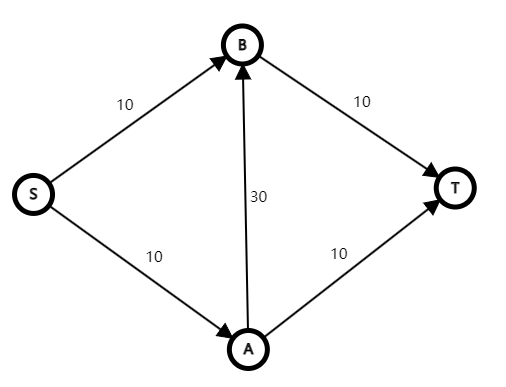
我们第一次增广路径 \(S \to A \to B \to T\),更新最大流为 \(10\)。
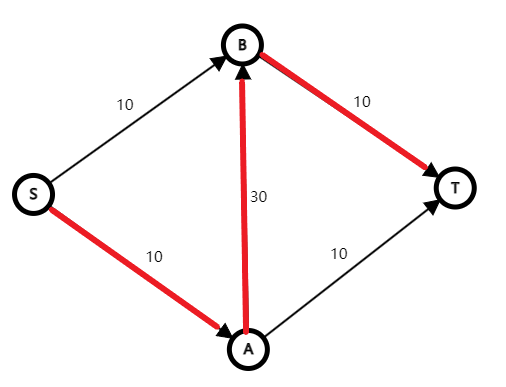
这样我们增广出来的最大流容量为 \(10\),但显然 \(S\to B\to T\) 和 \(S\to A\to T\) 能增广出来 \(20\)。
如何消除这种影响?
我们在对每条边补充一个反向边,初始时权值为 \(0\),对于每次增广的边,在减少原边容量的同时,增加反向边的容量,这样有啥用?
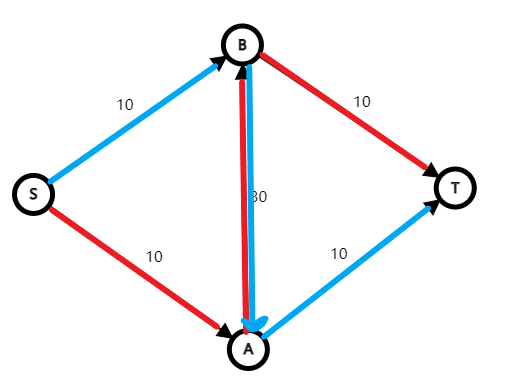
可以发现,这样我们就可以在原来的残留网络上再进行一次增广,得到最大流容量为 \(20\),其中 \((u,v)\) 这条边,正着流了一次,反着流了一次,相当于最大流根本不流经该边,实际上等于:
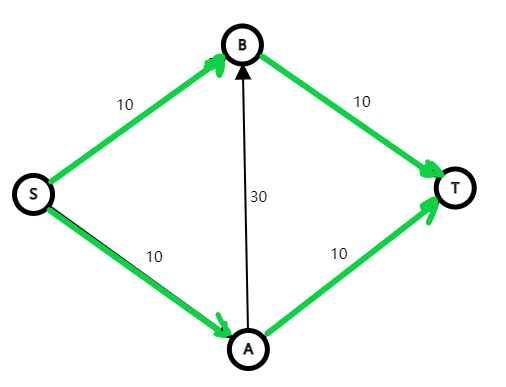
发现这样是遵循流量守恒的。
时间复杂度是值域级别,原因:
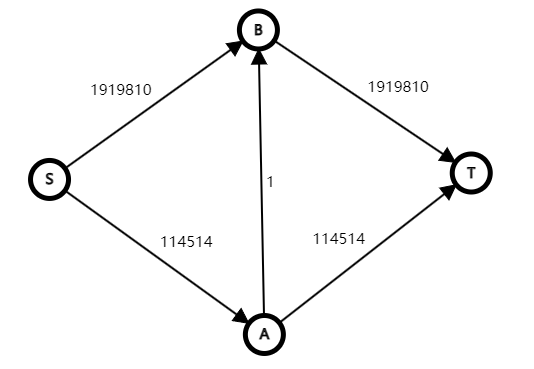
最大流是 \(114514+1919810=\) 不知道多少,然而如果我们每次只增广 \(A\to B\) 路径,就要增广不知道多少次。
Edmonds-Karp 算法
基于 Ford-Fulkerson 的优化,每次增广最短路,让复杂度有了保证。
每条边的长度为 \(1\),所以求的是 \(01\) 最短路,BFS 复杂度 \(\mathit{\Theta}(E)\)。
复杂度证明:
每次增广出的路径会使至少一条边的剩余容量减为零,称该边为关键边
因为每次找的是最短路,在残留网络中删除关键边,所以增广路的长度是单调不减的,且不超过 \(V\),所以最坏情况下每条边最多被增广 \(V\) 次,单次增广复杂度 \(E\),所以总复杂度 \(\mathit{\Theta}(VE^2)\)。
实现:
点击查看代码
struct node{
int w,v,nxt;
}e[M<<1];
int head[M],cnt=1;
il void add(int u,int v,int w){
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int n,m,s,t;
int pre[M],dis[M];
queue<int> q;
il int bfs(){
for(int i=1;i<=n;i++)pre[i]=0,dis[i]=1145141919;
q.push(s);
while(!q.empty()){
int x=q.front();q.pop();
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(pre[y]||y==s||!e[i].w)continue;
q.push(y);
dis[y]=min(dis[x],e[i].w);
pre[y]=i;
}
}
if(!pre[t])return -1;
return dis[t];
}
main(){
n=read(),m=read(),s=read(),t=read();
for(int i=1;i<=m;i++){
int u=read(),v=read(),w=read();
add(u,v,w);
add(v,u,0);
}
ll ans=0;
while(true){
int k=bfs();
if(k==-1)break;
ans+=k;
int now=t;
while(now!=s){
e[pre[now]].w-=k;
e[pre[now]^1].w+=k;
now=e[pre[now]^1].v;
}
}
cout<<ans;
return 0;
}
Dinic 算法
EK 算法在稠密图是 \(n^5\) 级别的,能不能继续优化?
我们发现 EK 每次bfs只能增广出一条增广路,所以慢了,能不能一次性找出多条。
Dinic 算法的思想就是一次找出所有最短路,全跑了。
按其DFS深度将网络分层,然后一遍DFS跑完全图最短路,即只走跨层的边。
这样就复杂度就少了一个 \(E\),是 \(\mathit{\Theta}(VE)\) 的吗?不是,因为一个点会被经过多次。
两个优化:
-
对增广完的点剪枝:把剩余容量为 \(0\) 的点深度置为-1,说明该点无法在当前分层图上做出贡献,就不要再访问它了。
-
当前弧优化:记录数组 \(now[u]\) 改变枚举边的起点。对于点 \(u\),当增广到它的第 \(i\) 条边时,前 \(i-1\) 条边到汇点的流量已经被用完了,访问了也没用,就不用再访问了,它保证了每条边最多只会被访问一次。
Dinic时间复杂度上限是 \(\mathit{\Theta}(V^2E)\) 的,证明见 OI wiki ,我不会。
但实际上并不会跑满,出题人只要有 ma 就不会卡。。
实现:
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define il inline
#define ll long long
#define int long long
il ll read(){
ll x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int M=5010;
const ll inf=1ll<<60;
struct node{
int v,nxt;
ll w;
}e[M<<1];
int head[M],cnt=1;
il void add(int u,int v,ll w){
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int n,m,s,t;
int dep[M],now[M];
queue<int> q;
il bool bfs(){
while(!q.empty())q.pop();
for(int i=1;i<=n;i++)dep[i]=-1;
dep[s]=0;
q.push(s);
now[s]=head[s];
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(e[i].w>0&&dep[y]==-1){
q.push(y);
now[y]=head[y];
dep[y]=dep[x]+1;
if(y==t)return 1;
}
}
}
return 0;
}
int dfs(int x,ll sum){
if(x==t)return sum;
ll k,flow=0;
for(int i=now[x];i&∑i=e[i].nxt){
now[x]=i;
int y=e[i].v;
if(e[i].w>0&&(dep[y]==dep[x]+1)){
k=dfs(y,min(sum,e[i].w));
if(k==0)dep[y]=-1;
e[i].w-=k;
e[i^1].w+=k;
flow+=k;
sum-=k;
}
}
return flow;
}
main(){
n=read(),m=read(),s=read(),t=read();
for(int i=1;i<=m;i++){
int u=read(),v=read();
ll w=read();
add(u,v,w);
add(v,u,0);
}
ll ans=0;
while(bfs())ans+=dfs(s,inf);
cout<<ans;
return 0;
}
最小割
\(\bf{\underline{最大流最小割定理}}\):最大流流量等于最小割容量:\(|f|=||{S,T}||\)
证明:
首先跑完最大流剩余容量为 \(0\) 的边全部割掉就是一个合法的割,若 \(s\) 和 \(t\) 仍然联通,则还可以继续增广,显然该流不是最大流,所以最小割的容量肯定不会大于最大流,否则该流一定不是最大流。即 \(|f|\le ||{S,T}||\)。
若最小割小于最大流,则跑完最小割的所有割边增广出来的流量小于最大流,那就不会有更多的流量流到汇点,所以该最大流不合法,所以 \(|f|=||{S,T}||\)。
所以直接套用最大流的算法就行了。
最小费用最大流
思路:
每次增广时增广当前费用最少的流,一直增广下去,直到找不到路径,此时得到的就是最小费用最大流。
这个是容易理解的,每次我们会增广一个固定的流量,选择一条总费用最少的路径,我们的花费就是最小的,这样我们的总花费也是最小的。
所以费用流问题就是最大流问题和最短路径问题的结合,这里介绍 dinic+SPFA 的方法,即 ZKW 费用流。
ZKW 费用流
关于spfa,它活了
为啥我们要选择 SPFA 来跑最短路,dij 它不香吗?我们在建立反向边时,其费用势必会出负数,而 dij 无法处理负边权,所以我们的 SPFA 它就活了。
将 Dinic 的 BFS 求最短路换成 SPFA 基本上就是套用 Dinic 的模板。
注意在 DFS 时该图不一定为DAG,可能在一个环上死循环,需要记一个 \(vis\) 数组。
说白了其实就是 EK 的一个常数优化。
实现:
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define il inline
#define ll long long
il ll read(){
ll x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int M=5e4+10;
const int N=5e3+10;
const ll inf=1ll<<50;
struct node{
int v,nxt;
ll w,c;
}e[M<<1];
int head[N],cnt=1;
il void add(int u,int v,ll w,ll c){
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].c=c;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int n,m,s,t;
bool vis[N];
ll dis[N];
queue<int>q;
il bool SPFA(){
for(int i=1;i<=n;i++)vis[i]=false,dis[i]=inf;
while(!q.empty())q.pop();
dis[s]=0;
q.push(s);
vis[s]=true;
while(!q.empty()){
int x=q.front();
q.pop();
vis[x]=0;
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(!e[i].w||dis[y]<=dis[x]+e[i].c)continue;
dis[y]=dis[x]+e[i].c;
if(!vis[y]){
q.push(y);
vis[y]=1;
}
}
}
return dis[t]<inf;
}
ll dfs(int x,ll sum){
if(x==t)return sum;
ll flow=0;
vis[x]=1;
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(!vis[y]&&e[i].w>0&&(dis[y]==dis[x]+e[i].c)){
ll k=dfs(y,min(sum,e[i].w));
e[i].w-=k;
e[i^1].w+=k;
flow+=k;
sum-=k;
}
}
return flow;
}
main(){
n=read(),m=read(),s=read(),t=read();
for(int i=1;i<=m;i++){
int u=read(),v=read(),w=read(),c=read();
add(u,v,w,c);
add(v,u,0,-c);
}
ll ans=0,Ans=0;
while(SPFA()){
ll tmp=dfs(s,inf);
ans+=tmp;
Ans+=1ll*tmp*dis[t];
}
cout<<ans<<" "<<Ans;
return 0;
}
网络流建模
P2472 [SCOI2007] 蜥蜴
-
对于原来有的每一只蜥蜴,从源点向每一只蜥蜴所在的石柱连边,流量为 \(1\),表示只会在该石柱生成一只蜥蜴。
-
对于每一个石柱,将其拆成两个点,入点和出点,从入店向出点连一条流量为 \(a_i\) 的边,表示该石柱只能经过 \(a_i\) 次。
-
石柱和石柱之间,若欧几里得距离(不是曼哈顿距离) \(\le d\) 则连一条流量为 \(+\infty\) 的边,表示石柱之间可到达。
-
对于每一个石柱,若到边界的距离 \(\le d\),则往汇点连一条流量为 \(+\infty\) 的边,表示该石柱可以跳出边界。
然后跑最大流。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define il inline
il int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=2200;
const int M=41000;
const int inf=1ll<<30;
char ch[N][N];
int a[N][N],tot(0);
map<pair<int,int>,int> id;
pair<int,int> pos[M];
il double get_dis(int x,int y){
return sqrt(1.0*(pos[x].first-pos[y].first)*(pos[x].first-pos[y].first)+1.0*(pos[x].second-pos[y].second)*(pos[x].second-pos[y].second));
}
struct node{
int v,w,nxt;
}e[M<<3];
int head[M],cnt(1);
il void add(int u,int v,int w){
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int n,m,d,s,t;
namespace Dinic{
int dep[M],now[M];
queue<int> q;
il bool bfs(){
while(!q.empty())q.pop();
for(int i=1;i<=2*tot+2;i++)dep[i]=-1;
dep[s]=0;
q.push(s);
now[s]=head[s];
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(e[i].w>0&&dep[y]==-1){
q.push(y);
now[y]=head[y];
dep[y]=dep[x]+1;
if(y==t)return 1;
}
}
}
return 0;
}
int dfs(int x,int sum){
if(x==t)return sum;
int k,flow=0;
for(int i=now[x];i&∑i=e[i].nxt){
now[x]=i;
int y=e[i].v;
if(e[i].w>0&&(dep[y]==dep[x]+1)){
k=dfs(y,min(sum,e[i].w));
if(k==0)dep[y]=-1;
e[i].w-=k;
e[i^1].w+=k;
flow+=k;
sum-=k;
}
}
return flow;
}
int main(){
int ans=0;
while(bfs())ans+=dfs(s,inf);
return ans;
}
}
int main(){
n=read(),m=read(),d=read();
for(int i=1;i<=n;i++)cin>>ch[i]+1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
a[i][j]=ch[i][j]-'0';
if(a[i][j]>0){
id[{i,j}]=++tot;
pos[tot]={i,j};
}
}
s=2*tot+1,t=2*tot+2;
for(int i=1;i<=tot;i++){
if(pos[i].first<=d||pos[i].second<=d||(n+1-pos[i].first<=d)||(m+1-pos[i].second<=d)){
add(i+tot,t,inf);
add(t,i+tot,0);
}
}
for(int i=1;i<=tot;i++){
for(int j=1;j<=tot;j++){
if(i==j)continue;
if(get_dis(i,j)<=1.0*d){
add(i+tot,j,inf);
add(j,i+tot,0);
}
}
}
for(int i=1;i<=tot;i++){
add(i,i+tot,a[pos[i].first][pos[i].second]);
add(i+tot,i,0);
}
int sum=0;
for(int i=1;i<=n;i++)cin>>ch[i]+1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(ch[i][j]=='L'){
sum++;
int to=id[{i,j}];
// cout<<s<<"->"<<to<<endl;
add(s,to,1);
add(to,s,0);
}
int tot=Dinic::main();
cout<<sum-tot;
return 0;
}
[SDOI2015] 星际战争
二分答案 \(T\),判断在 \(T\) 的时间内的答案是否大于等于所有装甲值之和。
对于一个已知的时间 \(T\),如下建图:
-
对于每一个激光武器,从源点向该武器连一条容量为 \(T\times b_i\),表示在 \(T\) 时间内造成最多能造成的伤害。
-
对于每一个机器人,向汇点连一条容量为 \(a_i\) 的边,表示该机器人被摧毁需要的伤害。
-
将每一个激光武器向它能攻击到的机器人连一条容量为 \(+\infty\) 的边,表示可以攻击。
然后跑最大流。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define il inline
#define ll long long
il int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N=60;
const int M=10000;
const double eps=1e-4;
const int inf=1ll<<30;
int a[N],b[N];
bool mp[N][N];
struct node{
int v,nxt;
double w;
}e[M<<1];
int head[M],cnt(1);
il void add(int u,int v,double w){
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int n,m,s,t,tot;
namespace Dinic{
int dep[M],now[M];
queue<int> q;
bool bfs(){
while(!q.empty())q.pop();
for(int i=1;i<=n+m+2;i++)dep[i]=inf;
dep[s]=0;
q.push(s);
now[s]=head[s];
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(e[i].w>eps&&dep[y]==inf){
q.push(y);
dep[y]=dep[x]+1;
now[y]=head[y];
if(y==t)return 1;
}
}
}
return 0;
}
double dfs(int x,double sum){
if(x==t)return sum;
double flow=0;
for(int i=now[x];i&&sum>eps;i=e[i].nxt){
now[x]=i;
int y=e[i].v;
if(e[i].w>eps&&dep[y]==dep[x]+1){
double k=dfs(y,min(sum,e[i].w));
if(k<eps)dep[y]=inf;
e[i].w-=k;
e[i^1].w+=k;
flow+=k;
sum-=k;
}
}
return flow;
}
double main(){
double ans=0;
while(bfs())ans+=dfs(s,inf);
return ans;
}
}
bool Testify(double T){
for(int i=1;i<=n+m+2;i++)head[i]=0;
cnt=1;
for(int i=1;i<=m;i++){
add(s,i,1.0*T*b[i]);
add(i,s,0);
}
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
if(mp[i][j]){
add(i,j+m,inf);
add(j+m,i,0);
}
for(int i=1;i<=n;i++){
add(i+m,t,1.0*a[i]);
add(t,i+m,0);
}
double ans=Dinic::main();
return (ans>=tot-eps);
}
int main(){
n=read(),m=read();
for(int i=1;i<=n;i++)a[i]=read(),tot+=a[i];
for(int i=1;i<=m;i++)b[i]=read();
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
mp[i][j]=read();
s=n+m+1,t=n+m+2;
double L=0,R=50000.0,mid;
while(R-L>eps){
mid=L+(R-L)/2;
if(Testify(mid))R=mid;
else L=mid;
}
printf("%.5f\n",L);
return 0;
}
P4311 士兵占领
考虑先给所有可以放的位置放上士兵,再尽可能多的地删除多余的士兵,这不就是最大流吗。
我们设 \(R_l(i)\) 表示第 \(i\) 行能放的位置数, \(R_c(i)\) 表示第 \(i\) 列能放的位置数。
-
从源点向每一行连一条容量为 \(R_l(i)-L_i\) 的边,表示该行最多能删除的士兵数。
-
行和列之间如果交点能放士兵则连一条容量为 \(1\) 的边,表示该位置只能被删除一次。
-
从每一列向汇点连一条容量为 \(R_c(i)-C_i\) 的边,表示该列最多能删除的士兵数。
然后跑最大流。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define il inline
#define ll long long
il int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int M=110;
const int inf=1ll<<30;
int a[M],b[M],aa[M],bb[M];
bool mp[M][M];
int del[M][M];
struct node{
int v,nxt,w;
}e[M*M<<1];
int head[2*M],cnt(1);
il void add(int u,int v,int w){
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int n,m,k,s,t;
namespace Dinic{
int dep[2*M],now[2*M];
queue<int> q;
il bool bfs(){
while(!q.empty())q.pop();
for(int i=1;i<=n+m+2;i++)dep[i]=inf;
q.push(s);
dep[s]=0;
now[s]=head[s];
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(e[i].w>0&&dep[y]==inf){
q.push(y);
dep[y]=dep[x]+1;
now[y]=head[y];
if(y==t)return 1;
}
}
}
return 0;
}
int dfs(int x,int sum){
if(x==t)return sum;
int flow=0;
for(int i=now[x];i;i=e[i].nxt){
now[x]=i;
int y=e[i].v;
if(e[i].w>0&&dep[y]==dep[x]+1){
int k=dfs(y,min(sum,e[i].w));
if(k==0)dep[y]=inf;
e[i].w-=k;
e[i^1].w+=k;
flow+=k;
sum-=k;
}
}
return flow;
}
int main(){
int ans=0;
while(bfs())ans+=dfs(s,inf);
return ans;
}
}
int main(){
m=read(),n=read(),k=read();
int tot=n*m-k;
for(int i=1;i<=m;i++)a[i]=read();
for(int i=1;i<=n;i++)b[i]=read();
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
mp[i][j]=1;
while(k--){
int u=read(),v=read();
mp[u][v]=0;
aa[u]++;
bb[v]++;
}
s=n+m+1,t=n+m+2;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(!mp[i][j])continue;
add(i,j+m,1);
add(j+m,i,0);
}
}
for(int i=1;i<=m;i++){
int val=n-aa[i];
if(a[i]>val)return !puts("JIONG!");
add(s,i,val-a[i]);
add(i,s,0);
}
for(int i=1;i<=n;i++){
int val=m-bb[i];
if(b[i]>val)return !puts("JIONG!");
add(i+m,t,val-b[i]);
add(t,i+m,0);
}
cout<<tot-Dinic::main();
}
P3191 [HNOI2007] 紧急疏散EVACUATE
还是二分答案,考虑怎么求一个时间内最多能疏散的人数。
发现这道题比较难搞的地方是每个门每个时间只能疏散一个人。
这种情况下我们有一个套路就是把这个门拆了,每个时间对应一个门(这个门在另一个时间就不是它自己了)
-
从源点向每个人连容量为 \(1\) 边。
-
每个人向能到达的门连容量为 \(1\) 的边。
-
每个时间的每个门向汇点连一条容量为 \(1\) 的边,表示一个门一个时间只能疏散一个人。
-
每个门向自己之后的一个时间的门连一条容量为 \(+\infty\) 的边,表示每个人到达门后还可以等到之后的某个时间再走。
然后跑最大流。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define il inline
#define ll long long
il int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int M=30;
const int N=M*M;
const int V=N;
const int maxe=1e6+10;
const int inf=1ll<<30;
struct node{
int v,nxt,w;
}e[maxe<<1];
int head[maxe],cnt(1);
il void add(int u,int v,int w){
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int n,m,S,T;
char ch[M][M];
namespace Dinic{
int dep[maxe],now[maxe];
il bool bfs(){
queue<int> q;
for(int i=1;i<=T;i++)dep[i]=inf;
dep[S]=0;
q.push(S);
now[S]=head[S];
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(e[i].w>0&&dep[y]==inf){
now[y]=head[y];
dep[y]=dep[x]+1;
q.push(y);
if(y==T)return 1;
}
}
}
return 0;
}
int dfs(int x,int sum){
if(x==T)return sum;
int flow=0;
for(int i=now[x];i;i=e[i].nxt){
int y=e[i].v;
if(e[i].w>0&&dep[y]==dep[x]+1){
int k=dfs(y,min(sum,e[i].w));
if(k==0)dep[y]=inf;
e[i].w-=k;
e[i^1].w+=k;
flow+=k;
sum-=k;
}
}
return flow;
}
int main(){
int ans=0;
while(bfs()){
ans+=dfs(S,inf);
}
return ans;
}
}
int dcnt(0),tot(0),dis[N][N];
bool vis[M][M];
map<pair<int,int>,int>id,doorid;
pair<int,int> pos[N],doorpos[N];
il bool Testify(int tim){
for(int i=1;i<=T;i++)head[i]=0;
cnt=1;
for(int i=1;i<=dcnt;i++){
for(int j=1;j<=min(V,tim);j++){
add(tot+2*(i-1)*V+j,tot+2*(i-1)*V+V+j,1);
add(tot+2*(i-1)*V+V+j,tot+2*(i-1)*V+j,0);
add(tot+2*(i-1)*V+V+j,T,inf);
add(T,tot+2*(i-1)*V+V+j,0);
}
for(int j=2;j<=V;j++){
add(tot+2*(i-1)*V+j-1,tot+2*(i-1)*V+j,inf);
add(tot+2*(i-1)*V+j,tot+2*(i-1)*V+j-1,0);
}
for(int j=1;j<=tot;j++){
if(dis[i][j]<=tim){
add(j,tot+2*(i-1)*V+dis[i][j],1);
add(tot+2*(i-1)*V+dis[i][j],j,0);
}
}
}
for(int i=1;i<=tot;i++){
add(S,i,1);
add(i,S,0);
}
int tmp=Dinic::main();
return tmp>=tot;
}
void bfs(int stx,int sty,int now){
queue<pair<pair<int,int>,int>>q;
q.push({{stx,sty},0});
while(!q.empty()){
pair<pair<int,int>,int> tp=q.front();
q.pop();
int x=tp.first.first,y=tp.first.second,dep=tp.second;
if(vis[x][y])continue;
vis[x][y]=1;
if(ch[x][y]=='.')dis[now][id[{x,y}]]=dep;
if(x<n&&ch[x+1][y]=='.')q.push({{x+1,y},dep+1});
if(x>1&&ch[x-1][y]=='.')q.push({{x-1,y},dep+1});
if(y<m&&ch[x][y+1]=='.')q.push({{x,y+1},dep+1});
if(y>1&&ch[x][y-1]=='.')q.push({{x,y-1},dep+1});
}
}
int main(){
n=read(),m=read();
for(int i=1;i<=n;i++)cin>>ch[i]+1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(ch[i][j]=='.'){
++tot;
pos[tot]={i,j};
id[{i,j}]=tot;
}
else if(ch[i][j]=='D'){
++dcnt;
doorpos[dcnt]={i,j};
doorid[{i,j}]=dcnt;
}
}
}
if(dcnt==0)return !puts("impossible");
for(int i=1;i<=dcnt;i++){
for(int j=1;j<=tot;j++)dis[i][j]=inf;
}
S=tot+2*V*dcnt+1;T=S+1;
for(int i=1;i<=dcnt;i++){
memset(vis,0,sizeof(vis));
bfs(doorpos[i].first,doorpos[i].second,i);
}
int L=0,R=400,ans=0;
while(L<=R){
int mid=(L+R)>>1;
if(Testify(mid)){
R=mid-1;
ans=mid;
}
else L=mid+1;
}
cout<<ans;
return 0;
}
本文来自博客园,作者:CCComfy,转载请注明原文链接:https://www.cnblogs.com/cccomfy/p/17793009.html


 喜了,恼了,喜恼了,恼喜了,喜恼喜了,恼喜恼了,了了了。
喜了,恼了,喜恼了,恼喜了,喜恼喜了,恼喜恼了,了了了。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号