CSP模拟58联测20 题解
T1 回忆旅途的过往
因为每个砝码都可以使用无限次,所以我们只需要关注区间内数的种类。
发现所有出现的数不会超过 \(10\) 种,考虑状压。二进制每一位表示该位表示的数是否出现。
预处理出 \(f_{S,x}\) 表示状态 \(S\) 是否可以称出质量 \(x\),对于新出现的数 \(x\),标号为 \(id\),则 \(f_{S}=f_{S-(1<<id)}\),\(f_{S,i}=f_{S,i}|f_{S,i-x}\), \(O(2^{10}m)\) 转移即可。
区间操作使用线段树维护,每个叶子节点维护对应区间的二进制状态,\(push up\) 为 \(t_k=t_{k<<1}|t_{k<<1|1}\)
Code
#include <bits/stdc++.h>
using namespace std;
#define il inline
#define ll long long
namespace Testify{
il int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
il void write(ll x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
il void Write(ll x){write(x);puts("");}
il void writE(ll x){write(x);putchar(' ');}
}
using namespace Testify;
#define M 1000050
#define N 100050
int n,m,q;
int a[M];
int vis[M];
// int ans[1030][M],id(0);
bitset<N>ans[1030];
int id(0);
namespace Segment_Tree{
int sum[M<<2],tag[M<<2];
il void push_up(int k){
sum[k]=sum[k<<1]|sum[k<<1|1];
}
il void build(int k,int l,int r){
tag[k]=-1;
if(l==r){
sum[k]=(1<<vis[a[l]]);
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
push_up(k);
}
il void add_tag(int k,int x){
tag[k]=x;
sum[k]=x;
}
il void push_down(int k){
if(tag[k]==-1)return;
add_tag(k<<1,tag[k]);
add_tag(k<<1|1,tag[k]);
tag[k]=-1;
}
void update(int k,int l,int r,int L,int R,int x){
if(L<=l&&r<=R){
add_tag(k,x);
return;
}
push_down(k);
int mid=(l+r)>>1;
if(L<=mid)update(k<<1,l,mid,L,R,x);
if(R>mid)update(k<<1|1,mid+1,r,L,R,x);
push_up(k);
}
int query(int k,int l,int r,int L,int R){
if(L<=l&&r<=R)return sum[k];
push_down(k);
int mid=(l+r)>>1;
int tmp=0;
if(L<=mid)tmp=query(k<<1,l,mid,L,R);
if(R>mid)tmp|=query(k<<1|1,mid+1,r,L,R);
return tmp;
}
}
void add_num(int x){
vis[x]=id++;
for(int i=(1<<(id-1));i<(1<<id);i++){
ans[i]=ans[i-(1<<(id-1))];
for(int j=x;j<=m;j++)ans[i][j]=ans[i][j]|ans[i][j-x];
}
}
signed main(){
n=read(),m=read(),q=read();
memset(vis,-1,sizeof(vis));
ans[0][0]=1;
for(int i=1;i<=n;i++){
a[i]=read();
if(vis[a[i]]==-1)add_num(a[i]);
}
Segment_Tree::build(1,1,n);
for(int i=1;i<=q;i++){
int opt=read(),l=read(),r=read(),x=read();
if(opt==1){
if(vis[x]==-1)add_num(x);
Segment_Tree::update(1,1,n,l,r,(1<<vis[x]));
}else{
if(ans[Segment_Tree::query(1,1,n,l,r)][x])puts("Yes");
else puts("No");
}
}
}
T2 牵着她的手
前置知识:拉格朗日插值
发现如果 \(x_1\) 到 \(x_n\) 的最大值等于 \(x_{n+1}\) 到 \(x_{n+m}\) 的最大值,那么序列一定合法,因为它们的最大值都等于整个矩阵的最大值。
考虑构造一个矩阵,最大值的行和最大值的列相交的那个格子填那个最大值,那一行和那一列其他位置填任意数,其他位置都填 \(1\)。
(注意其他位置不一定非要填1,对于每一种合法序列,都能构造出至少一个满足要求的矩阵,且其中一定包含其他位置全填 \(1\) 的矩阵,如序列 \(2,3,2,3\) 可以构造出满足要求的矩阵 \(\begin{matrix} 1 & 2 \\ 2 & 3\end{matrix}\) 和 \(\begin{matrix} 2 & 2 \\ 2 & 3\end{matrix}\),因为答案统计的是序列,所以它们只对答案贡献 \(1\) 次,所以我们只统计其他位置全填 \(1\) 的贡献,这样能保证该矩阵一定满足要求)
那么我们考虑枚举这个最大值 \(i\) ,没有最大值限制每一行可以选择 \(i\) 个数,\(n\) 行的方案数为 \(i^n\),为了保证存在最大值,还要减去不含最大值的方案数 \((i-1)^n\),列同理,则答案为
直接枚举可以过 \(80 \%\) 的数据
考虑优化,发现和式里面那个东西是关于 \(i\) 的 \(n+m\) 次多项式,整个式子就是一个 \(n+m+1\) 次多项式。设 \(f_x=\sum\limits_{i=1}^{x}(i^n-(i-1)^n)(i^m-(i-1)^m)\),可以先算出 \(f_1\) 到 \(f_{n+m+2}\) ,发现 \(i\) 的取值连续,使用拉格朗日插值可以 \(O(n)\) 算出 \(f_k\)。
Code
#include <bits/stdc++.h>
using namespace std;
#define il inline
#define ll long long
namespace Testify{
il int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
il void write(ll x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
il void Write(ll x){write(x);puts("");}
il void writE(ll x){write(x);putchar(' ');}
}
using namespace Testify;
const int M=200050;
const int mod=1e9+7;
ll y[M];
ll g[M],sum,inv[M];
il ll fast_pow(ll x,int a){
ll ans=1;
while(a){
if(a&1)ans=ans*x%mod;
x=x*x%mod;
a>>=1;
}
return ans;
}
signed main(){
int T=read();
g[0]=1;
for(int i=1;i<=200005;i++)g[i]=(g[i-1]*fast_pow(i,mod-2))%mod;
while(T--){
int n=read(),m=read(),k=read();
int len=n+m+2;
for(int i=1;i<=len;i++)
y[i]=(y[i-1]+((fast_pow(i,n)-fast_pow(i-1,n)+mod)%mod)*((fast_pow(i,m)-fast_pow(i-1,m)+mod)%mod)%mod)%mod;
if(k<=len){
Write(y[k]);
continue;
}
sum=1;
for(int i=1;i<=len;i++)sum=sum*((k-i+mod)%mod)%mod;
ll ans=0;
for(int i=1;i<=len;i++){
ll tmp=y[i];
tmp=tmp*sum%mod;
tmp=tmp*fast_pow(k-i,mod-2)%mod;
tmp=tmp*g[i-1]%mod;
tmp=tmp*g[len-i]%mod;
if((len-i)%2)tmp=(mod-tmp)%mod;
ans=(ans+tmp)%mod;
}
Write(ans);
}
}
T3 注视一切的终结
去掉所有重边后是一棵树,每条边选择一种颜色,使得两点简单路径上相邻边的颜色尽可能多的不同。
发现如果一条边有大于等于 \(3\) 种颜色,则这条边一定会有一种颜色和两边颜色都不同,所以都可以看成有 \(3\) 种颜色。
对于每次询问两点的简单路径需要 $ \log n$ 解决,考虑倍增。
设状态 \(f_{x,i,a,b}\) 表示从 \(x\) 点往上跳 \(2^i\) 步,路径上靠近 \(x\) 的一端为第 \(a\) 种颜色,另一端为第 \(b\) 种颜色时的最大权值,其中 \(a \leq 3 ,b \leq 3\),\(f_{x,0,a,b}=[col_a \ne col_b]\)。
转移时直接枚举 \(x\),\(y=fa_{x,i-1}\),\(z=fa_{x,i}\),颜色分别设为 \(a,b,c\),则转移为 \(f_{x,i,a,c} = \max\{f_{x,i-1,a,b}+f_{y,i-1,b,c}\}\)
那么对于要查询的点对 \(x,y\),先分别求出两点到 \(lca\) 的最大权值,这部分转移和上边类似。若其中一点为 \(lca\) 答案就是最大值,否则再枚举一遍 \(lca\) 处两条边的颜色,\(ans=\max\{cx_a+cy_b+[col_a \ne col_b]\}\)
Code
#include <bits/stdc++.h>
using namespace std;
#define il inline
namespace Testify{
il int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
il void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
il void Write(int x){write(x);puts("");}
}
using namespace Testify;
#define M 500010
#define N 1000010
struct node{
int w,v,nxt;
}e[N<<1];
int head[M],ecnt(0);
il void add(int u,int v,int w){
e[++ecnt].v=v;
e[ecnt].w=w;
e[ecnt].nxt=head[u];
head[u]=ecnt;
}
int dep[M],f[M][21],dp[M][21][4][4];
int cx[4],cy[4],cc[4];
bool vis[M];
int col[M][4],cnt[M];
void dfs1(int x,int fa){
vis[x]=1;
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(y==fa){
if(cnt[x]==3)continue;
bool yes=1;
for(int j=0;j<cnt[x];j++)
if(col[x][j]==e[i].w){yes=0;break;}
if(yes)col[x][cnt[x]++]=e[i].w;
}
else if(!vis[y])dfs1(y,x);
}
}
void dfs2(int x,int fa){
dep[x]=dep[fa]+1;
vis[x]=1;
f[x][0]=fa;
if(x!=1){
for(int a=0;a<cnt[x];a++)
for(int b=0;b<cnt[fa];b++)
dp[x][0][a][b]=(col[x][a]!=col[fa][b]);
}
for(int i=1;(1<<i)<=dep[x];i++){
f[x][i]=f[f[x][i-1]][i-1];
int y=f[x][i-1],z=f[x][i];
for(int a=0;a<cnt[x];a++)
for(int b=0;b<cnt[y];b++)
for(int c=0;c<cnt[z];c++)
dp[x][i][a][c]=max(dp[x][i][a][c],dp[x][i-1][a][b]+dp[y][i-1][b][c]);
}
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(y==fa||vis[y])continue;
dfs2(y,x);
}
}
int Lca(int x,int y){
if(dep[x]<dep[y])swap(x,y);
for(int i=20;i>=0;i--) if(dep[f[x][i]]>=dep[y])x=f[x][i];
if(x==y)return x;
for(int i=20;i>=0;i--) if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];
return f[x][0];
}
int jump(int x,int dis,int c[]){
int now=x;
for(int i=0;i<=20;i++)
if((dis>>i)&1){
memset(cc,0,sizeof(cc));
for(int a=0;a<cnt[now];a++)
for(int b=0;b<cnt[f[now][i]];b++)
cc[b]=max(cc[b],c[a]+dp[now][i][a][b]);
memcpy(c,cc,sizeof(cc));
now=f[now][i];
}
return now;
}
int main(){
int n=read(),m=read();
for(int i=1;i<=m;i++){
int u=read(),v=read(),w=read();
add(u,v,w);add(v,u,w);
}
dfs1(1,0);
for(int i=1;i<=n;i++)vis[i]=0;
dfs2(1,0);
int q=read();
while(q--){
for(int i=0;i<3;i++)cx[i]=cy[i]=0;
int x=read(),y=read();
int lca=Lca(x,y),fx,fy,ans=0;
if(x!=lca)fx=jump(x,dep[x]-dep[lca]-1,cx);
if(y!=lca)fy=jump(y,dep[y]-dep[lca]-1,cy);
if(x==lca){
for(int i=0;i<cnt[fy];i++)ans=max(ans,cy[i]);
}else if(y==lca){
for(int i=0;i<cnt[fx];i++)ans=max(ans,cx[i]);
}else{
for(int a=0;a<cnt[fx];a++)
for(int b=0;b<cnt[fy];b++)
ans=max(ans,cx[a]+cy[b]+(col[fx][a]!=col[fy][b]));
}
cout<<ans<<'\n';
}
}
T4 超越你的极限
感谢 APJifengc 提供的 hack 数据
前置芝士: Slope Trick 优化一类凸代价函数DP
30pts 树形DP
设 \(f_{i,x}\) 表示以 \(i\) 为根的子树,\(A_i=x\) 的权值最大和。
转移枚举权值 \(j\)
给 \(f\) 数组记前缀 \(\max\) 可以优化掉 \(k\),复杂度 \(n^2\)。
30pts Code
ll dp[1050][1050];
int w[M];
void dfs(int x,int fa){
int mn=1000;
for(int i=head[x];i;i=e[i].nxt) {
int y=e[i].v;
if(y!=fa)dfs(y,x);
mn=min(mn,e[i].w);
}
for(int val=0;val<=mn;val++){
ll res=0;
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(y==fa)continue;
res+=dp[y][e[i].w-val];
}
dp[x][val]=max(dp[x][val],res+(ll)w[x]*val);
}
for(int i=1;i<=mn;i++)dp[x][i]=max(dp[x][i-1],dp[x][i]);
for(int i=mn+1;i<=1000;i++)dp[x][i]=dp[x][i-1];
}
signed main(){
int n=read();
for(int i=1;i<=n;i++)w[i]=read();
for(int i=1;i<n;i++){
int u=read(),v=read(),w=read();
add(u,v,w);
add(v,u,w);
}
dfs(1,0);
cout<<dp[1][1000]<<endl;
}
70pts 复杂度错误的Slope Trick
网上唯一能找到的题解复杂度还是错的
思路和正解是一样的,但是实现的复杂度错了。
我们设 \(F_i(x)=f_{i,x}\),\(G_i(x)=\max\limits_{k\leq z_i-x}F_i(k)\),把转移方程写成函数的形式:
在使用 slope trick 之前,我们需要先证明 \(F_i\) 和 \(G_i\) 是分段一次凸函数:
对于叶子节点,\(F_i(x)=w_i\times x\) 是一次函数。
对于 \(G_i(x)\) ,对于 \(k\leq z_i-x\)这部分,我们先处理 \(G_i(z_i-x)=\max\limits_{k\leq x}F_i(k)\) ,这是个前缀最大值,则图像一定是先斜率由正变为 \(0\) 再不变的函数:
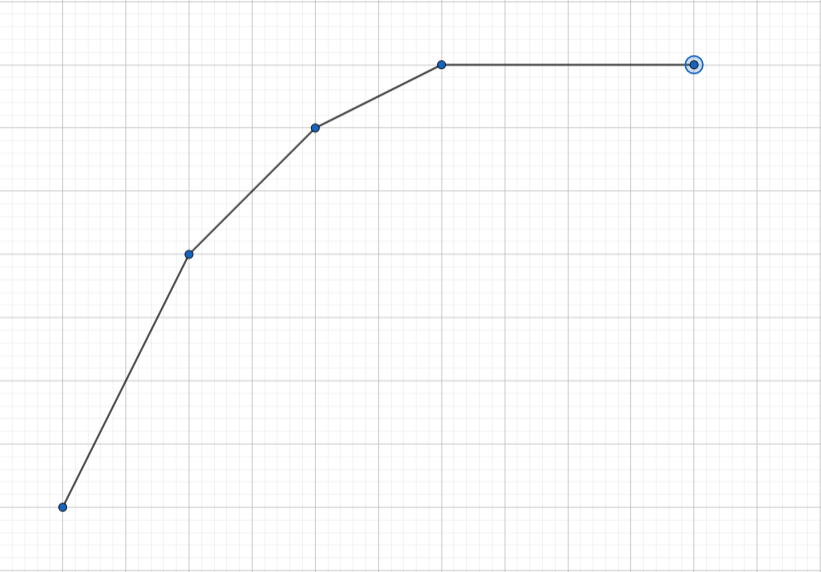
则 \(G_i(x)\) 的图像就是 \(G_i(z_i-x)\) 的图像关于 \(x=\frac{z_i}{2}\) 对称:
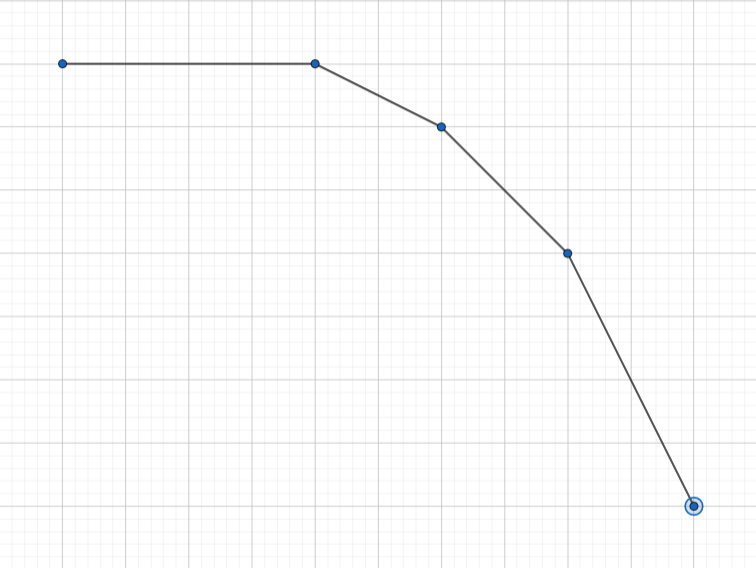
所以 \(G_i\) 也是凸函数,先给 \(G_i\) 求和,凸函数加凸函数还是凸函数,然后再加上一个 \(w_i\times x\) 一次函数,凸函数加一次函数还是凸函数,所以 \(F_i\) 为凸函数。
然后就证完了。
所以这个转移实质上就是维护一个凸函数的四种变化:
- 求一个凸函数的前缀 \(\max\)
- 将一个凸函数关于 \(\frac{z_i}{2}\) 翻转
- 几个凸函数相加
- 一个凸函数加上一个斜率为 \(w_i\) 的一次函数
我们给每一个节点开一个 map 来维护每个分段点的斜率变化量,即后缀差分,维护每个节点的斜率最小值 \(mn_i\) 和斜率最大值 \(mx_i\)(因为你需要支持翻转操作)。
- 对于前缀 \(\max\) 操作,我们需要把所有斜率小于零的分段点的全部删除,对于斜率差分我们只需要判断 \(mn_i\) 是否小于零,不断删除最后一个元素并更新 \(mn_i\)。
- 对于反转与求和操作,令 \(mn_i=-mx_i\),\(mx_i=-mn_i\),\(F_i(x)+=G_j(z_{i,j}-x)\),其中 \(j \in son_i\)。
- 对于加一次函数操作,令 \(f_i(+\infty)+=w_i\),然后不断删除横坐标大于 \(z\) 的分段点,再更新剩下的最后一个点的斜率。
然后就转移完了。
发现通过这些不好直接维护出答案,但是我们可以找到每个节点的函数在哪里取到最值即决策点,因为你每个节点的函数都转化成了前缀 \(\max\)(根节点就现求一遍),所以此时你的决策点一定是最末尾那个分段点(函数是不降的),直接 \(dfs\) 到每个点累加到答案上。
70pts Code
int w[M];
const int inf=1e9;
map<int,int> mp[M];
int mn[M],mx[M];
il void solve(int x,int y,int w){
while(mp[x].size()){
auto now=*--mp[x].end();
if(now.first<=w)break;
mp[x].erase(now.first);
mp[x][w]+=now.second;
}
while(mp[y].size()){
auto now=*--mp[y].end();
if(now.first<=w)break;
mp[y].erase(now.first);
mp[y][w]+=now.second;
}
while(mn[y]<0){
auto now=prev(mp[y].end());
if(-mn[y]<now->second){
now->second+=mn[y];
mn[y]=0;
break;
}
mn[y]+=now->second;
mp[y].erase(now);
}
int sv=mx[y];mx[y]=-mn[y];mn[y]=-sv;
for(auto now:mp[y])mp[x][w-now.first]+=now.second;
mx[x]+=mx[y];mn[x]+=mn[y];
}
void dfs(int x,int fa){
mp[x][inf]=w[x];
mx[x]=w[x];
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(y==fa)continue;
dfs(y,x);
solve(x,y,e[i].w);
}
}
ll ans(0);
void dfs2(int x,int fa,int lim){
// cout<<mp[x].size()
ll tmp=min(prev(mp[x].end())->first,lim);
ans=ans+1ll*tmp*w[x];
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(y==fa)continue;
dfs2(y,x,e[i].w-tmp);
}
}
signed main(){
int n=read();
for(int i=1;i<=n;i++)w[i]=read();
for(int i=1;i<n;i++){
int u=read(),v=read(),w=read();
add(u,v,w);
add(v,u,w);
}
dfs(1,0);
while(mn[1]<0){
auto now=prev(mp[1].end());
if(-mn[1]<now->second){
now->second+=mn[1];
mn[1]=0;
break;
}
mn[1]+=now->second;
mp[1].erase(now);
}
dfs2(1,0,inf);
cout<<ans;
}
然后就做完了。
然后你发现你过不了最后一个点。
注意到你每次求和时是直接枚举儿子节点的 map 加到根节点上,这样如果不加启发式合并最坏情况下(比如说 \(siz_y\) 很大)复杂度会退化成 \(n^2\)。但是你为了保留子树信息不能启发式合并,所以不维护答案的做法就寄了。
100pts Slope Trick
思路和上面的一样,但是改用平衡树维护答案,也就是维护 \(\sum A_i\times x\) 的最大值。
对于每个点我们需要:
-
维护从子树转移过来的答案 \(s1\),全局斜率加标记 \(s2\),关于 \(\frac{n}{2}\) 翻转的 \(n\) 。
-
用平衡树维护出来 \(\sum p_i\) 即斜率和 \(sum1\),\(\sum p_i\times x_i\) 即每个点的斜率乘横坐标之和 \(sum2\)。
-
给平衡树维护区间翻转标记 \(rev\) 和平移标记 \(tag\)。
这样我们删除操作就直接在平衡树里删,求和操作直接在平衡树里合并,翻转和全局加操作直接维护标记。
关于翻转的那个式子:
先不管所有标记
即 \(s1=sum1 \times n -sum2\) 。
加上子树贡献和全局加标记,即 \(s1=s1+(s2+sum1)\times n-sum2\)。
然后直接转移,复杂度 \(O(n\log n)\)。
AC Code(盒的)
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ll long long
const int inf=1e9+1;
const int M=100050;
mt19937 gen(0);
il int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
il void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
struct EDGE{
int v,nxt,w;
}e[M<<1];
int head[M],cnt;
void add_edge(int u,int v,int w){
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int a[M];
namespace Treap{
struct node{
int l,r,rev,tag,key,val,pos;//rev:翻转标记 tag:区间平移标记
ll sum1,sum2;//sum1:sum{p_i} sum2:sum{x_i*p_i}
}t[M<<1];
int tot;
il void rev(int k){//整体反转打标记
t[k].rev^=1;
t[k].tag=-t[k].tag;
swap(t[k].l,t[k].r);
t[k].pos=-t[k].pos;
t[k].sum2=-t[k].sum2;
}
il void add(int k,int x){//整体平移
t[k].pos+=x;
t[k].tag+=x;
t[k].sum2+=x*t[k].sum1;
}
il void push_up(int k){
t[k].sum1=t[t[k].l].sum1+t[t[k].r].sum1+t[k].val;
t[k].sum2=t[t[k].l].sum2+t[t[k].r].sum2+1ll*t[k].val*t[k].pos;
}
il void push_down(int k){
if(t[k].rev){
if(t[k].l)rev(t[k].l);
if(t[k].r)rev(t[k].r);
t[k].rev=0;
}
if(t[k].tag){
if(t[k].l)add(t[k].l,t[k].tag);
if(t[k].r)add(t[k].r,t[k].tag);
t[k].tag=0;
}
}
void split(int k,int pos,int &L,int &R){
if(!k){L=0,R=0;return;}
push_down(k);
if(t[k].pos<pos){
L=k;
split(t[k].r,pos,t[L].r,R);
}
else{
R=k;
split(t[k].l,pos,L,t[R].l);
}
push_up(k);
}
int merge(int L,int R){
if(L==0||R==0)return L+R;
push_down(L);
push_down(R);
if(t[L].key<t[R].key) swap(L,R);
int a,b,c;
split(R,t[L].pos,a,b);
split(b,t[L].pos+1,b,c);
if(b) t[L].val+=t[R].val;
t[L].l=merge(t[L].l,a);
t[L].r=merge(t[L].r,c);
push_up(L);
return L;
}
il void add_point(int &k,int l,int r,int pos,int key,int val){
k=++tot;
t[tot].l=l,t[tot].r=r;
t[tot].pos=pos;t[tot].key=key;t[tot].val=val;
t[tot].sum1=val;t[tot].sum2=1ll*val*pos;
t[tot].rev=t[tot].tag=0;
}
void insert(int &k,int pos,int key,int val){
if(!k){
add_point(k,0,0,pos,key,val);
return;
}
push_down(k);
if(key>t[k].key){
int L,R;
split(k,pos,L,R);
add_point(k,L,R,pos,key,val);
push_up(tot);
k=tot;
return;
}
if(pos<t[k].pos)insert(t[k].l,pos,key,val);
else insert(t[k].r,pos,key,val);
push_up(k);
}
void del(int &k,int x){//加上x后斜率小于0的改成0
if(!k)return;
if(t[k].sum1+x>0)return;
push_down(k);
if(t[t[k].l].sum1+x<=0){
k=t[k].l;
del(k,x);
return;
}
x+=t[t[k].l].sum1;
if(t[k].val+x<=0){
t[k].val=-x;
t[k].r=0;
push_up(k);
return;
}
x+=t[k].val;
del(t[k].r,x);
push_up(k);
}
}
struct node{
int n,rt;
ll s1,s2;//s1:所有子节点的答案 s2:全局加标记
il void resize(int len){
if(n<len){
ll tmp=-(s2+Treap::t[rt].sum1);
Treap::insert(rt,n,gen(),tmp);
}
else if(n>len){
int L,R;
Treap::split(rt,len,L,R);
rt=L;
}
n=len;
}
il void rev(){
ll t1=s1+(s2+Treap::t[rt].sum1)*n-Treap::t[rt].sum2;
ll t2=s2+Treap::t[rt].sum1;
s1=t1;s2=-t2;
if(rt){
Treap::rev(rt);
Treap::add(rt,n);
}
}
il void merge(node &x){
s1+=x.s1;
s2+=x.s2;
rt=Treap::merge(rt,x.rt);
}
}f[M];
void dfs(int x,int fa){
int tmp=inf;
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(y==fa)continue;
tmp=min(tmp,e[i].w);
dfs(y,x);
}
f[x].n=tmp;
f[x].s2=a[x];
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(y==fa)continue;
f[y].resize(e[i].w);
f[y].rev();
f[y].resize(tmp);
f[x].merge(f[y]);
}
if(f[x].s2<=0) f[x].s2=f[x].rt=0;
else Treap::del(f[x].rt,f[x].s2);
}
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++)a[i]=read();
for(int i=1;i<n;i++){
int u=read(),v=read(),w=read();
add_edge(u,v,w);
add_edge(v,u,w);
}
dfs(1,0);
int t1=f[1].rt;
ll ans=f[1].s1+(f[1].s2+Treap::t[t1].sum1)*f[1].n-Treap::t[t1].sum2;
cout<<ans;
return 0;
}
写在后面
如果题解有哪里写错了欢迎指出喵
四道题目的名字分别为音乐游戏《Arcaea》(韵律源点,源神)4.0版本更新后FV曲包最终魔王曲《Testify》解锁的四个任务(部分)名称
-
回忆旅途的过往 :按顺序分别游玩v1.x、v2.x、v3.x、v4.x任意四个主线曲包中的乐曲各一首并通关。
-
牵着她的手:收藏已拥有的全部非联动对立,之后使用任意一名非联动对立游玩任意封面上只有对立的主线曲目
-
注视一切的终结:在Axiom of the End解锁页面停留4分钟。
-
超越你的极限:游玩任意曲目且结算时该曲潜力值大于个人潜力值。
参考资料:Arcaea中文维基

本文来自博客园,作者:CCComfy,转载请注明原文链接:https://www.cnblogs.com/cccomfy/p/17728753.html


 And testify~
And testify~

 浙公网安备 33010602011771号
浙公网安备 33010602011771号