数论

lateX!

排列组合

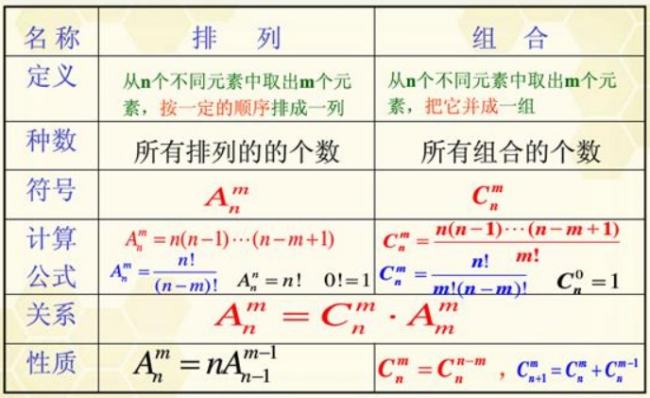
阶乘＆逆元

f[0]=g[0]=1;
int n=read(),k=read();
for(int i=1;i<=n;i++){
    f[i]=f[i-1]*i%mod;
    g[i]=g[i-1]*fast_pow(i,mod-2)%mod;
}

---------------------------------------

斯特林数

第二类斯特林数 -->被虐力
斯特林数应用
递推法：$$S(n,m)=S(n−1,m−1)+m\times S(n−1,m)$$
Code:

st[0][0]=1;
for(int i=1;i<=n;i++){
    for(int j=i;j<=m;j++){
        st[i][j]=(st[i-1][j-1]+j*st[i-1][j]%mod)%mod;
    }
}

边界：$$S(0,0)=0,S(1\sim{n},0)=1$$

\[\begin{aligned} x^k=\sum_{j=0}^k\{_j^k\}i^{\underline j}\\ \end{aligned} \]

下降幂

---

容斥与二项式反演

容斥原理（概念)
组合数学第六章 容斥原理应用
二项式定理(Sonnety)%%%

---

莫比乌斯反演

积性函数
狄利克雷前缀后缀差分
An_Account::莫比乌斯反演-让我们从基础开始
YSZ_y %%% 莫反证明 (mbwsfy)
整数分块

---

多项式与拉格朗日插值

拉格朗日插值的表达式:

\[f(x)=\sum_{i=1}^{n}y_i \prod_{j\ne i} \frac{x-x_j}{x_i-x_j} \]

横坐标是连续整数的拉格朗日插值:

\[f(x)=\sum_{i=1}^{n}y_i \frac{ \prod\limits_{j=1}^{n}(x-j)}{(x-i)(-1)^{n-i}(i-1)!(n-i)!} \]

OIwiki证明