佳佳的 Fibonacci 题解

佳佳的 Fibonacci 题解

题目：

---

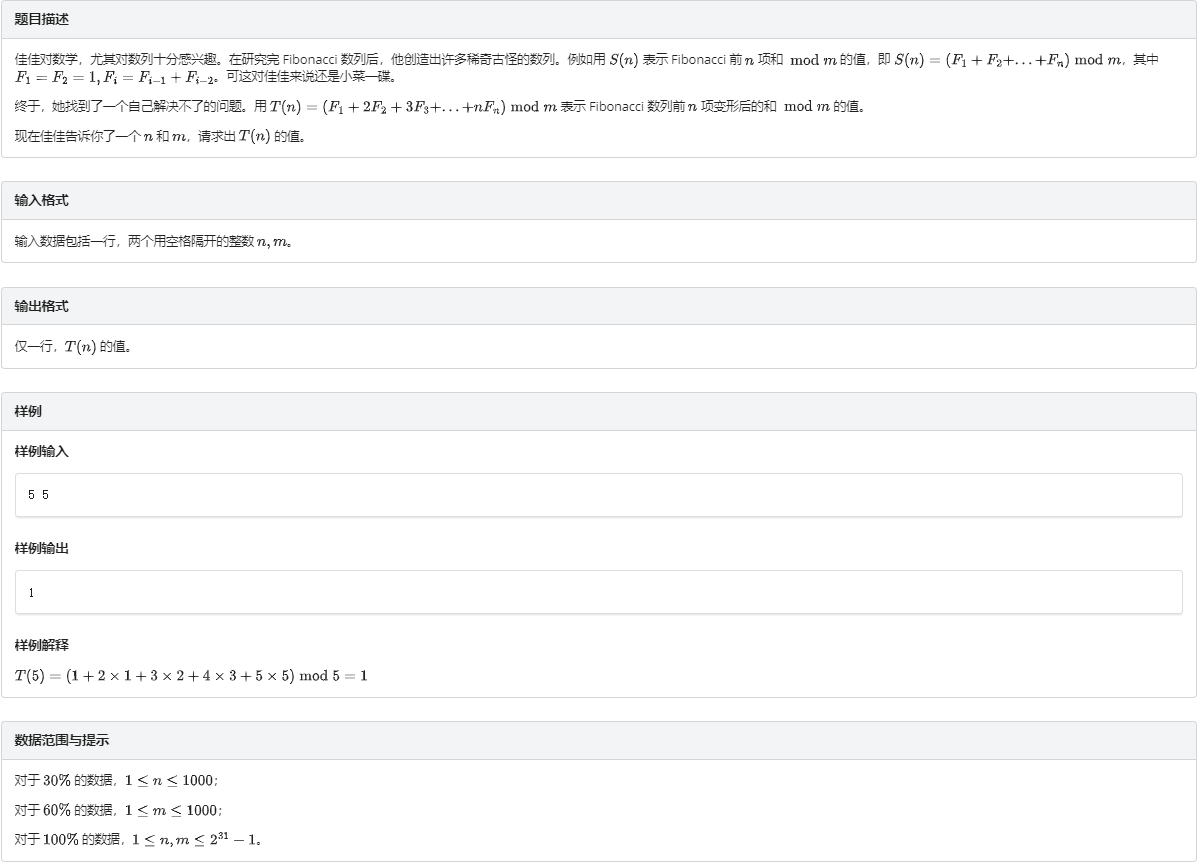
题解：

数据范围很大，暴力超时，考虑的是矩阵优化递推，关键是求出递推矩阵，然后结合矩阵快速幂求解
如何求解递推矩阵？
我们首先知道斐波那契的递推式：

$$f_i=f_i-1+f_i-2$$ ——>①

然后题目中给我们了T(n)的递推式：

$$T(n)=F_1+2F_2+3F_3+...+nF_n$$——>②

我们考虑从T(n-1)推得T(n)

$$T(n)=T(n-1)+n*F_n$$

由①的：

\[\begin{aligned} T(n)=T(n-1)+ n*(F_{n-1}+F_{n-2})\\ =T(n-1)+ n*F_{n-1} + n*F_{n-2}\\ \end{aligned}\]

我选择T[n-1],nF[n-1],nF[n-2],F[n-1],F[n-2]作为行向量
从而推出T[n],(n+1)F[n],(n+1)F[n-1],F[n],F[n-1];
我们现在需要找出底数矩阵A,它的规模应该是5*5的（显然

下面请填表：

	$$T(n-1)$$	$$nF_{n-1}$$	$$nF_{n-2}$$	$$F_{n-1} $$	$$F_{n-2}$$
$$T(n)$$
$$(n+1)F_n$$
$$(n+1)F_{n-1}$$
$$F_n$$
$$F_n-1$$

---

填完应该长这样：

	$$T(n-1)$$	$$nF_{n-1}$$	$$nF_{n-2}$$	$$F_{n-1}$$	$$F_{n-2}$$
$$T(n)$$	1	1	1	0	0
$$(n+1)*F_n$$	0	1	1	1	1
$$(n+1)*F_{n-1}$$	0	1	0	1	0
$$F_{n}$$	0	0	0	1	1
$$F_{n-1}$$	0	0	0	1	0

---

转置一下，就得到了矩阵A:

1	0	0	0	0
1	1	1	0	0
1	1	0	0	0
0	1	1	1	1
0	1	0	1	0

---

代码实现也很容易，注意A要转置（矩阵乘行向量）了解更多
给出代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define il inline
int n,mod;
il int read(){
    int x=0,f=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
il void write(int x){
    if(x<0)putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
    return;
}
struct mat{
    int m[10][10];
    mat(){
        memset(m,0,sizeof(m));
    }
};
mat operator*(const mat& a,const mat& b){
    mat c;
    for(int i=1;i<=5;i++)
        for(int j=1;j<=5;j++)
            for(int k=1;k<=5;k++)
                c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
    return c;
}
il mat fast_pow(int b){
    mat a,zero;
    a.m[1][1]=1;
    a.m[2][1]=1;
    a.m[2][2]=1;
	a.m[2][3]=1;
	a.m[3][1]=1;
    a.m[3][2]=1;
    a.m[4][2]=1;
    a.m[4][3]=1;
    a.m[4][4]=1;
	a.m[4][5]=1;
	a.m[5][2]=1;
    a.m[5][4]=1;
    zero.m[1][1]=3;
    zero.m[1][2]=3;
    zero.m[1][3]=3;
    zero.m[1][4]=1;
    zero.m[1][5]=1;
    while(b){
        if(b&1) zero=zero*a;
        b>>=1;
        a=a*a; 
        // for(int i=1;i<=5;i++){
        //     for(int j=1;j<=5;j++){
        //         cerr<<zero.m[i][j]<<" ";
        //     }
        //     cerr<<endl;
        // }
    }
    return zero;
}
main(void){
    n=read(),mod=read();
    if(n==1){
        cout<<1<<endl;
        return 0;
    }
    mat ans=fast_pow(n-2);
    write(ans.m[1][1]%mod);
}