贪吃的九头龙 题解

[NOI2002] 贪吃的九头龙

题目背景

传说中的九头龙是一种特别贪吃的动物。虽然名字叫“九头龙”，但这只是 说它出生的时候有九个头，而在成长的过程中，它有时会长出很多的新头，头的 总数会远大于九，当然也会有旧头因衰老而自己脱落。

题目描述

有一天，有 M 个脑袋的九头龙看到一棵长有 N 个果子的果树，喜出望外， 恨不得一口把它全部吃掉。可是必须照顾到每个头，因此它需要把 N 个果子分成 M 组，每组至少有一个果子，让每个头吃一组。

这M个脑袋中有一个最大，称为“大头”，是众头之首，它要吃掉恰好 K 个 果子 ，而 且 K 个果子中理所当然地应该包括唯一的一个 最大的果子。 果子由 N-1 根树枝连接起来，由于果树是一个整体，因此可以从任意一个果子出发沿着树枝 “走到”任何一个其他的果子。

对于每段树枝，如果它所连接的两个果子需要由不同的头来吃掉，那么两个 头会共同把树枝弄断而把果子分开；如果这两个果子是由同一个头来吃掉，那么 这个头会懒得把它弄断而直接把果子连同树枝一起吃掉。当然，吃树枝并不是很舒服的，因此每段树枝都有一个吃下去的“难受值”，而九头龙的难受值就是所 有头吃掉的树枝的“难受值”之和。

九头龙希望它的“难受值”尽量小，你能帮它算算吗？

例如图 1 所示的例子中，果树包含 8 个果子，7 段树枝，各段树枝的“难受 值”标记在了树枝的旁边。九头龙有两个脑袋，大头需要吃掉 4 个果子，其中必 须包含最大的果子。即 N=8，M=2，K=4：

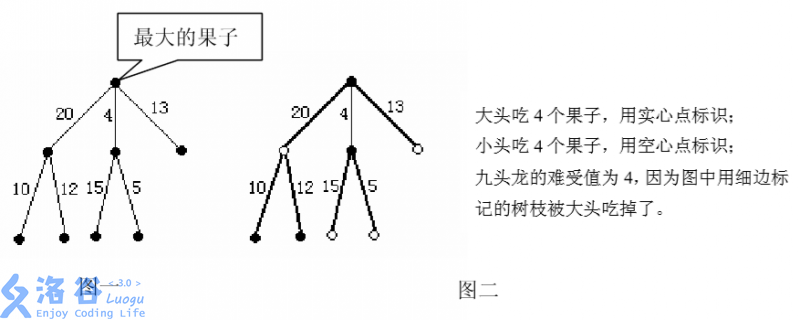
图一描述了果树的形态，图二描述了最优策略。

输入格式

输入文件 dragon.in 的第 1 行包含三个整数 N (1<=N<=300)，M (2<=M<=N)， K (1<=K<=N)。 N个果子依次编号 1,2,...,N，且 最大 的果子的 编 号 总 是 1。第 2 行到第 N 行描述了果树的形态，每行包含三个整数 a (1<=a<=N)，b (1<=b<=N)， c (0<=c<=\(10^5\))，表示存在一段难受值为 c 的树枝连接果子 a 和果子 b。

输出格式

输出文件 dragon.out 仅有一行，包含一个整数，表示在满足“大头”的要求 的前提下，九头龙的难受值的最小值。如果无法满足要求，输出-1。

样例 #1

样例输入 #1

8 2 4 
1 2 20 
1 3 4 
1 4 13 
2 5 10 
2 6 12 
3 7 15 
3 8 5

样例输出 #1

4

提示

该样例对应于题目描述中的例子。

题解（注释）

#include <bits/stdc++.h>
using namespace std;
#define M 500
struct edge{
    int from,to,next,w;
};
edge e[M];
int head[M],cnt;
int n,m,K;
int f[M][M][2];//以i为根的子树大头吃掉j个果子的难受度 0:不吃 1:吃
int g[M][M][2];//临时数组记录上一轮的结果
void add_edge(int u,int v,int w){//链式前向星存边好处理
    e[cnt].from=u;
    e[cnt].to=v;
    e[cnt].w=w;
    e[cnt].next=head[u];
    head[u]=cnt++;
}
void dp(int x){
    f[x][0][0]=0;//不分配显然是0
    f[x][1][1]=0;//分配一个且父节点吃儿子就不吃也是0
    for(int i=head[x];i;i=e[i].next){
        int y=e[i].to;
        dp(y);
        for(int i=0;i<=500;i++){//这是存储上一次更新结果的临时数组
            g[x][i][0]=f[x][i][0];
            g[x][i][1]=f[x][i][1];
        }
        memset(f[x],0x7f,sizeof(f[x]));
        for(int j=K;j>=0;j--){//可以当成01树状背包,但有临时数组正序逆序都行了（大概吧）
            for(int k=0;k<=j;k++){
                //int f[M][M][2];//以i为根的子树大头吃掉j个果子的难受度 0:不吃 1:吃
                f[x][j][1]=min(f[x][j][1],min(f[y][k][0]+g[x][j-k][1],f[y][k][1]+g[x][j-k][1]+e[i].w));
                //根节点分配j门课的状态由他的子节点们转移过来
                /*1.如果根节点吃果子，那么子节点可以吃可以不吃，吃的话就会加难受度，不吃的话不加，
                拿之前(f要初始化INF)更新过的状态（f[x][j][1]）和该状态（子节点分配k个即f[y][k][0/1],根节点就分配j-k个即f[x][j-k][1]）比较，若该状态更小，就更新f[x][j]
                注意j-k在之前的循环中会被更新，所以需要一个g数组记录上一轮的结果，保证更新到该状态时不会受影响
                因为父亲节点肯定是吃的所以不用考虑m==2的特殊情况
                */
                f[x][j][0]=min(f[x][j][0],min(f[y][k][1]+g[x][j-k][0],f[y][k][0]+g[x][j-k][0]+(m==2)*e[i].w));
                /*2.如果根节点不吃果子，那么子节点可以吃可以不吃，吃的话就不会加难受度，不吃的话{
                    <关于‘+(m==2)*e[i].w’的解释>
                    如果m>=3,不算大头其他头的个数大于等于2，一个吃父节点，一个吃子节点，不会再增加难受度
                    如果m==2,此时另一只头只能两个一起吃掉
                }
                拿之前(f要初始化INF)更新过的状态（f[x][j][0]）和该状态（子节点分配k个即f[y][k][0/1],根节点就分配j-k个即f[x][j-k][0]）比较，若该状态更小，就更新f[x][j]
                */
            }
        }
    }
}
int main(){
    //freopen("P4362_6.in","r",stdin);
    cnt=1;
    cin>>n>>m>>K; 
    memset(f,0x3f,sizeof(f));//写0x7f神奇的连样例都过不了
    int fm,to,num;
    for(int i=1;i<=n-1;i++){
        cin>>fm>>to>>num;
        add_edge(fm,to,num);
    }
    if(cnt==K && m>1){
        cout<<-1<<endl;
        return 0;
    }
    dp(1);
    cout<<f[1][K][1]<<endl;
    return 0;
}