链接：http://poj.org/problem?id=1265

Area
Time Limit: 1000MS   Memory Limit: 10000K
Total Submissions: 4969   Accepted: 2231

Description

Being well known for its highly innovative products, Merck would definitely be a good target for industrial espionage. To protect its brand-new research and development facility the company has installed the latest system of surveillance robots patrolling the area. These robots move along the walls of the facility and report suspicious observations to the central security office. The only flaw in the system a competitor抯 agent could find is the fact that the robots radio their movements unencrypted. Not being able to find out more, the agent wants to use that information to calculate the exact size of the area occupied by the new facility. It is public knowledge that all the corners of the building are situated on a rectangular grid and that only straight walls are used. Figure 1 shows the course of a robot around an example area. 

 
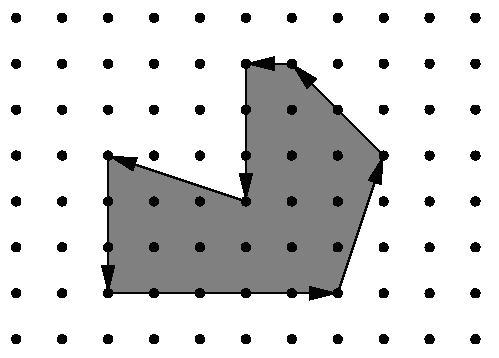
Figure 1: Example area. 

You are hired to write a program that calculates the area occupied by the new facility from the movements of a robot along its walls. You can assume that this area is a polygon with corners on a rectangular grid. However, your boss insists that you use a formula he is so proud to have found somewhere. The formula relates the number I of grid points inside the polygon, the number E of grid points on the edges, and the total area A of the polygon. Unfortunately, you have lost the sheet on which he had written down that simple formula for you, so your first task is to find the formula yourself. 

Input

The first line contains the number of scenarios. 
For each scenario, you are given the number m, 3 <= m < 100, of movements of the robot in the first line. The following m lines contain pairs 揹x dy�of integers, separated by a single blank, satisfying .-100 <= dx, dy <= 100 and (dx, dy) != (0, 0). Such a pair means that the robot moves on to a grid point dx units to the right and dy units upwards on the grid (with respect to the current position). You can assume that the curve along which the robot moves is closed and that it does not intersect or even touch itself except for the start and end points. The robot moves anti-clockwise around the building, so the area to be calculated lies to the left of the curve. It is known in advance that the whole polygon would fit into a square on the grid with a side length of 100 units. 

Output

The output for every scenario begins with a line containing 揝cenario #i:� where i is the number of the scenario starting at 1. Then print a single line containing I, E, and A, the area A rounded to one digit after the decimal point. Separate the three numbers by two single blanks. Terminate the output for the scenario with a blank line.

Sample Input

2
4
1 0
0 1
-1 0
0 -1
7
5 0
1 3
-2 2
-1 0
0 -3
-3 1
0 -3

Sample Output

Scenario #1:
0 4 1.0

Scenario #2:
12 16 19.0

Source

 

-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=

 Pick定理的证明推荐个网址：episte.math.ntu.edu.tw/articles/sm/sm_25_10_1/page2.html

Area=i + b/2 - 1

i为内点 b为边上点

还有点在多边形边上运用GCD的证明，确实不会，希望大神看到给我解释一下

 

 

超时代码：

  1 #include <stdio.h>
  2 #include <math.h>
  3 #include <string.h>
  4 #include <stdlib.h>
  5 #include <iostream>
  6 #include <algorithm>
  7 
  8 #define eps 1e-8
  9 #define MAXX 210
 10 using namespace std;
 11 
 12 typedef struct point
 13 {
 14     double x;
 15     double y;
 16 }point;
 17 typedef struct line
 18 {
 19     point st;
 20     point ed;
 21 }line;
 22 
 23 bool dy(double x,double y)
 24 {
 25     return x>y+eps;
 26 }
 27 bool xy(double x,double y)
 28 {
 29     return x<y-eps;
 30 }
 31 bool dyd(double x,double y)
 32 {
 33     return x>y-eps;
 34 }
 35 bool xyd(double x,double y)
 36 {
 37     return x<y+eps;
 38 }
 39 bool dd(double x,double y)
 40 {
 41     return fabs(x-y)<eps;
 42 }
 43 
 44 double crossProduct(point a,point b,point c)//ac -> ab
 45 {
 46     return (c.x-a.x)*(b.y-a.y)-(c.y-a.y)*(b.x-a.x);
 47 }
 48 double dist(point a,point b)
 49 {
 50     return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
 51 }
 52 
 53 bool onSegment_1(point a,point b,point c)
 54 {
 55     double maxx=max(a.x,b.x);
 56     double minx=min(a.x,b.x);
 57     double maxy=max(a.y,b.y);
 58     double miny=min(a.y,b.y);
 59 
 60     if(dd(crossProduct(a,b,c),0.0) && xyd(c.x,maxx) && dyd(c.x,minx)
 61        && xyd(c.y,maxy) && dyd(c.y,miny))
 62         return true;
 63     return false;
 64 }
 65 
 66 bool segIntersect_1(point p1,point p2,point p3,point p4)
 67 {
 68     double d1=crossProduct(p3,p4,p1);
 69     double d2=crossProduct(p3,p4,p2);
 70     double d3=crossProduct(p1,p2,p3);
 71     double d4=crossProduct(p1,p2,p4);
 72 
 73     if(xy(d1*d2,0.0) && xy(d3*d4,0.0))
 74         return true;
 75     if(dd(d1,0.0) && onSegment_1(p3,p4,p1))
 76         return true;
 77     if(dd(d2,0.0) && onSegment_1(p3,p4,p2))
 78         return true;
 79     if(dd(d3,0.0) && onSegment_1(p1,p2,p3))
 80         return true;
 81     if(dd(d4,0.0) && onSegment_1(p1,p2,p4))
 82         return true;
 83     return false;
 84 }
 85 
 86 point p[MAXX];
 87 line li[MAXX];
 88 int n;
 89 
 90 bool inPolygon_1(point pot)
 91 {
 92     int count=0;
 93     line l;
 94     l.st=pot;
 95     l.ed.x=1e10;
 96     l.ed.y=pot.y;
 97     p[n]=p[0];
 98     for(int i=0; i<n; i++)
 99     {
100         if( onSegment_1(p[i],p[i+1],pot ))
101             return true;
102         if(!dd(p[i].y,p[i+1].y))
103         {
104             int tmp=-1;
105             if(onSegment_1(l.st,l.ed,p[i]))
106                 tmp=i;
107             else if(onSegment_1(l.st,l.ed,p[i+1]))
108                 tmp=i+1;
109             if(tmp != -1 && dd(p[tmp].y,max(p[i].y,p[i+1].y)))
110                 count++;
111             else if(tmp == -1 && segIntersect_1(p[i],p[i+1],l.st,l.ed))
112                 count++;
113         }
114     }
115     if(count % 2 ==1)
116         return true;
117     return false;
118 }
119 
120 bool inPolygon_2(point pot)
121 {
122     int count=0;
123     line l;
124     l.st=pot;
125     l.ed.x=1e10;
126     l.ed.y=pot.y;
127     p[n]=p[0];
128     for(int i=0; i<n; i++)
129     {
130         if( onSegment_1(p[i],p[i+1],pot ))
131             return false;
132         if(!dd(p[i].y,p[i+1].y))
133         {
134             int tmp=-1;
135             if(onSegment_1(l.st,l.ed,p[i]))
136                 tmp=i;
137             else if(onSegment_1(l.st,l.ed,p[i+1]))
138                 tmp=i+1;
139             if(tmp != -1 && dd(p[tmp].y,max(p[i].y,p[i+1].y)))
140                 count++;
141                 else if(tmp == -1 && segIntersect_1(p[i],p[i+1],l.st,l.ed))
142                 count++;
143         }
144     }
145     if(count % 2 ==1)
146         return true;
147     return false;
148 }
149 
150 double Area(int n)
151 {
152     if(n<3)return 0;
153     int i;
154     double ret=0.0;
155     for(i=2; i<=n; i++)
156     {
157         ret+=(crossProduct(p[0],p[i-1],p[i]));
158     }
159     return fabs(ret)/2.0;
160 }
161 
162 int main()
163 {
164     int m,i,j;
165     int ttmp=1;
166     scanf("%d",&m);
167     while(m--)
168     {
169         scanf("%d",&n);
170         p[0].x=0;p[0].y=0;
171         double x,y;
172         double maxx=-100,maxy=-100,minx=100,miny=100;
173         for(i=1; i<=n; i++)
174         {
175             scanf("%lf%lf",&x,&y);
176             p[i].x=p[i-1].x+x;
177             p[i].y=p[i-1].y+y;//printf("%lf %lf^^",p[i].x,p[i].y);
178         }
179         for(i=0; i<=n; i++)
180         {
181             maxx=maxx>p[i].x?maxx:p[i].x;
182             maxy=maxy>p[i].y?maxy:p[i].y;
183             minx=minx<p[i].x?minx:p[i].x;
184             miny=miny<p[i].y?miny:p[i].y;
185         }//printf("%lf %lf^^%lf %lf**",minx,maxx,miny,maxy);
186         int in=0,edge=0,sum=0;
187         point cas;
188         for(i=minx; i<=maxx; i++)
189         {
190             for(j=miny; j<=maxy; j++)
191             {
192                 cas.x=i;cas.y=j;
193                 if(inPolygon_1(cas))
194                 {
195                     sum++;
196                 }
197                 if(inPolygon_2(cas))
198                 {
199                     in++;
200                 }
201             }
202         }
203         double area=Area(n);
204         edge=sum-in;
205         printf("Scenario #%d:\n",ttmp++);
206         printf("%d %d %.1lf\n",in,edge,area);
207     }
208     return 0;
209 }
View Code

 

Pick定理运用

 1 #include <stdio.h>
 2 #include <math.h>
 3 #include <string.h>
 4 #include <stdlib.h>
 5 #include <iostream>
 6 #include <algorithm>
 7 
 8 #define eps 1e-8
 9 #define MAXX 210
10 
11 typedef struct point
12 {
13     double x;
14     double y;
15 }point;
16 
17 int gcd(int a,int b)
18 {
19     return b ? gcd(b,a%b) : a;
20 }
21 
22 double crossProduct(point a,point b,point c)
23 {
24     return (c.x-a.x)*(b.y-a.y)-(c.y-a.y)*(b.x-a.x);
25 }
26 
27 point p[MAXX];
28 int onBorder(int n)
29 {
30     int sum=0;
31     for(int i=0; i<n; i++)
32     {
33         sum+=gcd(abs((int)(p[i].x-p[i+1].x)),abs((int)(p[i].y-p[i+1].y)));
34     }
35     return sum;
36 }
37 
38 double area(int n)
39 {
40     double ans=0.0;
41     for(int i=2; i<=n; i++)
42     {
43         ans+=crossProduct(p[0],p[i-1],p[i]);
44     }
45     return fabs(ans)/2.0;
46 }
47 
48 int main()
49 {
50     int n,m,i,j;
51     scanf("%d",&n);
52     int cas=1;
53     while(n--)
54     {
55         scanf("%d",&m);
56         p[0].x=0;p[0].y=0;
57         double x,y;
58         for(i=1; i<=m; i++)
59         {
60             scanf("%lf%lf",&x,&y);
61             p[i].x=p[i-1].x+x;
62             p[i].y=p[i-1].y+y;
63         }
64         double are=area(m);
65         int edge=onBorder(m);
66         printf("Scenario #%d:\n",cas++);
67         printf("%d %d %.1lf\n\n",(int)are+1-edge/2,edge,are);
68     }
69     return 0;
70 }
View Code