http://poj.org/problem?id=2653
Pick-up sticks
| Time Limit: 3000MS | Memory Limit: 65536K | |
| Total Submissions: 9531 | Accepted: 3517 |
Description
Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.
Input
Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.
Output
For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.
The picture to the right below illustrates the first case from input.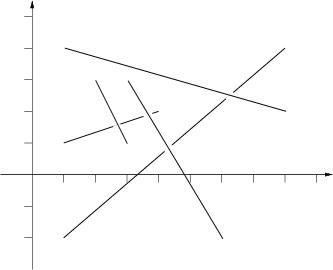
The picture to the right below illustrates the first case from input.

Sample Input
5 1 1 4 2 2 3 3 1 1 -2.0 8 4 1 4 8 2 3 3 6 -2.0 3 0 0 1 1 1 0 2 1 2 0 3 1 0
Sample Output
Top sticks: 2, 4, 5. Top sticks: 1, 2, 3.
Hint
Huge input,scanf is recommended.
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
-------------------------------------------------------------------------
注意当判断出当前线已经被挡住后,要跳出循环,否者会超时

#include <stdio.h> #include <string.h> #include <stdlib.h> #include <iostream> #include <stdlib.h> #include <math.h> #include <algorithm> using namespace std; #define MAXX 100010 #define eps 1e-6 typedef struct point { double x,y; }point; typedef struct { point st,ed; }line; bool xy(double x,double y){ return x<y-eps; } bool dy(double x,double y){ return x>y+eps; } bool xyd(double x,double y){ return x<y+eps; } bool dyd(double x,double y){ return x>y-eps; } bool dd(double x,double y){ return fabs(x-y)<eps; } double crossProduct(point a,point b,point c) { return (c.x-a.x)*(b.y-a.y)-(c.y-a.y)*(b.x-a.x); } bool onSegment(point a,point b,point c) { double maxx=max(a.x,b.x); double maxy=max(a.y,b.y); double minx=min(a.x,b.x); double miny=min(a.y,b.y); if(dd(crossProduct(a,b,c),0.0)&&dyd(c.x,minx) &&xyd(c.x,maxx)&&dyd(c.y,miny)&&xyd(c.y,maxy)) return true; return false; } bool segIntersect(point p1,point p2,point p3,point p4) { double d1=crossProduct(p3,p4,p1); double d2=crossProduct(p3,p4,p2); double d3=crossProduct(p1,p2,p3); double d4=crossProduct(p1,p2,p4); if(xy(d1*d2,0.0)&&xy(d3*d4,0.0)) return true; if(dd(d1,0.0)&&onSegment(p3,p4,p1)) return true; if(dd(d2,0.0)&&onSegment(p3,p4,p2)) return true; if(dd(d3,0.0)&&onSegment(p1,p2,p3)) return true; if(dd(d4,0.0)&&onSegment(p1,p2,p4)) return true; return false; } point p[MAXX]; line li[MAXX]; int num[MAXX]; int main() { int m,n,i,j; while(scanf("%d",&n)!=EOF&&n) { memset(num,0,sizeof(num)); for(i=0;i<n;i++) { scanf("%lf%lf%lf%lf",&li[i].st.x,&li[i].st.y,&li[i].ed.x,&li[i].ed.y); } for(i=0;i<n;i++) { for(j=i+1;j<n;j++) { if(segIntersect(li[i].st,li[i].ed,li[j].st,li[j].ed)) { num[i]++; break; } } } int cas=0,tes=0,tmp; //int str[MAXX]; for(i=0;i<n;i++) { if(num[i] == 0) { cas++; } } printf("Top sticks: "); for(i=0;i<n;i++) { if(num[i] == 0 && tes<cas-1) { printf("%d, ",i+1); tes++; tmp=i; } }//printf("%d**",i); for(j=tmp+1;j<n;j++) { if(num[j] == 0) { printf("%d.\n",j+1); } } } return 0; }



