剑指offer解题思路锦集1-10题

1、【二维有序数组查找】

 

在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

 

方案肯定是要用O(n)级别的，如果是O(N^2)，那么还就是暴力破解。这样根本就没有利用到题目的性质====》二维有序数组，所以还是老老实实想O(N)的算法吧！

 

即存在数组满足以下规律：

	 ------>
	|
	|
	|
	↓
问怎么如何快速找到其中的一个元素？

 

 

存在问题：问题来了，如果从(0,0)出发，那么问题肯定是极度恶心的，因为根本不知道下一次是往下走还是往右边走。。。因为【两个方向都是增加的】

发现问题：这时候我们得知了问题点在于【从(0,0)出发，会使得无论往右还是往下都是增加。】那么是否存在某个点使得【一个方向增加一个方向减少】？
解决问题：使用(0,n-1)点或者(n-1,0)点，会发现一个方向是增加，一个方向是减少。如果值小了，那么就往增加方向查找，如果值大了，就往减少方向减少。这时候代码就十分的轻而易举写出来了。

 

代码：

 

    bool Find(int target, vector<vector<int> > array) {
        int row = array.size();
        int col = array[0].size();
        for (int i = 0,j = col - 1; i < row && j >= 0;)
        {
            if (array[i][j] == target)
            {
                return true;
            }
            if (array[i][j] < target)
            {
                ++i;
            }
            else 
            {
                --j;
            }
        }
        return false;
    }

 

 

 

2、【替换空格】

 

题目：请实现一个函数，将一个字符串中的空格替换成“%20”。例如，当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。

前提：传入的空间是长度足够大的。不然这题就没有啥意义了，简单的计算要申请多少内存，然后申请好了内存，从左到右慢慢拷贝就行了，时间复杂度和空间复杂度都是O(n)。
只有在传入的空间是足够大时候，才可以考虑能不能在O(1)空间复杂度和O(n)时间复杂度时候完成这个事情。

思路：从头开始拷贝也是巨复杂无比的，因为根本不知道拷贝去哪里，会不会覆盖了本身的字符串。。。
问题根源：在于选择了一个错误的方向，这时候我们可以想想能不能从后往前拷贝呢？？？如果可以，这样思路就变得很简单了。。。

代码：

    int getSpaceNum(char *str){
        int spaceNum = 0;
        if (NULL == str)
        {
            return spaceNum;
        }

        while(*str++ != '\0')
        {
            ++spaceNum;
        }
        return spaceNum;

    }
    void replaceSpace(char *str,int length) {
        int spaceNum = getSpaceNum(str);
        int end = length + spaceNum * 2;
        if end
        while(--length > 0)
        {
            char ch = str[length];
            if (ch == ' ')
            {
                str[--end] = '0';
                str[--end] = '2';
                str[--end] = '%';
            }
            else
            {
                str[--end] = ch;
            }
        }

    }

 

 

3、【从尾到头打印链表】

 

题目：输入一个链表，从尾到头打印链表每个节点的值。

思路：啥也不用想了，，简单的一个尾递归就OK了。

 

问题：从尾到头打印单链表(1,2,3,4,5...n)

分解成：从尾到头打印单链表(2,3,4,5...n) 问题+ 打印值1

简单的分治想法，就完成了。。。

 

代码

    void printListFromTailToHead(ListNode* head, vector<int> &vec)
    {
        if(head == NULL) return;
        printListFromTailToHead(head->next, vec);
        vec.push_back(head->val);
    }
    vector<int> printListFromTailToHead(ListNode* head) {
    	vector<int> vec;
        printListFromTailToHead(head, vec);
        return vec;
    }

 

4、【重建二叉树】

 

题目：输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

思路：还是使用分治思路啊，老铁。

假设输入为：前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}。

首先得到头结点1，左子树中序遍历序列{4,7,2}，右子树中序遍历序列{5,3,8,6}

      再得到左子树前序遍历序列{,2,4,7}，右子树中序遍历序列{3,5,6,8}。

接下来不就是分治了么？？？

 

代码：

　　TreeNode* reConstructBinaryTree(vector<int> pre, int preStart, int preEnd, vector<int> vin, int vinStart, int vinEnd) {
        if (preStart > preEnd || vinStart > vinEnd)
        {
            return NULL;
        }
        int value = pre[preStart];
        TreeNode *root = new TreeNode(value);
        for (int i = vinStart; i <= vinEnd; ++i)
        {
            if (value == vin[i])
            {
                int leftTreeSize = i - vinStart;
                root->left = reConstructBinaryTree(pre, preStart+1, preStart + leftTreeSize, vin, vinStart, i - 1);
                root->right = reConstructBinaryTree(pre, preStart + leftTreeSize + 1, preEnd, vin, i + 1, vinEnd);
            }
        }
        return root;
    }

    TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {
        int preSize = pre.size();
        int vinSize = vin.size();
        if (preSize == 0 || preSize != vinSize)
        {
            return NULL;
        }
        return reConstructBinaryTree(pre, 0, preSize - 1, vin, 0, vinSize - 1);
    }

 

5、【用两个栈来实现一个队列】

 

题目：用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

思路：

　　假设存在两个栈stack1、stack2，可以这样认为：

　　　　stack2中保存的为【队列的前部分元素】，可以认为 其栈顶值 = 队列头部值。

　　　　stack1中的元素为【未经转换的队列后部分元素】，相当于buffer一样的存在，它其实就是队列中后部分元素逆序的结果。因此需要将其元素全部投入到stack2中，这样完成翻转过程。

 

画图如下：

|  <----      队列        ----> | |  <- 栈2 ->   |  <- 栈1 ->     | | 和队列顺序一致 |  和队列顺序相反  |

 

代码如下：

class Solution
{
public:
    void push(int node) {
        stack1.push(node);
    }
 
    int pop() {
        if (stack2.size() == 0)
        {
            while ( !stack1.empty())
            {
                stack2.push(stack1.top());
                stack1.pop();
            }
        }
        int value = stack2.top();
        stack2.pop();
        return value;
    }
 
private:
    stack<int> stack1;
    stack<int> stack2;
};

 

6、【旋转数组的最小元素】

题目：把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

 

其实这条题类似二分查找一样，二分查找分析的是中点和左节点，或者分析中点和右节点。而这里也是类似的，要么分析【中点和左节点】，或者【分析中点和右节点】。

我们为了简单，就分析中点和左节点。。。

先画图如下：

思考过程：
1、如果发现arr[mid] >= arr[start]，那么说明了[start, mid]处于非递减状态，也就是说断点不可能出现在这里。因此这时候可以搜索[mid, end]
2、如果发现arr[mid] < arr[start]，那么说明了啥？[start,mid]之间就存在着断点！

有没有什么要注意的点呢？有的！那就是可能存在直线状态，这时候发现了arr[start] == arr[end]，这时候只能直线搜索了。。。

 

代码：

    int FidMin(vector<int> &arr,int start,int end)
    {
        int res = arr[start];
        for(int i = start+1;i<=end;++i)
        {
            if(arr[i]>res)res=arr[i];
        }
        return res;
    }
    int minNumberInRotateArray(vector<int> rotateArray) {
        int n = rotateArray.size();
        if(n <= 0) return 0;
       // if(n == 1) return rotateArray[0];
        //下 上
   		int start = 0;
        int end = n-1;
        int mid = (start+end)/2;
        while(rotateArray[start] >= rotateArray[end])
        {
            if(end-start<=1){mid = end;break;}
            mid = (start+end)/2;
            if(rotateArray[start] == rotateArray[end]&&rotateArray[end] == rotateArray[mid])//一条直线
                return FidMin(rotateArray,start,end);
            if(rotateArray[mid] >= rotateArray[start]){start = mid;}
          //  else if(rotateArray[mid] > rotateArray[end]){end = mid;}///////只能else???
            else {end = mid;}
        }
        return rotateArray[mid];
    }

 

7、【斐波那契数列】

题目：大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项。

这是一条很有意思的题目，有的人看到了就直接脑袋一拍，这不是可以用递归吗？

return n < 2? 1: fib(n-1) + fib(n-2);

不考虑时间复杂度和空间复杂度时候，这是一个解，但是却是一个很糟糕的解，因为其空间复杂度和时间复杂度都很高，接近O(2ⁿ) ，准确来说是O(((1+根号5)/2)ⁿ)。

 

那么怎么优化呢？最简单的优化思路是，发现到其中存在大量的计算都是重复的，很多计算都是多余的递归，那么我们可不可以搞一个带记忆版本的递归呢？对于已经计算过的斐波那契数列，就不用再算，嗯，大概就是这个意思。。。

根据这个想法不难得到代码如下：

#!/usr/bin/env python
# coding=utf-8

def _fib(n, buff):
    if buff[n] != -1:
        return buff[n]

    buff[n] = _fib(n-1, buff) + _fib(n-2, buff)
    return buff[n]

def fib(n):
    if n <= 0:
        return 0
    if n < 2:
        return 1

    # 初始化
    buff = (n + 1) * [-1]
    buff[0] = 0
    buff[1] = 1
    buff[2] = 1
    return _fib(n, buff)

print fib(1)
print fib(2)
print fib(3)
print fib(4)
print fib(5)
print fib(6)
print fib(7)

 

但是这种解决方案是丑陋的，因为其还是用到了递归，那么我们能不能尝试不用递归呢？我们想到了数学归纳法，也就是所谓的动态规划。它和递归差别在于递归想法是自顶向下，而动态规划是自下往上。

思路如下：

假设我们已知fib(n-1)和fib(n-2)的值，那么下一个值就为fib(n-1)+fib(n-2)。是不是很简单？没错，这东西就好像数学归纳法一样。。。

 

代码如下：

#!/usr/bin/env python
# coding=utf-8

def fib(n):
    if n <= 0:
        return 0
    if n < 2:
        return 1

    # 初始化
    buff = (n + 1) * [-1]
    buff[0] = 0
    buff[1] = 1
    buff[2] = 1
    for i in range(2, n + 1):
        buff[i] = buff[i-1] + buff[i-2]
    return buff[n]

print fib(1)
print fib(2)
print fib(3)
print fib(4)
print fib(5)
print fib(6)
print fib(7)

 

再仔细考虑下代码是否还能继续优化？无疑是存在，因为我们从代码中发现了：每次执行循环都是使用了buff[i-1]和buff[i-2]两个变量。但是其他buff[0:i-1]全部没用。这样我们是不是可以思考：是否不用这个数组，用两个变量来保存？答案是可以的。这就是每一本C语言书上介绍的循环版本的非递归斐波那契计算方法。

def fib(n):
    if n <= 0:
        return 0
    if n < 2:
        return 1

    # 初始化
    f = 1
    f1 = 1
    f2 = 1
    for i in range(2, n):
        f = f1 + f2
        f2 = f1 # 更新下一次的buff[n-2]
        f1 = f  # 更新下一次的buff[n-1]

    return f

print fib(1)
print fib(2)
print fib(3)
print fib(4)
print fib(5)
print fib(6)
print fib(7)

 

还能优化吗？？？？？？？这里留下了一个深深的疑问？是否有比O(n)更优的算法？？必然是存在的。。。就是大名鼎鼎的代入公式就可以了。

高中数学，，，计算特征根方程，，不过这里涉及到数学。。。就不怎么说了，简单贴上一个链接吧：

　　  求数列通项的特征根法  http://www.360doc.com/content/16/0117/10/2289804_528556906.shtml

我们只取其结果就可以了。

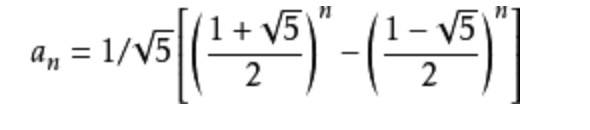
这时候我们直接调数学函数就可以了，不用递归，也不用循环，哈哈。但是是存在问题的，就是如何利用O(lg n)时间复杂度去计算Xⁿ？先看后面章节有没有讲到吧，如果没有的话，那么我再补充一下。。。反正知道这个只要O(lg n)就可以了。。

 

8、【跳台阶】

题目：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。 

 

这个题是用分治想法来解的，首先青蛙在第一次跳时候，可以跳1步或者2步。

　　假设跳1步，那么问题就变成了“青蛙跳n-1个台阶一共有多少种方法”，

　　假设跳2步，那么问题就变成了"青蛙跳n-2个台阶一共有多少种方法"。

所以啊，青蛙可以跳一步或两步，也就是说，问题是由 “青蛙跳n-1个台阶一共有多少种方法” 或 “青蛙跳n-2个台阶一共有多少种方法” 两个选项。也就是 fun(n-1)+fun(n-2)。斐波那契数列。。。

 

代码就不给了额，，，

 

9、【变态跳台阶】

问题：一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

 

n = 1 return 1
n = 2 return 2
n > 2 return a^n-1 + a^n-2 +...+ a² + a¹

也就是说  aⁿ = a^n-1 + a^n-2 +...+ a² + a¹

又因为 a^n-1 = a^n-2 +a^n-3...+ a² + a¹

所以有aⁿ = a^n-1 +(a^n-2 +...+ a² + a¹) =  a^n-1+a^n-1=2a^n-1

所以懂了吧，简单一句return 1<< --n就是答案啦~~~

 

代码如下：

    int jumpFloorII(int number) {
		return 1<<--number;
    }

 

10、【矩形覆盖】

问题：我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

 

这题基本和青蛙跳台阶一模一样的分析过程。。。

 

这个题也是用分治想法来解的，首先在第一次覆盖时候，可以横着覆盖或者竖着覆盖。

　　假设横着覆盖，那么问题就变成了“覆盖2*(n-2)的矩阵一共有多少种方法”，

　　假设竖着覆盖，那么问题就变成了"覆盖2*(n-1)的矩阵一共有多少种方法"。

所以啊，横着覆盖或者竖着覆盖，也就是说，问题是由 “覆盖2*(n-2)的矩阵一共有多少种方法” 或 “覆盖2*(n-1)的矩阵一共有多少种方法” 两个选项。也就是 fun(n-1)+fun(n-2)。斐波那契数列。。。

 

代码也就不写了哈。