《视觉SLAM十四讲》笔记(ch8)
ch8-视觉里程计2
主要目标:1.理解光流法跟踪特征点的原理
2.理解直接法是如何估计相机位姿的
3.使用g2o进行直接法的计算
本讲我们将介绍直接法的原理,并利用g2o实现直接法中的一些核心算法。
特征点法的缺点:
1)关键点的提取与描述子的计算非常耗时。SIFT无法在CPU上实时计算,而即使是相对较快的ORB也要将近20ms的计算。对于30ms/帧运行的SLAM系统来说,一大半时间都花在了计算特征点上。
2)使用特征点时,忽略了除特征点以外的所有信息。一副图像有几十万个像素,而特征点只有几百个。只使用特征点丢失了大部分可能有用的图像信息。
3)如果相机运动到特征缺失的地方,比如说一堵白墙,或者一个空荡荡的走廊,这些地方往往没有明显的纹理信息。从而特征点数量也会明显减少,以至于我们可能就找不到足够的匹配点来计算相机的运动。
相应的解决方法:
1)保留特征点,但只计算关键点,不计算描述子。同时,使用光流法(Optical Flow)来跟踪特征点的运动。这样可回避计算和匹配描述子带来的时间,但是光流本身也需要一定时间。(这种方法仍然使用特征点,只是把匹配描述子替换成了光流跟踪,估计相机运动时仍然使用对极几何、PnP或ICP算法。)实践见下。
(接下来的两种算法,是根据图像的像素灰度信息来计算相机运动,称之为直接法)
2)只计算关键点,不计算描述子。同时,使用直接法(Direct Method)来计算特征点在下一时刻图像中的位置。这样也能跳过描述子的计算过程,并且直接法的计算更加简单。(稀疏直接法)
3)既不计算关键点,也不计算描述子,而是根据像素灰度值的差异,直接计算相机运动。(半稠密 and 稠密)
特征点法 VS 直接法
1)特征点法计算量较大(计算描述子)
2)仅提取图像上的特征点会浪费了图像上大部分可能有用的信息(一副图像有几十万个像素,而特征点只有几百个)
3)对于特征缺失的场景,特征点法失效
4)在应用场合上的限定:特征点法只能重构稀疏特征点(稀疏地图),而直接法可以恢复半稠密或甚至是稠密的地图。
5)SLAM求解优化过程中主要优化点的特征和位置匹配代价:在特征法中点的特征匹配由特征描述子确定,求解只优化点特征匹配状态下的位置代价;直接法则是对点的特征(灰度)和位置同时进行优化,是更加end2end的方法,其优势在于避免了绝对特征匹配带来的局部最优问题,同时也省去了特征描述的开销。
6)求解方法不同:
用特征点法估计相机运动时,把特征点看作固定在三维空间的不动点。根据这些特征点在相机中的投影位置,通过最小化重投影误差(Reprojection error)(因为通过匹配描述子知道了空间点在两个相机中投影后的像素位置,所以可以计算重投影的位置)来优化相机运动。因为在这个过程中,我们需要精确的知道空间点在两个相机中投影后的像素位置,所以就要对匹配或跟踪特征。而计算、匹配特征需要付出大量的计算量。
在直接法中,我们并不知道点与点之间的对应关系(第二个相机中的哪一个投影点对应第一个相机中的投影点,直接法的思路是根据当前相机的位姿估计值来寻找第二个i相机中的投影点的位置),而是通过最小化光度误差(Photometric error)来求得它们。
相对于特征点法,直接法的优点:
首先要知道直接法的存在就是为了克服特征点法的缺点。1)直接法根据像素的亮度信息估计相机的运动,故而可以完全不用计算关键点和描述子。这样,既避免了特征点的计算时间,又避免了特征缺失的情况。2)特征点法只能重构稀疏特征点(稀疏地图),而直接法还可以恢复稠密或半稠密结构的地图。
使用直接法的场景要求:场景中要存在明暗变化(可以是渐变,不形成局部的图像梯度)
直接法的分类:根据使用像素的数量,分为稀疏、稠密、半稠密
直接法是从光流演变而来,两者非常相似,具有相同的假设条件。为了说明直接法,先来介绍光流。
1.光流(Optical FLow)
是一种描述像素随时间在图像之间运动的方法。
分类:1)稀疏光流——计算部分像素的运动,代表:Lucas-Kanade(LK)光流:通常被用来跟踪角点的运动
灰度不变假设:同一个空间点的像素灰度值,在各个图像中是固定不变的。(这是一个很强的假设,实际当中很可能不成立)
2)稠密光流——计算所有像素的运动
1.1 实践:LK光流
演示如何使用OpenCV提供的光流法来跟踪特征点:在实际应用中,LK光流的作用就是跟踪特征点。与对每一帧提取特征点相比,使用LK光流只需要提取一次特征点,后续视频帧只需要跟踪就可以了,节约了许多特征提取时间。首先对第一幅图像提取FAST角点,然后用LK光流跟踪它们,并画在图中。
代码如下:
1 #include <iostream> 2 #include <fstream> 3 #include <list> 4 #include <vector> 5 #include <chrono> 6 #include <opencv2/core/core.hpp> 7 #include <opencv2/highgui/highgui.hpp> 8 #include <opencv2/features2d/features2d.hpp> 9 #include <opencv2/video/tracking.hpp>//LK Flow 10 11 using namespace std; 12 13 int main(int argc,char** argv) 14 { 15 if(argc!=2) 16 { 17 cout<<"usage:useLK path_to_dataset"<<endl; 18 return 1; 19 } 20 21 string path_to_dataset=argv[1]; 22 //associate.txt:根据rgb和depth两个文件的采集时间进行配对得到的 23 string associate_file=path_to_dataset+"/associate.txt"; 24 // cout<<associate_file<<endl; 25 ifstream fin(associate_file);//利用ifstream类的构造函数创建一个文件输入流对象 26 if(!fin) 27 { 28 cerr<<"I cann't find associate.txt!"<<endl; 29 return 1; 30 } 31 32 string rgb_file,depth_file,time_rgb,time_depth; 33 list<cv::Point2f> keypoints;//因为要删除跟踪失败的点,使用list 34 cv::Mat color,depth,last_color; 35 36 37 for(int index=0;index<100;++index) 38 { 39 fin>>time_rgb>>rgb_file>>time_depth>>depth_file;//从文件associate.txt中读数据 40 // cout<<time_rgb<<" "<<rgb_file<<" "<<time_depth<<" "<<depth_file; 41 color=cv::imread(path_to_dataset+"/"+rgb_file); 42 depth=cv::imread(path_to_dataset+"/"+depth_file,-1); 43 // cv::imshow("color.png",color); 44 // cv::imshow("depth.png",depth); 45 if(index==0) 46 { 47 //对第一帧提取FAST特征点 48 //只对第一个图像提取特征。然后对第一幅图像提取的特征进行追踪。 49 vector<cv::KeyPoint> kps; 50 cv::Ptr<cv::FastFeatureDetector> detector=cv::FastFeatureDetector::create(); 51 //检测FAST角点位置 52 detector->detect(color,kps); 53 for(auto kp:kps) 54 keypoints.push_back(kp.pt); 55 last_color=color; 56 continue; 57 } 58 if(color.data==nullptr||depth.data==nullptr) 59 continue; 60 //对其他帧用LK跟踪特征点 61 vector<cv::Point2f> next_keypoints; 62 vector<cv::Point2f> prev_keypoints; 63 for(auto kp:keypoints) 64 prev_keypoints.push_back(kp); 65 vector<unsigned char> status; 66 vector<float> error; 67 chrono::steady_clock::time_point t1=chrono::steady_clock::now(); 68 cv::calcOpticalFlowPyrLK(last_color,color,prev_keypoints,next_keypoints,status,error);//可得到新一帧中更新后的特征点位置 69 70 chrono::steady_clock::time_point t2=chrono::steady_clock::now(); 71 chrono::duration<double> time_used=chrono::duration_cast<chrono::duration<double>>(t2-t1); 72 cout<<"LK Flow use time: "<<time_used.count()<<" seconds."<<endl; 73 //把跟丢的点删掉 74 int i=0; 75 for(auto iter=keypoints.begin();iter!=keypoints.end();++i) 76 { 77 //status? 78 if(status[i]==0)//说明跟丢了 79 { 80 iter=keypoints.erase(iter); 81 continue; 82 } 83 *iter=next_keypoints[i]; 84 ++iter; 85 } 86 cout<<"tracked keypoints: "<<keypoints.size()<<endl; 87 if(keypoints.size()==0) 88 { 89 cout<<"all keypoints are lost."<<endl; 90 break; 91 } 92 //画出keypoints 93 cv::Mat img_show=color.clone(); 94 for(auto kp:keypoints) 95 cv::circle(img_show,kp,10,cv::Scalar(0,240,0),1); 96 cv::imshow("corners",img_show); 97 cv::waitKey(0); 98 last_color=color; 99 } 100 return 0; 101 }
运行结果:
各帧特征点提取情况:



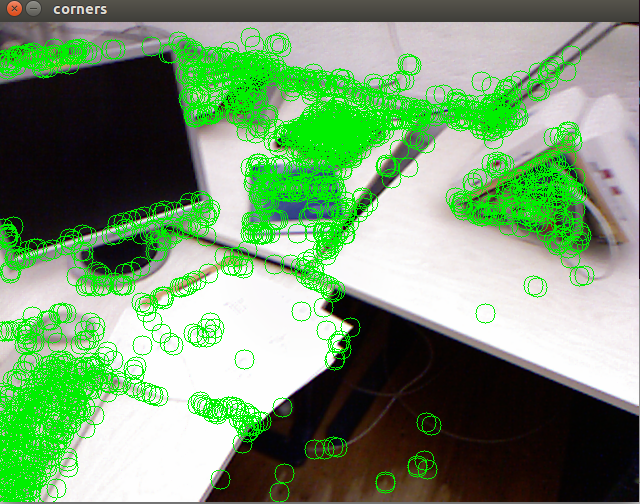



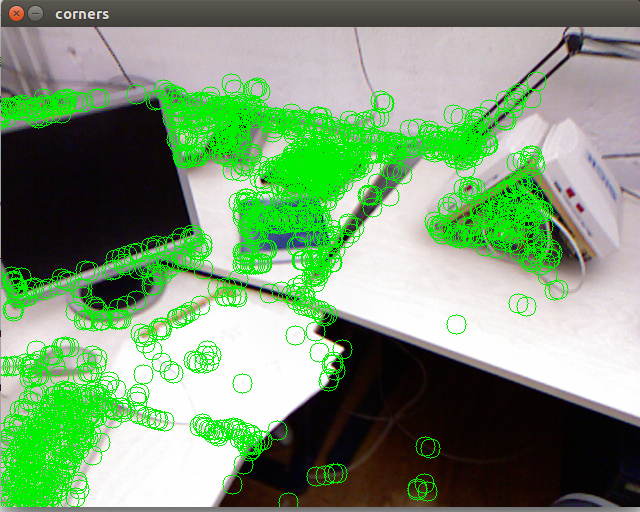
观察特征点的跟踪过程,我们发现1)位于物体角点处的特征更加稳定。2)边缘处的特征会沿着边缘“滑动”,主要是因为沿着边缘移动时特征块的内容基本不变,因此程序容易认为是同一个地方。3)既不在角点也不在边缘的特征点则会频繁跳动,位置非常不稳定。“金角银边草肚皮”:角点具有更好的辨识度,边缘次之,区块最少。
在本例中,LK跟踪法避免了描述子的计算与匹配,但本身也需要一定的计算量。在具体的SLAM系统中,使用光流还是匹配描述子,最好自己做实验测试。
LK光流跟踪能够直接得到特征点的对应关系,这个对应关系就像是描述子的匹配。
光流相对于描述子的优势:在光流法中,,大多数时候只会碰到特征点跟丢的情况,而不太会遇到误匹配。
缺点:匹配描述子的方法在相机运动较大时仍能成功,而光流法要求相机的运动必须是微小的。所以,光流的健壮性要差于描述子。
总结:光流法可加速基于特征点的视觉里程计算法,避免计算和匹配描述子的过程,但要求相机运动较慢(或采集频率较高)。
2.直接法(Direct Method)
先介绍直接法的原理,然后使用g2o实现直接法。
推导直接法估计相机位姿的整个流程见P192-195。
根据一个已知位置的空间点P的来源,对直接法进行分类:
1)稀疏直接法——P来源于稀疏关键点。这种方法不必计算描述子,并且只使用数百个像素,因此速度最快,但只能计算稀疏的重构。
2)半稠密(Semi-Dense)直接法——P来源于部分像素:只使用带有梯度的像素点,舍弃像素梯度不明显的地方,因为如果像素梯度为零,整项雅可比矩阵就为零,不会对计算运动增量有任何贡献(理论依据见P195式(8.16))。可重构一个半稠密结构。
3)稠密直接法——P为所有像素。稠密重构要计算所有像素,所以多数需要GPU的加速。对于像素梯度不明显的点,在运动估计中的贡献不大,在重构的时候也会难以估计位置。
总结:从1)->3)计算量逐渐增加。稀疏法可快速求解相机位姿,适应于实时性较高且计算资源有限的场合。稠密法可建立完整地图。而具体应该使用哪种方法,应该视机器人的应用环境而定。
2.1实践:RGB-D的直接法
2.1.1稀疏直接法(求解直接法=求解一个优化问图:使用g2o优化库)
先定义一种用于直接法位姿估计的边,然后使用该边构建图优化问题并求解。
代码:参考:https://www.cnblogs.com/newneul/p/8571653.html
1 #include <iostream> 2 #include <fstream> 3 #include <list> 4 #include <vector> 5 #include <chrono> 6 #include <ctime> 7 #include <climits> 8 9 #include <opencv2/core/core.hpp> 10 #include <opencv2/imgproc/imgproc.hpp> 11 #include <opencv2/highgui/highgui.hpp> 12 #include <opencv2/features2d/features2d.hpp> 13 //#include <Eigen/Core> 14 //#include <Eigen/Geometry>//Eigen::Isometry3d 15 16 17 #include <g2o/core/base_unary_edge.h> 18 #include <g2o/core/block_solver.h> 19 #include <g2o/core/optimization_algorithm_levenberg.h> 20 #include <g2o/solvers/dense/linear_solver_dense.h> 21 #include <g2o/core/robust_kernel.h> 22 #include <g2o/types/sba/types_six_dof_expmap.h> 23 24 using namespace std; 25 using namespace g2o; 26 using namespace cv; 27 //演示RGBD上的稀疏直接法 28 29 //一次测量的值,包括一个世界坐标系下三维点与一个灰度值 30 struct Measurement 31 { 32 Measurement(Eigen::Vector3d p,float g):pos_world(p),grayscale(g){} 33 Eigen::Vector3d pos_world; 34 float grayscale; 35 }; 36 37 38 inline Eigen::Vector3d project2Dto3D(int x,int y,int d,float fx,float fy,float cx,float cy,float scale) 39 { 40 float zz=float(d)/scale; 41 float xx=zz*(x-cx)/fx; 42 float yy=zz*(y-cy)/fy; 43 return Eigen::Vector3d(xx,yy,zz); 44 } 45 46 47 inline Eigen::Vector2d project3Dto2D ( float x, float y, float z, float fx, float fy, float cx, float cy ) 48 { 49 float u = fx*x/z+cx; 50 float v = fy*y/z+cy; 51 return Eigen::Vector2d ( u,v ); 52 } 53 54 //直接法估计位姿 55 //输入:测量值(空间点的灰度),新的灰度图,相机内参;输出:相机位姿 56 //返回:true,成功;false,失败 57 bool poseEstimationDirect(const vector<Measurement>& measurements,Mat* gray,Eigen::Matrix3f& intrinsics,Eigen::Isometry3d& Tcw); 58 59 60 //由于g2o中本身没有计算光度误差的边,我们需要自己定义一种新的边 61 class EdgeSE3ProjectDirect:public BaseUnaryEdge<1,double,VertexSE3Expmap> 62 { 63 public: 64 EIGEN_MAKE_ALIGNED_OPERATOR_NEW 65 66 EdgeSE3ProjectDirect(){} 67 68 EdgeSE3ProjectDirect ( Eigen::Vector3d point, float fx, float fy, float cx, float cy, cv::Mat* image ) 69 : x_world_ ( point ), fx_ ( fx ), fy_ ( fy ), cx_ ( cx ), cy_ ( cy ), image_ ( image )//灰度图像指针 70 {} 71 72 virtual void computeError() 73 { 74 const VertexSE3Expmap* v=static_cast<const VertexSE3Expmap*> (_vertices[0]); 75 Eigen::Vector3d x_local=v->estimate().map(x_world_); 76 float x=x_local[0]*fx_/x_local[2]+cx_;//u 77 float y=x_local[1]*fy_/x_local[2]+cy_;//v 78 //check x,y is in the image 79 //距离图像四条边4个像素大小的区域内作为有效投影区域,对于不在该范围内的点误差值设为0, 80 //为了防止计算的误差太大,拉低内点对误差的影响,导致估计的R,t严重偏离真值 81 if(x-4<0 || (x+4)>image_->cols || (y-4)<0 || (y+4)>image_->rows) 82 { 83 _error(0,0)=0.0; 84 this->setLevel(1); 85 } 86 else 87 { 88 _error(0,0)=getPixelValue(x,y)-_measurement;//经过在灰度图中插值获取得的像素值减去测量值 89 } 90 } 91 92 //plus in manifold 93 virtual void linearizeOplus() 94 { 95 if(level()==1) 96 { 97 _jacobianOplusXi=Eigen::Matrix<double,1,6>::Zero(); 98 return; 99 } 100 VertexSE3Expmap* vtx=static_cast<VertexSE3Expmap*> (_vertices[0]); 101 Eigen::Vector3d xyz_trans=vtx->estimate().map(x_world_); 102 103 double x=xyz_trans[0]; 104 double y=xyz_trans[1]; 105 double invz=1.0/xyz_trans[2]; 106 double invz_2=invz*invz; 107 108 float u=x*fx_*invz+cx_; 109 float v=y*fy_*invz+cy_; 110 111 //jacobin from se3 to u,v 112 //NOTE that in g2o the Lie alfebra is 113 Eigen::Matrix<double,2,6> jacobian_uv_ksai; 114 115 jacobian_uv_ksai(0,0)=-x*y*invz_2*fx_; 116 jacobian_uv_ksai(0,1)=(1+(x*x*invz_2))*fx_; 117 jacobian_uv_ksai(0,2)=-y*fx_*invz; 118 jacobian_uv_ksai(0,3)=invz*fx_; 119 jacobian_uv_ksai(0,4)=0; 120 jacobian_uv_ksai(0,5)=-x*fx_*invz_2; 121 122 jacobian_uv_ksai(1,0)=-(1+(y*y*invz_2))*fy_; 123 jacobian_uv_ksai(1,1)=x*y*invz_2*fy_; 124 jacobian_uv_ksai(1,2)=x*invz*fy_; 125 jacobian_uv_ksai(1,3)=0; 126 jacobian_uv_ksai(1,4)=invz*fy_; 127 jacobian_uv_ksai(1,5)=-y*invz_2*fy_; 128 129 Eigen::Matrix<double,1,2> jacobian_pixel_uv; 130 131 //书上I2对像素坐标系的偏导数 这里很有可能 计算出来的梯度为0 因为FAST角点的梯度没有限制 132 //这也是半稠密法主要改进的地方 就是选关键点的时候 选择梯度大的点 因此这里的梯度就不可能为0了 133 jacobian_pixel_uv(0,0)=(getPixelValue(u+1,v)-getPixelValue(u-1,v))/2; 134 jacobian_pixel_uv(0,1)=(getPixelValue(u,v+1)-getPixelValue(u,v-1))/2; 135 136 _jacobianOplusXi=jacobian_pixel_uv*jacobian_uv_ksai; 137 } 138 139 //dummy read and write functions because we don't care 140 virtual bool read(std::istream& in){} 141 virtual bool write(std::ostream& out) const{} 142 143 protected: 144 //get a gray scale value from reference image(billinear interpolated) 145 //下面的方式:针对但通道灰度图 146 inline float getPixelValue(float x,float y)//通过双线性插值获取浮点坐标对应的插值后的像素值 147 { 148 uchar* data=& image_->data[int(y)*image_->step+int(x)]; 149 float xx=x-floor(x); 150 float yy=y-floor(y); 151 return float(//公式f(i+u,j+v)=(1-u)(1-v)f(i,j)+u(1-v)f(i+1,j)+(1-u)vf(i,j+1)+uvf(i+1,j+1) 152 //这里的xx就是u,yy就是v 153 (1-xx)*(1-yy)*data[0]+ 154 xx*(1-yy)*data[1]+ 155 (1-xx)*yy*data[image_->step]+ 156 xx*yy*data[image_->step+1] 157 ); 158 } 159 public: 160 Eigen::Vector3d x_world_;//3D point in world frame 161 float cx_=0,cy_=0,fx_=0,fy_=0;//Camera insics 162 Mat* image_=nullptr;//reference image 163 }; 164 165 int main(int argc,char** argv) 166 { 167 if(argc!=2) 168 { 169 cout<<"usage:direct_sparse path_to_dataset"<<endl; 170 return 1; 171 } 172 srand((unsigned int) time(0));//根据时间生成一个随机数 173 //srand目的就是让得到的序列看上去更贴近随机的概念 174 string path_to_dataset=argv[1]; 175 string associate_file=path_to_dataset+"/associate.txt"; 176 177 ifstream fin(associate_file); 178 179 string rgb_file,depth_file,time_rgb,time_depth; 180 Mat color,depth,gray; 181 vector<Measurement> measurements;//Measurement类 存储世界坐标点(以第一帧为参考的FAST关键点) 182 //和对应的灰度图像(由color->gray)的灰度值 183 184 //相机内参 185 float cx=325.5; 186 float cy=253.5; 187 float fx=518.0; 188 float fy=519.0; 189 float depth_scale=1000.0; 190 Eigen::Matrix3f K; 191 K<<fx,0.f,cx,0.f,fy,cy,0.f,0.f,1.0f; 192 // cout<<K<<endl; 193 194 Eigen::Isometry3d Tcw=Eigen::Isometry3d::Identity(); 195 196 Mat prev_color; 197 //我们以第一幅图像为参考,对后续图像和参考图像做直接法 198 //每一副图像都会与第一帧图像做直接法计算第一帧到当前帧的R,t。 199 //但是经过更多帧后,关键点数量会减少 200 //所以实际应用时,应当规定关键点的数量少于多少时就该重新设定参考系,再次利用直接法,但是会有累计的误差需要解决 201 for(int index=0;index<10;++index) 202 { 203 cout<<"******************* loop "<<index<<" ************"<<endl; 204 fin>>time_rgb>>rgb_file>>time_depth>>depth_file; 205 // cout<<time_rgb<<" "<<rgb_file<<" "<<time_depth<<" "<<depth_file<<endl; 206 color=imread(path_to_dataset+"/"+rgb_file); 207 depth=imread(path_to_dataset+"/"+depth_file,-1);//-1 按原图像的方式存储 detph:16位存储 208 if(color.data==nullptr || depth.data==nullptr) 209 continue; 210 //转换后的灰度图为g2o优化需要的边提供灰度值 211 cvtColor(color,gray,COLOR_BGR2GRAY);//cv::cvtColor()用于将图像从一个颜色空间转换到另一个颜色空间 212 //在转换的过程中能够保证数据的类型不变 213 //即转换后的图像的数据类型和位深与源图像一致 214 215 //第一帧为世界坐标系,计算FAST关键点,为之后与当前帧用直接法计算R,t做准备 216 if(index==0)//以第一帧为参考系,计算关键点后存储测量值(关键点对应的灰度值),以此为基准跟踪后面的图像,计算位姿 217 { 218 imshow("color",color); 219 imshow("depth",depth); 220 //对第一帧提取FAST角点,为什么要这样做???? 221 vector<KeyPoint> keypoints; 222 //OpenCV提供FeatureDetector实现特征检测及匹配 223 Ptr<FastFeatureDetector> detector=FastFeatureDetector::create(); 224 detector->detect(color,keypoints); 225 226 Mat outimg; 227 drawKeypoints(color,keypoints,outimg,Scalar::all(-1),DrawMatchesFlags::DEFAULT); 228 imshow("corner",outimg); 229 230 //对于2D关键点获取3D信息,并去掉范围外的点,存储符合要求的关键点的深度值和3D信息 231 //对所有关键点挑选出符合要求且有深度值的存储到vector<Measurement> measurements为g2o边提供灰度测量值和空间点坐标 232 for(auto kp:keypoints) 233 { 234 //去掉邻近边缘处的点:考虑是否能用图画出来 235 //在离图像四条边20个像素构成的内矩阵范围内是符合要求的关键点 236 // cout<<"kp.pt.x = "<<kp.pt.x<<endl<<"kp.pt.y = "<<kp.pt.y<<endl 237 // <<"color.cols = "<<color.rows<<endl; 238 if(kp.pt.x<20 || kp.pt.y<20 || (kp.pt.x+20)>color.cols || (kp.pt.y+20)>color.rows) 239 continue; 240 //depth.ptr (cvRound(kp.pt.y))表示获取行指针 241 //cvRound(kp.pt.y)表示返回跟参数值最接近的整数值 242 //因为像素量化以后是整数,而kp.pt.y存储方式是float,所以强制转换一下即可 243 ushort d=depth.ptr<ushort> (cvRound(kp.pt.y))[cvRound(kp.pt.x)]; 244 if(d==0) 245 continue; 246 Eigen::Vector3d p3d=project2Dto3D(kp.pt.x,kp.pt.y,d,fx,fy,cx,cy,depth_scale);//3D相机坐标系(第一帧,也是世界帧) 247 float grayscale=float (gray.ptr<uchar>(cvRound(kp.pt.y))[cvRound(kp.pt.x)]); 248 measurements.push_back(Measurement(p3d,grayscale)); 249 } 250 prev_color=color.clone(); 251 continue; 252 } 253 //使用直接法计算相机运动 254 //从第二帧开始计算相机位姿g2o优化 255 chrono::steady_clock::time_point t1=chrono::steady_clock::now(); 256 // 257 poseEstimationDirect(measurements,&gray,K,Tcw); 258 chrono::steady_clock::time_point t2=chrono::steady_clock::now(); 259 chrono::duration<double> time_used=chrono::duration_cast<chrono::duration<double> >(t2-t1); 260 cout<<"direct method costs time: "<<time_used.count()<<" seconds."<<endl; 261 cout<<"Tcw = "<<Tcw.matrix()<<endl; 262 263 264 // plot the feature points 265 cv::Mat img_show ( color.rows*2, color.cols, CV_8UC3 );//目的是为了之后对比前后两帧图像的关键点数量 266 //所以建立一个可以存储pre_co和color大小的矩阵 267 //Rect参数表示坐标0,0到cols,rows那么大的矩阵 268 prev_color.copyTo ( img_show ( cv::Rect ( 0,0,color.cols, color.rows ) ) );//0列,0行->cols列,rows行,大小 269 //实际上就是把第一帧的图像拷贝到img_show中 270 //因为我们针对每一帧图像都会把第一帧图像拷贝到这里,所以这里实际上执行一次即可 271 color.copyTo ( img_show ( cv::Rect ( 0,color.rows,color.cols, color.rows ) ) );//0列,rows行->cols列 rows行 272 //在measurement容器中,随机挑选出符合要求的测量值,在img_show矩阵中对应部分进行标记(因为img_show上半部分是第一帧图像,下半部分是当前图像) 273 for ( Measurement m:measurements ) 274 { 275 if ( rand() > RAND_MAX/5 ) 276 continue; 277 Eigen::Vector3d p = m.pos_world;//将空间点转换到下一帧相机坐标系下 278 Eigen::Vector2d pixel_prev = project3Dto2D ( p ( 0,0 ), p ( 1,0 ), p ( 2,0 ), fx, fy, cx, cy ); 279 Eigen::Vector3d p2 = Tcw*m.pos_world; 280 Eigen::Vector2d pixel_now = project3Dto2D ( p2 ( 0,0 ), p2 ( 1,0 ), p2 ( 2,0 ), fx, fy, cx, cy ); 281 282 //对于超出下一帧图像像素坐标轴范围的点舍弃不画 283 if ( pixel_now(0,0)<0 || pixel_now(0,0)>=color.cols || pixel_now(1,0)<0 || pixel_now(1,0)>=color.rows ) 284 continue; 285 286 //随机获取bgr颜色,在cv::circle中,为关键点用不同的颜色圆来画出 287 float b = 255*float ( rand() ) /RAND_MAX; 288 float g = 255*float ( rand() ) /RAND_MAX; 289 float r = 255*float ( rand() ) /RAND_MAX; 290 291 //在img_show包含两帧图像上,以关键点为圆心画圆,半径为8个像素,颜色为bgr随机组合,2表示外轮廓线宽度为2,如果为负数表示填充圆 292 //pixel_prev都是世界坐标系下的坐标(以第一帧为参考系)和当前帧的对比,可以看出关键点的数量会逐渐减少 293 cv::circle ( img_show, cv::Point2d ( pixel_prev ( 0,0 ), pixel_prev ( 1,0 ) ), 8, cv::Scalar ( b,g,r ), 2 ); 294 cv::circle ( img_show, cv::Point2d ( pixel_now ( 0,0 ), pixel_now ( 1,0 ) +color.rows ), 8, cv::Scalar ( b,g,r ), 2 ); 295 //连接后两帧匹配好的点 296 cv::line ( img_show, cv::Point2d ( pixel_prev ( 0,0 ), pixel_prev ( 1,0 ) ), cv::Point2d ( pixel_now ( 0,0 ), pixel_now ( 1,0 ) +color.rows ), cv::Scalar ( b,g,r ), 1 ); 297 } 298 cv::imshow ( "result", img_show ); 299 waitKey(0); 300 } 301 302 return 0; 303 } 304 305 bool poseEstimationDirect ( const vector< Measurement >& measurements, cv::Mat* gray, Eigen::Matrix3f& K, Eigen::Isometry3d& Tcw ) 306 { 307 // 初始化g2o 308 typedef g2o::BlockSolver<g2o::BlockSolverTraits<6,1>> DirectBlock; // 求解的向量是6*1的 309 DirectBlock::LinearSolverType* linearSolver = new g2o::LinearSolverDense< DirectBlock::PoseMatrixType > (); 310 DirectBlock* solver_ptr = new DirectBlock ( unique_ptr<DirectBlock::LinearSolverType>(linearSolver) ); 311 // g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr ); // G-N 312 g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( unique_ptr<DirectBlock>(solver_ptr) ); // L-M 313 g2o::SparseOptimizer optimizer; 314 optimizer.setAlgorithm ( solver ); 315 optimizer.setVerbose( true ); 316 317 g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); 318 pose->setEstimate ( g2o::SE3Quat ( Tcw.rotation(), Tcw.translation() ) ); 319 pose->setId ( 0 ); 320 optimizer.addVertex ( pose ); 321 322 // 添加边 323 int id=1; 324 for ( Measurement m: measurements ) 325 { 326 EdgeSE3ProjectDirect* edge = new EdgeSE3ProjectDirect ( 327 m.pos_world, 328 K ( 0,0 ), K ( 1,1 ), K ( 0,2 ), K ( 1,2 ), gray 329 ); 330 edge->setVertex ( 0, pose ); 331 edge->setMeasurement ( m.grayscale ); 332 edge->setInformation ( Eigen::Matrix<double,1,1>::Identity() ); 333 edge->setId ( id++ ); 334 optimizer.addEdge ( edge ); 335 } 336 cout<<"edges in graph: "<<optimizer.edges().size() <<endl; 337 optimizer.initializeOptimization(); 338 optimizer.optimize ( 30 ); 339 Tcw = pose->estimate(); 340 }
运行结果:我们贴出一部分试验结果图:参考帧与后1至3帧对比

2.1.2 半稠密直接法
对参考帧,先提取梯度较明显的像素,然后用直接法,以这些像素为图优化边来估计相机运动。与2.1.1 稀疏直接法相比,我们把先前的稀疏特征点改成了带有明显梯度的像素。于是在图优化中增加许多的边。这些边都会参与估计相机位姿的优化问题,利用大量的像素而不单单是稀疏的特征点。
代码如下:
1 #include <iostream> 2 #include <fstream> 3 #include <list> 4 #include <vector> 5 #include <chrono> 6 #include <ctime> 7 #include <climits> 8 9 #include <opencv2/core/core.hpp> 10 #include <opencv2/imgproc/imgproc.hpp> 11 #include <opencv2/highgui/highgui.hpp> 12 #include <opencv2/features2d/features2d.hpp> 13 14 #include <g2o/core/base_unary_edge.h> 15 #include <g2o/core/block_solver.h> 16 #include <g2o/core/optimization_algorithm_levenberg.h> 17 #include <g2o/solvers/dense/linear_solver_dense.h> 18 #include <g2o/core/robust_kernel.h> 19 #include <g2o/types/sba/types_six_dof_expmap.h> 20 21 using namespace std; 22 using namespace g2o; 23 24 /******************************************** 25 * 本节演示了RGBD上的半稠密直接法 26 ********************************************/ 27 28 // 一次测量的值,包括一个世界坐标系下三维点与一个灰度值 29 struct Measurement 30 { 31 Measurement ( Eigen::Vector3d p, float g ) : pos_world ( p ), grayscale ( g ) {} 32 Eigen::Vector3d pos_world; 33 float grayscale; 34 }; 35 36 inline Eigen::Vector3d project2Dto3D ( int x, int y, int d, float fx, float fy, float cx, float cy, float scale ) 37 { 38 float zz = float ( d ) /scale; 39 float xx = zz* ( x-cx ) /fx; 40 float yy = zz* ( y-cy ) /fy; 41 return Eigen::Vector3d ( xx, yy, zz ); 42 } 43 44 inline Eigen::Vector2d project3Dto2D ( float x, float y, float z, float fx, float fy, float cx, float cy ) 45 { 46 float u = fx*x/z+cx; 47 float v = fy*y/z+cy; 48 return Eigen::Vector2d ( u,v ); 49 } 50 51 // 直接法估计位姿 52 // 输入:测量值(空间点的灰度),新的灰度图,相机内参; 输出:相机位姿 53 // 返回:true为成功,false失败 54 bool poseEstimationDirect ( const vector<Measurement>& measurements, cv::Mat* gray, Eigen::Matrix3f& intrinsics, Eigen::Isometry3d& Tcw ); 55 56 57 // project a 3d point into an image plane, the error is photometric error 58 // an unary edge with one vertex SE3Expmap (the pose of camera) 59 class EdgeSE3ProjectDirect: public BaseUnaryEdge< 1, double, VertexSE3Expmap> 60 { 61 public: 62 EIGEN_MAKE_ALIGNED_OPERATOR_NEW 63 64 EdgeSE3ProjectDirect() {} 65 66 EdgeSE3ProjectDirect ( Eigen::Vector3d point, float fx, float fy, float cx, float cy, cv::Mat* image ) 67 : x_world_ ( point ), fx_ ( fx ), fy_ ( fy ), cx_ ( cx ), cy_ ( cy ), image_ ( image ) 68 {} 69 70 virtual void computeError() 71 { 72 const VertexSE3Expmap* v =static_cast<const VertexSE3Expmap*> ( _vertices[0] ); 73 Eigen::Vector3d x_local = v->estimate().map ( x_world_ ); 74 float x = x_local[0]*fx_/x_local[2] + cx_; 75 float y = x_local[1]*fy_/x_local[2] + cy_; 76 // check x,y is in the image 77 if ( x-4<0 || ( x+4 ) >image_->cols || ( y-4 ) <0 || ( y+4 ) >image_->rows ) 78 { 79 _error ( 0,0 ) = 0.0; 80 this->setLevel ( 1 ); 81 } 82 else 83 { 84 _error ( 0,0 ) = getPixelValue ( x,y ) - _measurement; 85 } 86 } 87 88 // plus in manifold 89 virtual void linearizeOplus( ) 90 { 91 if ( level() == 1 ) 92 { 93 _jacobianOplusXi = Eigen::Matrix<double, 1, 6>::Zero(); 94 return; 95 } 96 VertexSE3Expmap* vtx = static_cast<VertexSE3Expmap*> ( _vertices[0] ); 97 Eigen::Vector3d xyz_trans = vtx->estimate().map ( x_world_ ); // q in book 98 99 double x = xyz_trans[0]; 100 double y = xyz_trans[1]; 101 double invz = 1.0/xyz_trans[2]; 102 double invz_2 = invz*invz; 103 104 float u = x*fx_*invz + cx_; 105 float v = y*fy_*invz + cy_; 106 107 // jacobian from se3 to u,v 108 // NOTE that in g2o the Lie algebra is (\omega, \epsilon), where \omega is so(3) and \epsilon the translation 109 Eigen::Matrix<double, 2, 6> jacobian_uv_ksai; 110 111 jacobian_uv_ksai ( 0,0 ) = - x*y*invz_2 *fx_; 112 jacobian_uv_ksai ( 0,1 ) = ( 1+ ( x*x*invz_2 ) ) *fx_; 113 jacobian_uv_ksai ( 0,2 ) = - y*invz *fx_; 114 jacobian_uv_ksai ( 0,3 ) = invz *fx_; 115 jacobian_uv_ksai ( 0,4 ) = 0; 116 jacobian_uv_ksai ( 0,5 ) = -x*invz_2 *fx_; 117 118 jacobian_uv_ksai ( 1,0 ) = - ( 1+y*y*invz_2 ) *fy_; 119 jacobian_uv_ksai ( 1,1 ) = x*y*invz_2 *fy_; 120 jacobian_uv_ksai ( 1,2 ) = x*invz *fy_; 121 jacobian_uv_ksai ( 1,3 ) = 0; 122 jacobian_uv_ksai ( 1,4 ) = invz *fy_; 123 jacobian_uv_ksai ( 1,5 ) = -y*invz_2 *fy_; 124 125 Eigen::Matrix<double, 1, 2> jacobian_pixel_uv; 126 127 jacobian_pixel_uv ( 0,0 ) = ( getPixelValue ( u+1,v )-getPixelValue ( u-1,v ) ) /2; 128 jacobian_pixel_uv ( 0,1 ) = ( getPixelValue ( u,v+1 )-getPixelValue ( u,v-1 ) ) /2; 129 130 _jacobianOplusXi = jacobian_pixel_uv*jacobian_uv_ksai; 131 } 132 133 // dummy read and write functions because we don't care... 134 virtual bool read ( std::istream& in ) {} 135 virtual bool write ( std::ostream& out ) const {} 136 137 protected: 138 // get a gray scale value from reference image (bilinear interpolated) 139 inline float getPixelValue ( float x, float y ) 140 { 141 uchar* data = & image_->data[ int ( y ) * image_->step + int ( x ) ]; 142 float xx = x - floor ( x ); 143 float yy = y - floor ( y ); 144 return float ( 145 ( 1-xx ) * ( 1-yy ) * data[0] + 146 xx* ( 1-yy ) * data[1] + 147 ( 1-xx ) *yy*data[ image_->step ] + 148 xx*yy*data[image_->step+1] 149 ); 150 } 151 public: 152 Eigen::Vector3d x_world_; // 3D point in world frame 153 float cx_=0, cy_=0, fx_=0, fy_=0; // Camera intrinsics 154 cv::Mat* image_=nullptr; // reference image 155 }; 156 157 int main ( int argc, char** argv ) 158 { 159 if ( argc != 2 ) 160 { 161 cout<<"usage: useLK path_to_dataset"<<endl; 162 return 1; 163 } 164 srand ( ( unsigned int ) time ( 0 ) ); 165 string path_to_dataset = argv[1]; 166 string associate_file = path_to_dataset + "/associate.txt"; 167 168 ifstream fin ( associate_file ); 169 170 string rgb_file, depth_file, time_rgb, time_depth; 171 cv::Mat color, depth, gray; 172 vector<Measurement> measurements; 173 // 相机内参 174 float cx = 325.5; 175 float cy = 253.5; 176 float fx = 518.0; 177 float fy = 519.0; 178 float depth_scale = 1000.0; 179 Eigen::Matrix3f K; 180 K<<fx,0.f,cx,0.f,fy,cy,0.f,0.f,1.0f; 181 182 Eigen::Isometry3d Tcw = Eigen::Isometry3d::Identity(); 183 184 cv::Mat prev_color; 185 // 我们以第一个图像为参考,对后续图像和参考图像做直接法 186 for ( int index=0; index<10; index++ ) 187 { 188 cout<<"*********** loop "<<index<<" ************"<<endl; 189 fin>>time_rgb>>rgb_file>>time_depth>>depth_file; 190 color = cv::imread ( path_to_dataset+"/"+rgb_file ); 191 depth = cv::imread ( path_to_dataset+"/"+depth_file, -1 ); 192 if ( color.data==nullptr || depth.data==nullptr ) 193 continue; 194 cv::cvtColor ( color, gray, cv::COLOR_BGR2GRAY ); 195 if ( index ==0 ) 196 { 197 // select the pixels with high gradiants 198 for ( int x=10; x<gray.cols-10; x++ ) 199 for ( int y=10; y<gray.rows-10; y++ ) 200 { 201 Eigen::Vector2d delta ( 202 gray.ptr<uchar>(y)[x+1] - gray.ptr<uchar>(y)[x-1], 203 gray.ptr<uchar>(y+1)[x] - gray.ptr<uchar>(y-1)[x] 204 ); 205 if ( delta.norm() < 50 ) 206 continue; 207 ushort d = depth.ptr<ushort> (y)[x]; 208 if ( d==0 ) 209 continue; 210 Eigen::Vector3d p3d = project2Dto3D ( x, y, d, fx, fy, cx, cy, depth_scale ); 211 float grayscale = float ( gray.ptr<uchar> (y) [x] ); 212 measurements.push_back ( Measurement ( p3d, grayscale ) ); 213 } 214 prev_color = color.clone(); 215 cout<<"add total "<<measurements.size()<<" measurements."<<endl; 216 continue; 217 } 218 // 使用直接法计算相机运动 219 chrono::steady_clock::time_point t1 = chrono::steady_clock::now(); 220 poseEstimationDirect ( measurements, &gray, K, Tcw ); 221 chrono::steady_clock::time_point t2 = chrono::steady_clock::now(); 222 chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>> ( t2-t1 ); 223 cout<<"direct method costs time: "<<time_used.count() <<" seconds."<<endl; 224 cout<<"Tcw="<<Tcw.matrix() <<endl; 225 226 // plot the feature points 227 cv::Mat img_show ( color.rows*2, color.cols, CV_8UC3 ); 228 prev_color.copyTo ( img_show ( cv::Rect ( 0,0,color.cols, color.rows ) ) ); 229 color.copyTo ( img_show ( cv::Rect ( 0,color.rows,color.cols, color.rows ) ) ); 230 for ( Measurement m:measurements ) 231 { 232 if ( rand() > RAND_MAX/5 ) 233 continue; 234 Eigen::Vector3d p = m.pos_world; 235 Eigen::Vector2d pixel_prev = project3Dto2D ( p ( 0,0 ), p ( 1,0 ), p ( 2,0 ), fx, fy, cx, cy ); 236 Eigen::Vector3d p2 = Tcw*m.pos_world; 237 Eigen::Vector2d pixel_now = project3Dto2D ( p2 ( 0,0 ), p2 ( 1,0 ), p2 ( 2,0 ), fx, fy, cx, cy ); 238 if ( pixel_now(0,0)<0 || pixel_now(0,0)>=color.cols || pixel_now(1,0)<0 || pixel_now(1,0)>=color.rows ) 239 continue; 240 241 float b = 0; 242 float g = 250; 243 float r = 0; 244 img_show.ptr<uchar>( pixel_prev(1,0) )[int(pixel_prev(0,0))*3] = b; 245 img_show.ptr<uchar>( pixel_prev(1,0) )[int(pixel_prev(0,0))*3+1] = g; 246 img_show.ptr<uchar>( pixel_prev(1,0) )[int(pixel_prev(0,0))*3+2] = r; 247 248 img_show.ptr<uchar>( pixel_now(1,0)+color.rows )[int(pixel_now(0,0))*3] = b; 249 img_show.ptr<uchar>( pixel_now(1,0)+color.rows )[int(pixel_now(0,0))*3+1] = g; 250 img_show.ptr<uchar>( pixel_now(1,0)+color.rows )[int(pixel_now(0,0))*3+2] = r; 251 cv::circle ( img_show, cv::Point2d ( pixel_prev ( 0,0 ), pixel_prev ( 1,0 ) ), 4, cv::Scalar ( b,g,r ), 2 ); 252 cv::circle ( img_show, cv::Point2d ( pixel_now ( 0,0 ), pixel_now ( 1,0 ) +color.rows ), 4, cv::Scalar ( b,g,r ), 2 ); 253 } 254 cv::imshow ( "result", img_show ); 255 cv::waitKey ( 0 ); 256 257 } 258 return 0; 259 } 260 261 bool poseEstimationDirect ( const vector< Measurement >& measurements, cv::Mat* gray, Eigen::Matrix3f& K, Eigen::Isometry3d& Tcw ) 262 { 263 // 初始化g2o 264 typedef g2o::BlockSolver<g2o::BlockSolverTraits<6,1>> DirectBlock; // 求解的向量是6*1的 265 DirectBlock::LinearSolverType* linearSolver = new g2o::LinearSolverDense< DirectBlock::PoseMatrixType > (); 266 DirectBlock* solver_ptr = new DirectBlock (unique_ptr<DirectBlock::LinearSolverType> (linearSolver) ); 267 // g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr ); // G-N 268 g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg (unique_ptr<DirectBlock> (solver_ptr) ); // L-M 269 g2o::SparseOptimizer optimizer; 270 optimizer.setAlgorithm ( solver ); 271 optimizer.setVerbose( true ); 272 273 g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); 274 pose->setEstimate ( g2o::SE3Quat ( Tcw.rotation(), Tcw.translation() ) ); 275 pose->setId ( 0 ); 276 optimizer.addVertex ( pose ); 277 278 // 添加边 279 int id=1; 280 for ( Measurement m: measurements ) 281 { 282 EdgeSE3ProjectDirect* edge = new EdgeSE3ProjectDirect ( 283 m.pos_world, 284 K ( 0,0 ), K ( 1,1 ), K ( 0,2 ), K ( 1,2 ), gray 285 ); 286 edge->setVertex ( 0, pose ); 287 edge->setMeasurement ( m.grayscale ); 288 edge->setInformation ( Eigen::Matrix<double,1,1>::Identity() ); 289 edge->setId ( id++ ); 290 optimizer.addEdge ( edge ); 291 } 292 cout<<"edges in graph: "<<optimizer.edges().size() <<endl; 293 optimizer.initializeOptimization(); 294 optimizer.optimize ( 30 ); 295 Tcw = pose->estimate(); 296 }
分析:1)参与估计的像素像是固定在空间中一样。当相机旋转时,它们的位置似乎没有发生变化。这代表了我们估计的相机运动是正确的。
2)相比于特征点法,直接法完全依靠优化来求解相机位姿。
直接法优缺点总结
优点:1)可省去计算特征点、描述子的时间。
2)只要求有像素梯度即可,不需要特征点。
因此,直接法可以在特征点缺失的场合下使用,比较极端的例子是只有渐变的一幅图像,它可能无法提取角点类特征,但可以用直接法估计它的运动。
3)可以构建半稠密乃至稠密的地图,这是特征点法无法做到。
缺点:1)非凸性。直接法完全依靠梯度搜索,降低目标函数来计算相机位姿。其目标函数中需要取像素点的灰度值,而图像是强烈非凸的函数,这使得优化算法容易进入极小,只在运动很小时直接法才能成功。
2)单个像素没有区分度。
3)灰度值不变是很强的假设。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号