「Note」 wqs 二分

最大标志：选择恰好 \(K\) 个，使什么东西最优。

就比如说 \(f_{i,j}\) 表示前 \(i\) 个数里选 \(j\) 个的最优解。直接求解复杂度很寄。

如果 \(f_{n,x}\) 在坐标系里画出的是一个凸函数(\(x\) 是取了多少个值)，那么就可以进行 wqs 二分。

我们想要求当 \(x=K\) 时的解，因为是凸函数所以二分斜率，去用这个斜率切凸包，看对应的横坐标是什么。

具体的就是每个因为形如 \(y=kx+b\)，其中 \(kx\) 就是要在每次选的时候增加 \(k\) 的代价。

其实原理看看就行。然后还有细节。

1. 二分的数据。因为正常情况下 \(f_{i,j}\) 都是整数，所以斜率是整数，所以就在整数内二分就行。如果 \(f_{i,j}\) 可能会有小数的情况，这时候就实数二分。
2. 如果凸函数上有三点共线，那么直接二分是可能二分不到的。这时候需要自己分析选这条线段的哪一边）

题吧也没做几个好的。

P5896 [IOI2016]aliens

给一个 \(n\times n\) 的网格图，上面有一些关键点，需要以主对角线为对角线，画若干个正方形，求最小覆盖多少个方格使得所有点被覆盖。

emmmm，我不想写了。但是我有一个非常强的题解挂在上面。

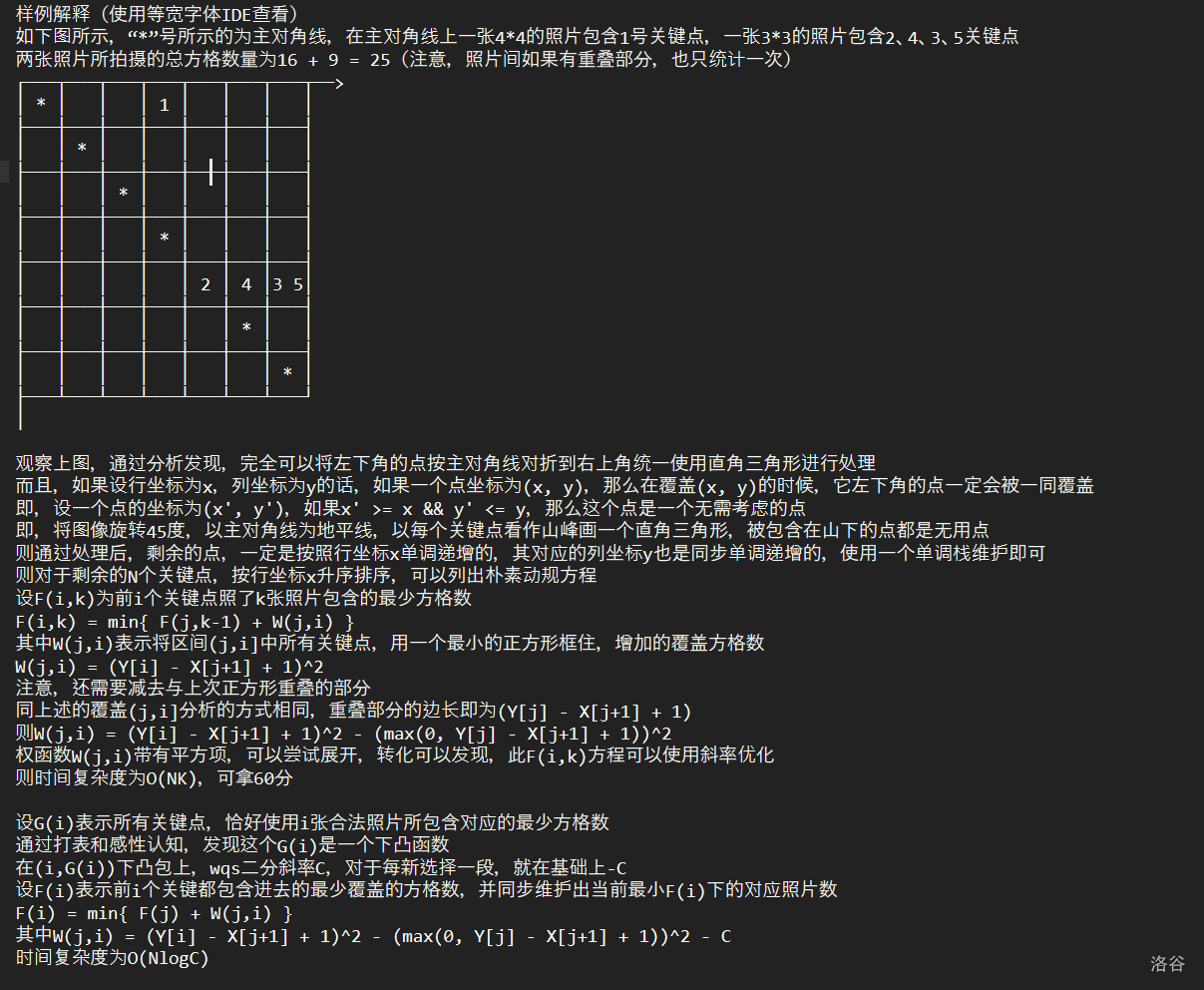
反正就是自己乱感性理解凸性，然后就斜率优化就行。

Submission

P5308 [COCI2018-2019#4] Akvizna

\(f_{i,j}\) 表示剩 \(i\) 个人，花了 \(k\) 轮的最大收益。

\(f_{i,j}=f_{k,j-1}+\frac {i-k}{i}\)

感性理解凸性，直接斜率优化www

Submission

P4983 忘情

双倍经验link

CF802O April Fools' Problem (hard)

被我扔到了模拟赛里。

就是首先考虑用 wqs 二分，感性理解凸性（肯定是增加量越大打印题目越少）

然后我们考虑如何找最优策略。

有两种情况，一种是 \(a\) 待匹配，另一种是贪心的选一个 \(a\) 匹配，用一个堆维护就行。