各种多项式和生成函数科技题
\(\LaTeX\) 渲染的速度较慢,请稍等
或许更好的阅读体验
更新记录
upd on 2023.1.3: 新建 md 文档, 添加第一道题。
upd on 2023.1.8: 添加 8 道题
upd on 2023.2.1:中间更新过好几次,忘了多少次了,反正现在有 29 道题
[THUPC2017] 小 L 的计算题
题意:\(\displaystyle f_k=\sum_i^n {a_i}^k \pmod {998244353}\),求 \(f_{1\dots k}\)
题解: 构造生成函数,\(\displaystyle F(x)=\sum _{i\geq 0}^\infty x^i \sum_{j=1}^n {a_j}^i\)
$\displaystyle F(x)=\sum_i ^\infty \sum_j^n (xa_j)^i $
\(\displaystyle F(x)=\sum _{j=1}^n \sum _{i=0 }^\infty (xa_j)^i\)
$\displaystyle F(x)=\sum_{j=0}^n \frac {xa_j}{1-xa_j} $(等比数列求和)
然后到这里就可以分治+NTT 算了,具体就是分别维护分子和分母。
然后可以接着推:
$\displaystyle F(x)=\frac {\sum_{j=1}^n x a_j\prod _{i\not =j}(1-xa_i)}{\prod _{i=1}^n(1-xa_i)} $
其中分母部分求个导就是 \(\displaystyle \sum _{j=1}^n -xa_j \prod _{i\not = j} (1-xa_j)\)
这个部分就是分子的相反数。 所以只需要给分母分治+NTT算出来,分母求个导,再取个负就是分子了。然后还需要多项式求逆就完事了
P5488 差分与前缀和
题面:对于长度为 \(n\) 的数组 \(a\),求出其 \(k\) 阶前缀和或差分数组。
题解:
设序列 \(a\) 的生成函数 \(A(x)=\sum \limits _{i=1} a_i x^i\)
如果是前缀和的话,就是需要将它乘上 \(G(x)=1+x^1+x^2+\dots +x^\infty\)
等比数列求和公式告诉我们:\(G(x)=\frac{1}{1-x}\)
所以 \(k\) 阶前缀和就是乘上 \(G^k(x)\)
如果是差分的话,就是要乘上 \(1-x\) 。
所以 \(k\) 阶差分就是乘 \(k\) 次。
然后应该一些多项式科技就能解了不过我没写。
首先是前缀和的式子:
根据广义二项式定理: \((1-x)^\alpha=\sum\limits _{i=0}^\infty(-1)^i \dbinom{\alpha }{i}x^i\)
然后开始乱推
\((1-x)^{-k}=\sum\limits_{i=0}^\infty (-1)^i\dbinom{-k}{i}x^i\)
\(=\sum\limits (-1)^i\frac {(-k)(-k-1)(-k-2)\dots (-k-i+1)}{i!}x^i\)
然后全都提出个负号。
\(=\sum\limits_{i=0}^\infty (-1)^{2i}\dbinom{k+i-1}{i}x^i\)
\(=\sum \limits _{i=0}^\infty \dbinom{k+i-1}{i}x^i\)
然后就是直接和 \(A(x)\) 卷起来就行了。
然后咱们看差分。
\((1-x)^k=\sum\limits _{i=0}^\infty (-1)^i\dbinom{k}{i}x^i\)
这个直接和 \(A(x)\) 卷起来就行。
P4451 [国家集训队]整数的lqp拆分
假设 \(g_n\) 表示所有数字和 \(n\) 的权值和,那么就有 \(\sum \limits _{i=0}^{n} g_ifib_{n-i}\)
特别的,令 \(g_0=1\),然后是设 \(G(x)\) 为 \(g\) 的生成函数。
\(\displaystyle G(x)=1+\sum_{i=1}^\infty x^i\sum_{j=0}^i g_{j}fib_{i-j}\)
\(G(x)=\sum\limits _{i=0}^\infty ([i==0]+\sum _{j=0}^{i}g_jfib_{i-j})x^i\)
里面明显有个卷积,设斐波那契数列的生成函数为 \(F(x)\)
\(G(x)=1+F(x)G(x)\)
\(G(x)=\frac {1}{1-F(x)}\)
然后众所周知的斐波那契数列的推导:\(x^2F(x)+xF(x)+x=F(x)\)
\(F(x)=\frac{x}{-x^2-x+1}\)
然后代入 \(G(x)=\frac {1}{1-\frac {x}{-x^2-x+1}}\)
然后经过推导(懒得推了)\(G(x)=1-\frac {x}{x^2+2x-1}\)
然后就来解决 \(\frac {-x}{x^2+2x-1}\)
就是设方程 \(x^2+2x-1=0\) 的两根 \(x_1,x_2\)。
\(\frac {-x}{x^2+2x-1}=\frac {-x}{(x-x_1)(x-x_2)}\)
\(=\frac {-x}{(x_1-x_2)}\times(\frac {x_1-x_2}{(x-x_1)(x-x_2)})\)
\(=\frac {-x}{x_1-x_2}\times (\frac {1}{x-x_1}-\frac {1}{x-x_2})\)
然后把括号里面的部分的常数项提成 \(1\)。
\(=\frac {x}{x_1-x_2}(\frac {1}{x_1}\frac {1}{1-\frac {1}{x_1}x}-\frac {1}{x_2}\frac {1}{1-\frac {1}{x_2}x})\)
里面的两部分为等比数列的求和公式。
所以就能拆成 \(\frac {1}{x_1-x_2}\sum\limits_{i=1} (\frac {x^i}{{x_1}^i}-\frac {x^i}{{x_2}^i})\)
所以第 \(n\) 项系数为 \(\frac {1}{x_1-x_2}(\frac {1}{{x_1}^n}-\frac {1}{{x_2}^n})\)
把数字代入,\(\frac {\sqrt 2}{4}[(1+\sqrt 2)^n-(1-\sqrt 2)^n]\)
通项有了,然后 \(\sqrt 2\) 可以暴力求, \(n\) 要 \(\mod mod-1\)
P4705 玩游戏
假期望,就是求 \(\frac {1}{nm}\sum\limits _{i=1}^n\sum\limits_{j=1}^m(a_i+b_j)^k\)
然后拆开就是 \(\sum\limits_{i=1}^n\sum\limits_{j=1}^m\sum\limits_{t=0}^{k} a_i^tb_j^{k-t}\dbinom{k}{t}\)
调换一下枚举顺序就是 \(k!\sum\limits_{t=0}^kt!\sum\limits_{i=1}^na_i^t(k-t)!\sum\limits_{j=1}^mb_j^{k-t}\)
然后后面两个是卷积的关系,所以只需要快速求出 \(\sum\limits_{i=1}^na_i^k\)
这个在[THUPC2017] 小 L 的计算题 说过了。
P4389 付公主的背包
对于单个物品,转移方程的生成函数为 \(G(x)=\sum\limits_{i=0}^\infty [i\mod v=0]x^i\)
如果是多个就是把它们都乘起来。
\(G(x)=\sum\limits_{i=0}^\infty x^{iv} =\frac {1}{1-x^v}\)
依次乘起来是不行的,考虑取 \(\ln\) ,然后再 \(\exp\)
设 \(\ln (G(x))=F(x)\)
\(F'(x)=\frac {G'(x)}{G(x)}=(1-x^v)\sum\limits_{i=1}^\infty vix^{vi-1}\)
\(=\sum\limits_{i=1}^\infty vx^{vi-1}\)
然后把 \(F(x)\) 积分一下就行。 由于 \(F(x)\) 的项数为 \(\frac {n}{v}\),所以加法的复杂度为 \(O(m\ln n)\)
P2000 拯救世界
把所有状态下的生成函数都写出来.
\(F_1(x)=\frac {1}{1-x^6}\)
\(F_2(x)=\frac {1-x^{10}}{1-x}\)
\(F_3(x)=\frac{1-x^6}{1-x}\)
\(F_4(x)=\frac {1}{1-x^4}\)
\(F_5(x)=\frac {1-x^8}{1-x}\)
\(F_6(x)=\frac {1}{1-x^2}\)
\(F_7(x)=1+x\)
\(F_8(x)=\frac {1}{1-x^8}\)
\(F_9(x)=\frac 1 {1-x^{10}}\)
\(F_{10}(x)=\frac {1-x^4}{1-x}\)
我打这些玩应的意义是什么啊
总之你知道这些玩应乘起来得 \(\frac {1}{(1-x)^5}\)
然后这个东西等于 \(\sum \limits_{i=0}^\infty \dbinom{5+i-1}{i}x^i\)
这是个重要的结论(应该好多题都用
证明:
\(\frac {1}{(1-x)^n}=(1-x)^{-n}\)
根据广义二项式定理, \((1-x)^{-n}=\sum\limits_{i=0}^{\infty} \dbinom{-n}{i}{(-x)}^i\)
\(=\sum\limits_{i=0}^\infty \frac {(-n)(-n-1)(-n-2)\dots(-n-i+1)}{i}x^i\)
分子的所有式子都提出个负号。
\(=\sum\limits_{i=0}^\infty (-1)^i\dbinom{n+i-1}{i}(-x)^i\)
\(=\sum\limits_{i=0}^\infty \dbinom{n+i-1}{i}x^i\)
然后第 \(n\) 项系数就是 \(\dbinom{5+n-1}{n}=(n+1)(n+2)(n+3)(n+4)\)
所以还需要用 FFT 写个高精乘
P4841 [集训队作业2013]城市规划
设 \(n\) 个点的无向图的数量为 \(g_n\),\(n\) 个点的无向连通图的 \(f_n\)
显然,\(g_n=2^{\dbinom{n}{2}}\)
然后还有 \(\displaystyle g_n=\sum _{i=1}^{n} \dbinom {n-1} {i-1} f_i g_{n-i}\)
拆开式子
\(\displaystyle \frac{g_n}{(n-1)!}=\sum_{i=1}^n \frac{f_i}{(i-1)!} \frac{g_{n-i}}{(n-i)!}\)
设三个生成函数 : \(G(x)=\sum \limits _{i=1} \frac {g_i}{(i-1)!},H(x)=\sum\limits_{i=1} \frac {g_i}{i!},F(x)=\sum\limits _{i=1}\frac {f_i}{(i-1)!}\)
显然 \(F(x)=G(x)H^{-1}(x)\)
然后就能求 \(F(x)\),然后 \(f_n\) 也能解了。
CF438E The Child and Binary Tree
设 \(g_i\) 表示 \(i\) 是否在集合里,\(f_i\) 表示权值和为 \(i\) 的方案数
\(f_{n}=[n==0]+\sum\limits _{i=1}^n g_i\sum\limits_{i=1}^{n-i} f_jf_{n-i-j}\)
设 \(f_i\) 和 \(g_i\) 的生成函数分别为 \(F(x)\) 和 \(G(x)\)
显然可以看出 \(F=GF^2+1\)
然后有种让人想用求根公式的冲动,但是经过题解提醒发现 \(G(x)\) 不能求逆(零次项为零),所以只能硬解
同时乘 \(G\)
\(G^2F^2-GF+G=0\)
\((GF-\frac 1 2)^2=\frac 1 4 -G\)
\(GF=\frac 1 2 ±\sqrt{\frac 1 4-G}\)
观察发现当取正号时零次项不相同,所以舍掉留负号。
\(F=\frac {2}{1+\sqrt{1-4G}}\)
[HAOI2018]染色
看着“恰好” 就知道是二项式反演www
令 \(g(i)\) 表示钦定 \(i\) 种颜色恰好 \(S\) 次。
\(g_i=\dbinom m i \frac {n!}{S!(n-iS)!}(m-i)^{n-iS}\)
首先从 \(m\) 种颜色中选出 \(i\) 种,然后从全排列中删掉钦定的相同颜色和不考虑的,然后再让不考虑的全排列
设 \(f_{i}\) 表示恰好 \(i\) 种出现 \(S\) 次
二项式反演
\(f_i=\sum\limits_{j=i}^m(-1)^{j-i}\frac {j!}{(j-i)!i!}g_j\)
\(=i!\sum\limits_{j=i}^{m} \frac {(-1)^{j-i}}{(j-i)!}g_jj!\)
\(=i!\sum\limits_{j=0}^{m-i}\frac {(-1)^j}{j!}g_{j+i}(j+i)!\)
然后把其中一个反转一下就能卷积了。
感觉好多套路题www
还没做到智慧的部分
好困
[MtOI2018]情侣?给我烧了!(加强版)
我终于写到这题了hhh
6Bit :谁说情侣必须是一男一女的?
这个梗我看一次乐一次,我笑点好低233
然而这个梗诞生的时候是讲二项式反演,但是我当时根本没写这题,后来咕咕咕了大半年才补上
困了不想写了,咕咕咕。
以下为正文。
首先是简化版:
考虑二项式反演 ,设 \(f_k\) 为钦定 \(k\) 对情侣卿卿我我的方案数。
\(f_k=\dbinom{n}{k}\dbinom{n}{k} k!2^k(2n-2k)!\)
根据二项式反演。
\(g_k\) 表示恰好 \(k\) 对情侣和和睦睦的方案数。
\(g_k=\sum\limits_{i=k}^n \dbinom{i}{k} (-1)^{i-k} f_k\)
然后化简
\(g_{k}=\sum\limits_{i=k}^n\dbinom{i}{k}(-1)^{i-k}\dbinom{n}{i}\dbinom{n}{i}i!2^i(2n-2i)!\)
\(g_k=\sum\limits_{i=k}^n (-1)^{i-k}\frac{i!n!n!}{k!(i-k)!(n-i)!i!(n-i)!i!}i!2^i(2n-2i)!\)
\(g_k=(n!)^2\sum\limits_{i=k}^n (-1)^{i-k} \frac {1}{k!(i-k)!((n-i)!)^2}2^i(2n-2i)!\)
然后平移 \(i\)
\(g_k=\frac {(n!)^2}{k!}\sum\limits_{i=0}^{n-k} \frac {(-1)^i2^i}{i!} \frac {(2n-2i-2k)!}{((n-i-k)!)^2}\)
这是个卷积的形式,但是显然即使你不会卷积这个也能过简化版。
然后是强化版。
令 \(G(x)\) 为 \(g_i\) 的生成函数,\(F(x)\) 为 \(f_i=\frac {{(-1)^i}2^i}{i!}\) 的生成函数,\(H(x)\) 为 \(h_i=\frac {(2i)!}{(i!)^2}\) 的生成函数。
然后发现最终答案就是 \(F(x)H(x)\) 再成上个系数。
然后大家都是说 \(F(x)\) 是显然的,但是我不会wwww
我:为啥 \(\frac {1}{n!}\) 的生成函数的封闭形式是 exp 啊
红太阳:你直接泰勒展开就完事了
我:啊?啊......啊!
把 \(e^x\) 在 \(x=0\) 处泰勒展开,得到 \(\sum\limits _{i=0}^\infty \frac {e^0}{i!} x^i\)。
所以就是 \(\sum\limits _{n=0}^\infty \frac {1}{n!}x^n\)
所以上面的 \(F(x)\) 的封闭形式是 \(e^{-2x}\)
不好整的是 \(H(x)\)
\(H(x)=\sum\limits_{i=0}^\infty \dbinom{2i}{i} x^i\)
然后需要用到一个高妙的等式: \(\frac {\dbinom{2n}{n}}{4^n}=\dbinom{n-\frac {1}{2}}{n}\)
这个等式我在之后处理一些长相丑陋的二项式经常用到。不过当时都是反着用的所以现在想不起来。
\(\dbinom {n-\frac {1}{2}}{n} = \frac {(n-\frac{1}{2})(n-\frac{1}{2}-1)\dots(n-\frac{1}{2}-n+1)}{n!}=\frac {(n-1)(n-3)(1)}{n!}2^n=\frac {(n-1)(n-3)\dots(1)\times (2)(4)\dots(2n)}{(n!)^2}4^n=\dbinom{2n}{n}4^n\)
所以有上式成立
所以有 \(H(x)=\sum\limits_{n=0}^\infty{ \dbinom {n-\frac1 2}{n}4^nx^n}\)
\(=\sum\limits_{n=0}^\infty\dbinom{-\frac 1 2}{n} 4^n x^n (-1)^n\)(理由是把里面拆开,同时提出负号)\(=(1-4x)^{-\frac 1 2}\)\(=\frac {1}{\sqrt {1-4x}}\)
然后把两个生成函数乘到一起
\(F(x)H(x)=\frac {e^{-2x}}{\sqrt {1-4x}}\)
完蛋求导我写不明白。
令 \(D(x)=\frac {e^{-2x}}{\sqrt{1-4x}}\)
\(D^2(x)=\frac {e^{-4x}}{1-4x}\)
\(D^2(x)(1-4x)=e^{-4x}\)
同时求导
\((D^2(x))'(1-4x)-4D^2(x)=(e^{-4x})'\)
\((2D'(x)D(x))(1-4x)-4D^2(x)=-4e^{-4x}\)
\(2D'(x)D(x)-8xD'(x)D(x)-4D^2(x)=-4D^2(1-4x)\) (等式右边是将开始的那个东西带进去了)
化简一下:
\(D'(x)-4xD'(x)=8xD(x)\)
然后写成递推公式的形式就是:\(d_{n+1}(n+1)-4nd_nx^n=8d_{n-1}x^n\)
\(nd_n=4d_{n-1}(n-1)+8d_{n-2}\)
然后就是推一下,最后的结果为 \(\frac {(n!)^2}{k!}d_{n-k}\)
【CSGRound2】开拓者的卓识
第一步,首先考虑的是每个点对答案的贡献。
也就是转化成每个点,开始向外扩展 \(k\) 步的方案数
也就是说 \(ans_{1,i}=\sum\limits_{j=1}^i a_{j} \dbinom{j+k-1}{k-1} \dbinom{i-j+k}{k-1}\)
令 \(A_j=a_j\dbinom{j+k-1}{k-1}\),\(B_j=\dbinom{j+k}{k-1}\)
然后卷起来
[AGC005F] Many Easy Problems
巧妙的思路。
第一个巧妙的思路是假设 \(c_{(i,j)}\) 表示 \(i\) 节点为大小为 \(j\) 的点集可以做出的贡献。这样 \(f(k)\) 为 $\sum c_{(i,k)}。
然后考虑求解。如果一个点集形成的联通块包含 \(i\) ,就说明 \(i\) 能造成贡献。 所以凡是选择的点集仅仅在 \(i\) 的某一个儿子的子树内,或者在整个以 \(i\) 为根的子树外,就不能形成贡献。
所以: \(c_{(i,j)}=\dbinom{n}{j}-\sum\limits_{v\in son_i} \dbinom{siz_v}{j}-\dbinom{n-siz_i}{j}\)
然后你发现还是不会。这就要继续转化:考虑把相同子树大小的点合并到一起,计算贡献,因为它们形成的组合数是相同的
然后设 \(cnt_i\) 表示子树大小为 \(i\) 的点的数量。\(cnt'_i\) 表示子树大小为 \(n-siz_i\) 的点的数量。所以设 \(c_{i,j}\) 的和为 \(c_j\)。
\(\displaystyle c_j=n\dbinom{n}{j}-\sum_{j\leq i<n}(\dbinom{i}{j}cnt_i+\dbinom{i}{j}cnt'_i)\)
\(\displaystyle =n\dbinom{n}{j}-\sum_{j\leq i <n}\frac{i!}{j!(i-j)!} (cnt_i+cnt'_i)\)
\(\displaystyle=n\dbinom{n}{j}-\frac {1}{j!}\sum_{0\leq i<n-j}\frac{(i+j)!(cnt_{i+j}+cnt'_{i+j})}{j!}\)
左边把一个式子转一下就是卷积
P4173 残缺的字符串
伪装成字符串的贩毒题()
据说是套路。
假设两个字符串的匹配函数 \(dis(A,B)\),当他们为 \(0\) 说明能完全匹配上,否则不行。
然后 \(dis(A,B)=\sum\limits_{0\leq i<n} (A[i]-B[i])^2A[i]B[i]\)
前面的平方项的意思是强制转正,防止正负抵消。乘上当前字符是如果有一个为通配符,将通配符设为 \(0\),乘进去可以认定为相等。
然后设 \(f(i)\) 表示第 \(i\) 位开始是否能完全匹配,\(f(i)=dis(A,B[i,i+m-1])\)
\(f(i)=\sum\limits_{0\leq j <m} (A[j]-B[i+j])^2A[j]B[i+j]\)
手动展开 \(f(i)=\sum\limits_{0\leq j<m} A[j]^3B[i+j]-2\sum\limits_{0\leq j} A[j]^2B[j+i]^2+\sum\limits_{0\leq j}A[j]B[i+j]^2\)
这是三个典型的卷积形式。所以就做出来了
U107257 【模板】二维 FFT
不懂原理。但是好象是因为 FFT 是线性变换。 所以先对行 DFT,然后对列 DFT,然后整体乘起来,然后对列 IDFT,再对行 IDFT
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=4000;
namespace POLY
{
ll A[maxn],B[maxn],pos[maxn],S[maxn];
const int mod=998244353,g=3,ginv=332748118;
ll ksm(ll x,int y)
{
ll ret=1;
while(y)
{
if(y&1) ret=ret*x%mod;
x=x*x%mod; y>>=1;
}
return ret;
}
int pre(int n,int m)
{
int lim=0;
while((1<<lim)<=n+m) lim++;
for(int i=0;i<=(1<<lim);i++)
pos[i]=(pos[i>>1]>>1)|((i&1)<<(lim-1));
return lim;
}
void NTT(ll *f,ll n,int opt)
{
for(int i=0;i<n;i++) if(i<pos[i]) swap(f[i],f[pos[i]]);
for(int i=1;i<n;i<<=1)
{
ll step=ksm((opt>0?g:ginv),(mod-1)/(2*i));
for(int j=0;j<n;j+=i+i)
{
ll cur=1;
for(int k=j;k<j+i;k++)
{
int gx=f[k],hx=1ll*cur*f[k+i]%mod;
f[k]=(gx+hx)%mod;f[k+i]=(gx-hx+mod)%mod;
cur=cur*step%mod;
}
}
}
if(opt==-1)
{
int ninv=ksm(n,mod-2);
for(int i=0;i<n;i++) f[i]=f[i]*ninv%mod;
}
}
}
int n;
using POLY::mod;
ll f[maxn][maxn],g[maxn][maxn],F[maxn][maxn],G[maxn][maxn],ans[maxn][maxn],anss[maxn][maxn];
int main()
{
scanf("%d",&n);
for(int i=0;i<=n;i++)
{
for(int j=0;j<=n;j++)
scanf("%lld",&f[i][j]);
}
for(int i=0;i<=n;i++)
{
for(int j=0;j<=n;j++)
scanf("%lld",&g[i][j]);
}
int len=(1<<POLY::pre(n,n));
for(int i=0;i<=n;i++) POLY::NTT(f[i],len,1),POLY::NTT(g[i],len,1);
for(int i=0;i<=len;i++)
{
for(int j=0;j<=len;j++)
{
F[j][i]=f[i][j]; G[j][i]=g[i][j];
}
}
for(int i=0;i<=len;i++) POLY::NTT(F[i],len,1),POLY::NTT(G[i],len,1);
for(int i=0;i<=len;i++)
{
for(int j=0;j<=len;j++)
ans[i][j]=F[i][j]*G[i][j]%mod;
POLY::NTT(ans[i],len,-1);
for(int j=0;j<=len;j++)
anss[j][i]=ans[i][j];
}
for(int i=0;i<=len;i++)
{
for(int j=0;j<=len;j++)
anss[j][i]=ans[i][j];
}
for(int i=0;i<=len;i++) POLY::NTT(anss[i],len,-1);
for(int i=0;i<=2*n;i++)
{
ll ret=0;
for(int j=0;j<=len;j++) ret^=anss[i][j];
printf("%lld ",ret);
}
printf("\n");
for(int i=0;i<=2*n;i++)
{
ll ret=0;
for(int j=0;j<=len;j++)
ret=ret^anss[j][i];
printf("%lld ",ret);
}
printf("\n");
}
[ABC265Ex] No-capture Lance Game
6Bit:这题你们自己研究一下吧。
我记得当时被另外一个高妙的做法折磨傻了。
两个车放置的方式不同做法肯定不同。
如果他们全是对向放置的,那就是普普通通的 Nim 游戏。
如果是反向放置的,那就是磨谁的步数多。步数多的即使 Nim 游戏输了也能吧对方磨死。
所以设方程为 \(f[i][j][k]\) 表示做了 \(i\) 行,对向的部分异或和为 \(j\),反向的部分 A 比 B 少 \(k\),
转移就是 \(f[i][j][k]->f[i+1][j\oplus (x-y)][k](x>y)\\->f[i+1][j][k+(n-y)-(x-1)](x<y)\)
\(x,y\) 分别为两人的棋子的位置。
然后容易发现的是第二维是个异或卷积,第三位也是个卷积。所以这就是二维 FFT 的用处。而行之间的转移可以用矩阵快速幂。还有一种就是把行和列 DFT 完了之后都变成 \(k\) 次幂再乘起来效果是一样的
P5110 块速递推
手推斐波那契数列。在上面 P4451 [国家集训队]整数的lqp拆分 这题写过了,不写了。
[CF827E]Rusty String
我们可以用上一道字符串匹配中用到的套路,设 \(F(i)\) 表示前段长度为 \(i\) 时是否能匹配上。(0 为能匹配,其他均为不行)
\(F(i)=\sum\limits_{1\leq j\leq n-i} A[i+j]A[j](A[i+j]-A[j])^2\)
然后等式拆开再卷积三次就行。
但是这题不行。因为这里我们把 ? 看作通配符,这样可能同一位置的两个 ? 与不同的字符匹配。这样不符合题意。
我们可以找到一个性质:如果前端长度为 \(i\) 的是矛盾的,那么前端长度为 \(i\) 的倍数的一定存在不行的。
具体的可以看这张图:
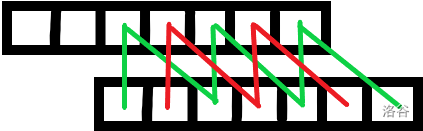
如果是河里的,那么同种颜色表示的字符一定是相同的。错开成 \(i\) 的倍数之后也还是让红色和绿色的分别对应,也就是说一定也河里。
如果一种颜色中出现了两种确定的不相同的字符,那么一定能做到错开之后让不同字符对应到一起使其不合理。
所以排除掉矛盾的方式就是找到所有倍数,如果有至少一个是算出来就不行的,那么这个就一定不行。\(O(n\ln n)\) 判断。
P5075 [JSOI2012] 分零食
设 \(f(i)\) 为分到 \(i\) 块糖的小朋友的幸福度。求法写在题面了。
假设 \(f(i)\) 的生成函数为 \(F(x)\),那么 \((F(x)-1)^k\) 为 有k个分到了糖的小盆友的总幸福值。
所以 \(ans=\sum\limits_{i=0}^{A} (F(x)-1)^i\)
\(=\frac{1-(F(x)-1)^A}{2-F(x)}\)
没了,然后里层 NTT 要用 998244353 取模,外层用给的 P ,给我恶心到了。
P5395 第二类斯特林数·行
第二类斯特林数:把 \(n\) 个不同元素分进 \(m\) 个相同的集合中的方案数。
记为 \(\begin{Bmatrix}n\\m\end{Bmatrix}\)
这玩意有个最重要(?)的性质:
\(m^n=\sum\limits_{i=1}^n \dbinom {m}{i} i! \begin{Bmatrix} n\\i\end{Bmatrix}\)
很容易理解,就是把 \(n\) 个不同的元素乱放在 \(m\) 个不同的盒子,从 \(m\) 个盒子中选 \(i\) 个,\(i!\) 是给这 \(i\) 个不同的顺序,\(\dbinom m i\) 是从 \(m\) 个选 \(i\) 个非空盒子
根据二项式反演: \(\begin{Bmatrix}n\\m\end{Bmatrix}\)$ =\frac {1}{m!}\sum\limits _{i=1}^{m} (-1)^{m-i}\dbinom m i i^m $
\(\begin{Bmatrix} n \\ m\end{Bmatrix} =\sum\limits_{i=1}^m \frac {(-1)^{m-i}}{(m-i)!} \frac{i^m}{i!}\)
这是卷积形式,可以 NTT 做了。
P5396 第二类斯特林数·列
设第二类斯特林数的生成函数为 \(F_k(x) =\sum\limits _{i=0}^{\infty}\)\(\begin{Bmatrix}i\\k\end{Bmatrix}\)\(x^i\)
根据第二类斯特林数的性质: \(F_k(x)=\sum\limits_{i=0}^\infty (k\begin{Bmatrix}{i-1}\\k\end{Bmatrix}+\begin{Bmatrix}i-1\\k-1\end{Bmatrix}) x^i\)
\(F_k(x) =(kF_k(x)+F_{k-1}(x))x\)
\(F_{k}(x)=\frac {x} {1-kx} F_{k-1}(x)\)
因为 \(F_0(x)=1\)
所以就是 \(F_m(x)=\frac{x^m}{\prod _{i=1}^m (1-ix)}\)
分治 NTT 即可。
P4091 [HEOI2016/TJOI2016]求和
推式子推几步就行((
\(=\displaystyle \sum_{j=0}^n 2^j (j!)\sum_{i=j}^n\begin{Bmatrix}i\\j\end{Bmatrix}\)
因为当 \(i<j\) 时, \(\begin{Bmatrix} i\\j\end{Bmatrix}=0\),所以可以直接改条件
\(=\displaystyle \sum_{j=0}^n 2^j (j!)\sum_{i=0}^n\begin{Bmatrix}i\\j\end{Bmatrix}\)
根据咱们刚才推的式子
\(=\displaystyle \sum_{j=0}^n 2^j j!\sum_{i=0}^n \sum_{k=0}^j \frac {(-1)^{j-k}k^i}{(j-k)!k!}\)
\(=\displaystyle \sum_{j=0}^n 2^j j! \sum_{k=0}^j\frac {(-1)^{j-k}\sum_{i=0}^nk^i}{(j-k)!k!}\)
\(\displaystyle =\sum _{j=0}^n2^j j!\sum_{k=0}^j\frac {(-1)^{j-k}}{(j-k)!}\frac {k^{n+1}-1}{k!(k-1)}\)
然后后面卷积,相乘一下就行。
P3760 [TJOI2017] 异或和
有趣的转化。求异或和就是所有出现奇数次的数字的异或和。
这意味着我们要求所有数字在连续和中出现的次数。
设 \(f_{i}\) 为前缀和中所有数字连续出现的次数。 \(g_{i}\) 表示连续和中所有数出现的次数。
\(g_i=\sum_{j=0}^mx f_{j} f_{j+i}\)
反转一下就是卷积的形式。
[CF1613F]Tree Coloring
简单题,但是 \(O(n\log ^2 n)\)
假设钦定 \(i\) 个点不合法的方案数为 \(f_i\),求出来 \(f_i\) 容斥一下就是答案。
最重要的性质就是一个点只能钦定一个儿子不合法。 并且所有点之间选哪个儿子互不影响。
假设我们钦定了 \(i\) 个点不合法,也就是 \(i\) 条边不合法,这样会形成 \(n-i\) 个联通块。而染色的方案数就是联通块的个数的阶乘乘以选择 \(i\) 个点的方案数。
假设一个点有 \(k\) 个儿子,那么设 \(f_i\)的生成函数为 \(F(x)\),只考虑选这个点的儿子的 \(F(x)=kx+1\),那么整棵树就是把所有的 \(F(x)\) 乘起来。
然后就能分治 NTT 了。
[ABC267Ex] Odd Sum
观察到一点就是 \(A_i\) 极小,也就是一定有一堆重复元素。然后假设 \(f_{i,j,0/1}\) 为元素为 \(i\),和为 \(j\),选出偶数/奇数个元素的方案数。
把所有的十个卷积乘起来就是答案,乘起来就是奇数卷奇数加偶数卷偶数就是新的偶数,奇数卷偶数加偶数卷奇数就是新的奇数。
需要分治进行计算。
[ABC269Ex] Antichain
我觉得这道题和动态 DP 的想法很像()
设 \(f(i,j)\) 为以 \(i\) 为根的子树选 \(j\) 个点的方案数,\(F_i(x)\) 为它的生成函数。因为一个点要么分别选子树里面的,要么只选自己,所以 $F_i(x)=x+\prod\limits_{v\in son} F_v(x) $
乘法可以用 NTT 优化,但是复杂度还是错误的,对于链或者菊花,要合并 \(O(n)\)次,很容易变成 \(O(n^2)\)
那么考虑动态 DP 的优化方式,设 \(G(x)\) 为只考虑轻儿子的方案。\(G(x)\) 是通过暴力合并重儿子的 \(F(x)\) 计算的,因为轻链最多 \(\log\) 个,所以这里的复杂度为 \(O(n\log ^2 n)\)
那么考虑如何计算每一条重链链头的 \(F(x)\)。
\(F_1(x)=G_1(x)(F_2(x))+x\\=G_1(x)(G_2(x)F_3(x)+x)+x\\\dots\\=G_1(x)(G_2(x)\dots (G_c(x)+x)\dots+x)+x\)
这里把下标换成重链链头的深度,方便理解。 \(c\) 是重链长度。
然后手动展开一下
\(\displaystyle F_1(x)=x(1+\sum_{i=1}^{c} \prod_{j=i}^n G_j(x))+\prod_{i=1}^n G_i(x)\)
这里可以分治 NTT 的过程中维护两个多项式,一个表示前缀积的和,另一个表示所有的积。乘的时候合并就行了。
注意方向就行。
我觉得我现在写多项式越来越丑了,但是 vector 真香。
有点想不通为啥红太阳写那么短()
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2000030;
namespace POLY
{
ll A[maxn],B[maxn],pos[maxn],S[maxn];
const int mod=998244353,g=3,ginv=332748118;
ll ksm(ll x,int y)
{
ll ret=1;
while(y)
{
if(y&1) ret=ret*x%mod;
x=x*x%mod; y>>=1;
}
return ret;
}
int pre(int n,int m)
{
int lim=0;
while((1<<lim)<=n+m) lim++;
for(int i=0;i<=(1<<lim);i++)
pos[i]=(pos[i>>1]>>1)|((i&1)<<(lim-1));
return lim;
}
void NTT(ll *f,ll n,int opt)
{
for(int i=0;i<n;i++) if(i<pos[i]) swap(f[i],f[pos[i]]);
for(int i=1;i<n;i<<=1)
{
ll step=ksm((opt>0?g:ginv),(mod-1)/(2*i));
for(int j=0;j<n;j+=i+i)
{
ll cur=1;
for(int k=j;k<j+i;k++)
{
int gx=f[k],hx=1ll*cur*f[k+i]%mod;
f[k]=(gx+hx)%mod;f[k+i]=(gx-hx+mod)%mod;
cur=cur*step%mod;
}
}
}
if(opt==-1)
{
int ninv=ksm(n,mod-2);
for(int i=0;i<n;i++) f[i]=f[i]*ninv%mod;
}
}
void MUL(ll *s,ll *f,ll *h,int n,int m)
{
int lim=pre(n,m);
for(int i=0;i<=n;i++) A[i]=f[i];
for(int i=0;i<=m;i++) B[i]=h[i];
for(int i=n+1;i<=(1<<lim);i++) A[i]=0;
for(int i=m+1;i<=(1<<lim);i++) B[i]=0;
NTT(A,(1<<lim),1);NTT(B,(1<<lim),1);
for(int i=0;i<=(1<<lim)-1;i++) s[i]=A[i]*B[i]%mod;
NTT(s,(1<<lim),-1);
}
}
using POLY::mod; using POLY::ksm;
int n;
int to[maxn],nxt[maxn],head[maxn],num;
void add(int x,int y){num++;to[num]=y;nxt[num]=head[x];head[x]=num;}
int son[maxn],top[maxn],fa[maxn],siz[maxn];
void FIT(vector<ll> &f)
{
int cnt;
for(int i=0;i<f.size();i++)
if(f[i]) cnt=i;
f.resize(cnt+1);
}
void dfs1(int p,int f)
{
fa[p]=f; siz[p]=1;
for(int i=head[p];i;i=nxt[i])
{
if(to[i]==f) continue;
dfs1(to[i],p);
siz[p]+=siz[to[i]];
if(siz[to[i]]>siz[son[p]]) son[p]=to[i];
}
}
void dfs2(int p,int tp)
{
top[p]=tp;
if(son[p]) dfs2(son[p],tp);
for(int i=head[p];i;i=nxt[i])
{
int v=to[i]; if(v==fa[p]||v==son[p]) continue;
dfs2(v,v);
}
}
vector<ll> solve(int l,int r,vector<vector<ll>> &G)
{
if(l>r) {vector<ll> ret; ret.push_back(1); return ret;}
if(l==r) return G[l];
int mid=(l+r)>>1;
vector<ll> L,R,ans; L=solve(l,mid,G); R=solve(mid+1,r,G);
ans.resize(1<<POLY::pre(L.size(),R.size()));
POLY::MUL(ans.data(),L.data(),R.data(),L.size()-1,R.size()-1);
FIT(ans);
return ans;
}
struct martix{vector<ll> L,R;};
martix solve_heavy(int l,int r,vector<vector<ll>> &G)
{
if(l>r){martix ret; ret.L.push_back(1); ret.R.push_back(1); return ret;}
if(l==r)
{
vector<ll> x; x.push_back(1);
return (martix){x,G[l]};
}
int mid=(l+r)>>1;
martix Lans,Rans,ret;
Lans=solve_heavy(l,mid,G); Rans=solve_heavy(mid+1,r,G);
ret.L.resize(max(1ll<<POLY::pre(Lans.L.size(),Rans.R.size()),(ll)Rans.L.size()));
ret.R.resize(1<<POLY::pre(Lans.R.size(),Rans.R.size()));
POLY::MUL(ret.L.data(),Lans.L.data(),Rans.R.data(),Lans.L.size()-1,Rans.R.size()-1);
for(int i=0;i<(int)Rans.L.size();i++)
ret.L[i]=(ret.L[i]+Rans.L[i])%mod;
POLY::MUL(ret.R.data(),Lans.R.data(),Rans.R.data(),Lans.R.size()-1,Rans.R.size()-1);
FIT(ret.L);
FIT(ret.R);
return ret;
}
vector<ll> dfs3(int u)
{
vector<vector<ll>> light_son,heavy;
vector<ll> G;
int p=u;
while(p)
{
light_son.resize(0);
for(int i=head[p];i;i=nxt[i])
{
int v=to[i];
if(v==fa[p]||v==son[p]) continue;
light_son.push_back(dfs3(to[i]));
}
G=solve(0,light_son.size()-1,light_son);
FIT(G);
heavy.push_back(G);
p=son[p];
}
reverse(heavy.begin(),heavy.end());
martix tmp=solve_heavy(0,heavy.size()-1,heavy);
FIT(tmp.L);FIT(tmp.R);
vector<ll> ret; ret.resize((1<<POLY::pre(tmp.L.size(),2))+10);
vector<ll> xx; xx.resize(2); xx[0]=0,xx[1]=1;
POLY::MUL(ret.data(),tmp.L.data(),xx.data(),tmp.L.size()-1,1);
for(int i=0;i<(int)tmp.R.size();i++)
ret[i]=(ret[i]+tmp.R[i])%mod;
FIT(ret);
return ret;
}
int main()
{
//freopen("p.in","r",stdin);
//freopen("p.out","w",stdout);
scanf("%d",&n);
for(int i=2;i<=n;i++)
{
int x;scanf("%d",&x);
add(x,i);
}
dfs1(1,1); dfs2(1,1);
vector<ll> ans=dfs3(1);
ans.resize(n+2);
for(int i=1;i<=n;i++)
printf("%lld\n",ans[i]);
fprintf(stderr,"Time : %.3lf\n",1.0*clock()/CLOCKS_PER_SEC);
}
P5219 无聊的水题 I
昨天做这道题有点晕,今天 Tsawke 问了一个问题,我受到启发,然后这道题和下一个题就瞬间明白了。
首先是前置知识(ZSH:你看一眼 oi-wiki 就行):\(prufer\) 序列。
构造方式就是删掉标号最小的叶子(只有一个儿子的根也算),然后在序列里记上它的父亲。直到剩下两个节点。
显而易见的性质:每个点会出现度数 -1 次。能确定一个唯一的树。
然后就简单了。把 \(n\) 个数可以填多次,填进 \(n-2\) 个位置,每个数不能出现超过 \(m-1\) 次。
然后用 EGF 解决多重排列计数,把 \(\sum\limits_{i=0}^{m-1}\frac {x^i}{i!}\) 乘 \(n-2\) 次,然后再乘上 \((n-2)!\)
这就是多重集排列计数的解法。
Tsawke 问的就是这个。
P5339 [TJOI2019]唱、跳、rap和篮球
我昨天做完了洛谷上的两道 cxk 题。
考虑容斥。答案为:\(\displaystyle \sum_{i=0}^{n}(-1)^i \dbinom{n-3i}{i} S(n-3,a-i,b-i,c-i,d-i)\)
设 \(S(n,a,b,c,d)\) 为喜好分别为 \(a,b,c,d\) 的人排列在 \(n\) 个位置上的方案数。这就是上面的多重集排列。
[CF 528D] Fuzzy Search
首先考虑到只有四种字符。所以可以分四次来做。
对于每一种字符,我们定义 \(f(i)\) 为在 \(S\) 中的每 \(i\) 位置是否可以匹配。\(f(i)\) 就是如果相邻 \(k\) 个有当前字符就是 \(1\),否则是 \(0\)。\(g(i)\) 就是 \(T\) 中这一位是否是当前字符。然后求的就是 \(\sum\limits_{x=0}^m \sum\limits_{i=0}^m f(i+x)g(i)\) 翻转过来就是卷积。
然后如果答案第 \(x\) 位为 \(T\) 中含有当前字符的个数,就说明 \(x\) 位在当前字符下可以。如果 \(x\) 在四种字符下都可以,那么 \(x\) 就是可以的。
P2791 幼儿园篮球题
吐槽:其实我挺烦这个梗的。我弟这两天总看各种 cxk 鬼畜,现在看着这个梗就反胃。
要求:\(\displaystyle \sum_{i=1}^k \dbinom{m}{i} \dbinom{n-m}{k-i} i^L\)
首先是经典斯特林数的式子。
\(\displaystyle m^n= \sum_{i=1}^m \begin{Bmatrix}n\\i\end{Bmatrix} \dbinom{m}{i} i!\)
代入到下面。
\(\displaystyle =\sum_{i=1}^k \dbinom{m}{i} \dbinom{n-m}{k-i}\sum_{j=1}^i \begin{Bmatrix}L\\j\end{Bmatrix}\dbinom{i}{j} j!\\ =\sum_{j=1}^k \begin{Bmatrix}L\\j\end{Bmatrix} j!\sum_{i=j}^k \dbinom{m}{i}\dbinom{n-m}{k-i}\dbinom{i}{j}\\=\sum_{j=1}^k \begin{Bmatrix}L\\j\end{Bmatrix} j! \dbinom{m}{j} \sum_{i=j}^k \dbinom{m-j}{i-j}\dbinom{n-m}{k-i}\\= \sum_{j=1}^k \begin{Bmatrix}L\\j\end{Bmatrix} j! \dbinom{m}{j} \sum_{i=0}^{k-j} \dbinom{m-j}{i} \dbinom{n-m}{k-i-j}\)
然后利用范德蒙德卷积:\(\displaystyle \sum \dbinom{n}{i} \dbinom{m}{k-i}=\dbinom{n+m}{k}\)
\(\displaystyle =\sum_{j=1}^k \begin{Bmatrix}L\\j\end{Bmatrix}j!\dbinom{m}{j}\dbinom{n-j}{k-j}\)
这就是答案。
CF923E Perpetual Subtraction
懒得打公式捏。


#loj6289. 花朵
我做过一个跟这个几乎一模一样的题,但是还是写了好长时间/kk
菊花的转移我觉得我挺明白的,不过链上的当时也没想明白。
这个呢就是每个点有两个方程 \(F[i][j],G[i][j]\),一个表示自己没选,另一个表示自己选了。然后用矩阵转移的话需要考虑头尾分别是什么
这样比较好理解了。
还有点细节就是分治 NTT 时不要带着个 stl 的大数组下传进去,(复杂度好像会假)
#loj6672. 「XXOI 2019」惠和惠惠和惠惠惠
强调一下最后一次必为 \(0\)。题面有误
这种数居然有名字?
首先就是 \(f_{i,j}\) 表示前 \(i\) 个回合,正好 \(j\) 次正好为 \(0\)
\(f_{i,j}=\sum\limits_{k=0}^{i-1} f_{k,j-1}h(i-k)\) \(h(i)\) 表示走了 \(i\) 步,只有头和尾正好碰到 \(0\) 的方案数。只要知道了 \(h(i)\) 那只要乘 \(k\) 次即可。
现在考虑怎么求 \(h(i)\) 我们先固定第一步和最后一步,剩下的就可以随便碰到 \(0\) 了,这样我们求出来后需要右移 \(2\) 位。
那么 \(h(i) =\sum \limits_{j=0}^i \dbinom i j D(i-j)\) 意思就是选出来 \(j\) 步走 \(0\),\(D(i)\) 是卡特兰数。
这样就求完了。巨大卡常很烦人。
[ABC279Ex] Sum of Prod of Min
我们假设 \(F_k(x)\) 表示在位置 \(k\) 上的生成函数。
\(F_k(x)=\sum_\limits{i=0}^{\infty} \min(t,i)x^i\)。
\(=\sum\limits_{i=0}^{t-1}ix^i+\sum\limits_{i=t}^{\infty} \frac {x(1-x^t)}{(1-x)^2}\)
(这一步就是拿等比数列暴力合并,题解大佬都是妙妙求导但我不会/kk)
\(ans=\prod\limits_{i=1}^n F_{i}(x)\)
\(=\prod\limits_{i=1}^n\frac {x(1-x^i)}{(1-x)^2}\)
\(=(1-x)^{-2n}x^n\prod \limits_{i=1}^n (1-x^i)\)
这里涉及到一个小知识
五边形数定理:
\(\prod\limits_{i=1}^n (1-x^i) =\sum\limits_{i=0}(-1)^ix^{\frac {i(3i\pm 1)}{2}}\)
证明:不会。(
欧拉本人在过了十年之后才证明出来)
然后继续化简:
由于我们想要求次数为 \(m\) 的项,并且前面有个比较烦的 \(x^n\),所以我们干脆转化为求次数为 \(m-n\) 的项。
\(=[x^{m-n}]\sum\limits_{i=0} \dbinom{i+2n-1}{i} x^i \sum\limits_{j=0}^{\infty} f(j)x^{a(j)}\)
我们假设 \(f(i),a(i)\) 为五边形定理的系数和指数。
这里还用到一个知识点
上指标反转:\(\dbinom r k=\dbinom {k-r-1}{k}(-1)^k\)
证明:
\(\dbinom r k=\frac {r^{\underline{k}}}{k!}=\frac {r(r-1)\dots (r-k+1)}{k!}=(-1)^k \dbinom{k-r-1}{k}\)
我怎么才想起来我在情侣那个题用过这个
然后直接找指数为 \(m-n\) 的项。
\(=\sum\limits_{j=0}^{\infty} f(j) \dbinom{m-n-a(j)+2n-1}{m-n-a(j)}\)
这个就可以做啦。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号