洛谷算法题
数字反转
https://www.luogu.com.cn/problem/P5705?contestId=152153
浮点数的使用
通过atoi函数可以把字符串转化为相对应的数字

需要注意的是,本题输入的浮点数在实际解题中会出现有效值的问题
如:
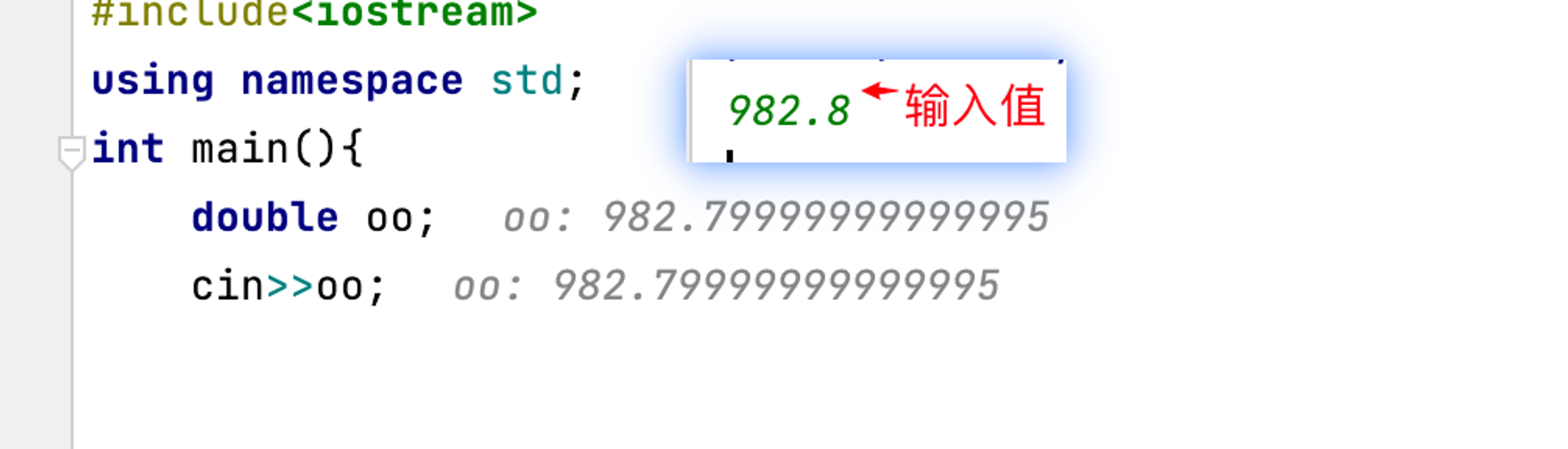
题解:https://www.luogu.com.cn/problem/solution/P5705(题解里有此问题的许多不同解,可以学习)
迪杰斯特拉算法
模板题:
https://www.luogu.com.cn/problem/P4779
最短路径问题可以用迪杰斯特拉算法,算法可以套用模版,将代码背诵下来直接写
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1000;
#define INF 1000000001
int n,m;
int s;
int g[N][N]; //记录边
int len[N+1]; //从顶点到端点的长度
bool st[N+1]; //是否已访问点
void dijkstra(){
for(int i=1;i<=n;i++) {
st[i] = false;
len[i] = INF;
}
st[s] = true;
len[s] = 0;
for(int i=0;i<n;i++){
int id = s,mind = INF;
for(int j=1;j<=n;j++){ //找到最短路径
if (!st[j]&&len[j]<mind){
mind = len[j];
id = j;
}
}
st[id] = true;
for(int k=1;k<=n;k++){ //修改路径长度
len[k] = min(len[k], len[id] + g[id][k]);
}
}
}
int main() {
cin>>n>>m>>s;
int ui,vi,wi;
for(int i=0;i<=n;i++){
for(int j=0;j<=n;j++){
g[i][j] = INF;
}
}
for(int i=0;i<m;i++){
cin>>ui>>vi>>wi;
g[ui][vi] = min(wi, g[ui][vi]) ;
}
dijkstra();
for(int i=1;i<=n;i++){
cout<<len[i]<<" ";
}
}
背包问题
背包问题的求解通常使用动态规划方法。动态规划是一种将复杂问题分解为更简单子问题的方式。在背包问题中,动态规划可以用来计算每个可能的背包重量下的最大价值。
动态规划解决0-1背包问题的步骤如下:
- 定义一个二维数组dp[i][j],其中i表示可选的物品,j表示背包的容量。
- 初始化dp数组,当没有物品或者背包容量为0时,dp[i][j]均为0。
- 对于每种物品i和每个背包容量j,我们需要判断当前物品i是否可以放入背包中:
- 如果当前物品i的重量大于背包容量j,则无法放入,此时dp[i][j] = dp[i-1][j]。
- 否则,可以考虑放入当前物品i或者不放入,取两者的最大值,即dp[i][j] = max(dp[i-1][j], dp[i-1][j-物品i的重量] + 物品i的价值)。
- 最终,dp[n][m]即为问题的解,其中n表示物品的种类数,m表示背包的容量。
// <https://kamacoder.com/problempage.php?pid=1046>
#include<iostream>
#include<vector>
using namespace std;
int main(){
vector<int> weight ;
vector<int> value;
int M,N;
cin>>M>>N;
int t;
for(int i=0;i<M;i++){
cin>>t;
weight.push_back(t);
}
for(int i=0;i<M;i++){
cin>>t;
value.push_back(t);
}
// vector<vector<int>> dp(M,vector<int>(N+1,0));
vector< vector<int> > dp(weight.size(), vector<int>(N + 1, 0));
for(int i=weight[0];i<=N;i++){
dp[0][i] = value[0];
}
for(int i=1;i<M;i++){
for(int j=1;j<=N;j++){
if(j<weight[i]) dp[i][j] = dp[i-1][j];
else{
dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
}
}
}
cout<<dp[M-1][N];
}
相关博客:
🔺https://github.com/youngyangyang04/leetcode-master/blob/master/problems/背包理论基础01背包-1.md
字符串排序
https://www.luogu.com.cn/problem/P1308?contestId=152172
模拟题
知识点: find函数应用,大小写转换
#include <iostream>
#include <string>
#include <algorithm>
const int MAX = 1001;
using namespace std;
int main(){
string s;
string A[MAX];
int i=0;//记录数组位置
string t;
getline(cin,s); //待查字符串
getline(cin,t);
int pos = 0;
//将字符串全部变为小写
transform(s.begin(),s.end(),s.begin(),::towlower);
transform(t.begin(),t.end(),t.begin(),::towlower);
t =' '+t+' ';
s=' '+s+' ';
if (t.find(s)==string::npos){
cout<<-1;
return 0;
} else{
pos = t.find(s);
}
int acc = 0;
int end = t.find(s);
while (end!=string::npos){
acc++;
end = t.find(s,end+1);
}
cout<<acc<<" "<<pos;
// for (int j = 0; j < size; ++j) {
//// if (j==0){//开始和结束时单独考虑
////
//// }
// if (t.at(j)==' ') {
// if (flag==1) {
// end = j;
// A[i++] = t.substr(begin+1,end-begin-1);//后面的为切割字符串的长度
//// flag = 0 ;
// begin=j;
// } else{
// flag = 1;
// begin = j;
// }
// }
//// }
// bool f = false;
// int acc = 0;
//
// for (int j = 0; j < i; ++j) {
//// transform(A[j].begin(),A[j].end(),A[j].begin(),::towlower);
//
// if (s==A[j]&&!f)
// { //首次碰到
// f = true;
// acc++;
// //计算首次出现的位置
//
//
// } else if (s == A[j]&&f){
// acc++;
// }
// }
// if (f){
// cout<<acc<<" "<<pos;
// } else{
// cout<<-1;
// }
return 0;
}
P1192 台阶问题
知识点: 递推,斐波那契数列,递推转非递推
递推方法会导致Time Limit Exceeded
#include <iostream>
using namespace std;
int times = 0;
int N,K;
void Fib(int stepLen,int n,int target){
int then = n+stepLen;
if (n+stepLen>target) return;
else if (n+stepLen==target)times++;
else{ //还没到目标台阶
for (int i = 1; i <=K; ++i) {
Fib(i,then,N);
}
}
}
int main(){
cin>>N>>K;
Fib(0,0,N);
cout<<times%100003;
}
非递推(dp):
#include <iostream>
using namespace std;
const int MAXN = 1000001;
int A[MAXN];
int N,K;
int main(){
cin>>N>>K;
A[0] = 1;
A[1] = 1;
for (int i = 2; i <=N ; ++i) {
for (int j = 1; j<=K&&j<=i; ++j) {
A[i] =(A[i] +A[i-j])%100003 ;
}
}
cout<<A[N];
}
记住边计算边取模
P1111 修复公路
知识点:并查集的使用
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1002;
const int MAXM = 100003;
struct Node{
int x;
int y;
int t;
}node[MAXM];
int N,M;
int tree[MAXN];
int findFather(int a){
if (a== tree[a])return a;
else{
return findFather(tree[a]);
}
}
bool compare(Node a,Node b){
return a.t<b.t;
}
int main(){
int x,y,t;
cin>>N>>M; //N为村庄数,M为道路数
for (int i = 1; i <= N; ++i) {//初始化
tree[i] = i;
}
for (int i = 1; i <= M; ++i) {
cin>>x>>y>>t;
if (x>y) swap(x,y);
node[i].x = x;
node[i].y = y;
node[i].t = t;
}
sort(node+1,node+M+1, compare);
int num = 0;
int ans = 0;
for (int i = 1; i <= M; ++i) {
if (findFather(node[i].x)!= findFather(node[i].y)){//若祖先不同则进行合并
num++;
tree[findFather(node[i].y)] = findFather(node[i].x);
ans = node[i].t;
}
}
if (num == N-1) cout<<ans;
else cout<<-1;
}
并查集的使用中,这一步很关键

炸铁路问题
知识点:并查集,Tarjan算法
https://www.luogu.com.cn/problem/P1656
我首先使用并查集暴力求解 ,样例通过但是提交之后全部WA
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int MAXCity=151;
int n,m;
int City[MAXCity];
int City2[MAXCity];
struct Edge{
int x;
int y;
}edge[5001];
bool compare(Edge a,Edge b){
if (a.x==b.x) return a.y<b.y;
else return a.x<b.x;
}
int findFather(int t){
if (City[t]==t) return t;
else return findFather(City[t]);
}
bool isConnect(int x){//去掉第x行
int ans = 0;
for (int i = 1; i <= m ; ++i) {
if (i==x) continue;
int a = City2[edge[i].x];
int b = City2[edge[i].y];
if (a!=b){
City2[edge[i].y] = findFather(a);
ans++;
}
}
if (ans==n-1) return true;
else return false;
}
int main(){
cin>>n>>m;
for (int i = 1; i <=m; ++i) {
cin>>edge[i].x>>edge[i].y;
}
sort(edge+1,edge+m+1,compare);
for (int i = 1; i <=n ; ++i) {
City[i] = i;
}
vector<int> result;
for (int i = 1; i <=n ; ++i){
for (int j = 1; j <=n ; ++j) {
City2[j] = City[j];
}
if (!isConnect(i)) result.push_back(i);
}
for (int i = 0; i < result.size(); ++i) {
int a1 = edge[result[i]].x;
int a2 = edge[result[i]].y;
cout<<a1<<" "<<a2;
if (i!=result.size()-1) cout<<endl;
}
}
后来发现在红框处添加 if (edge[i].x>edge[i].y) swap(edge[i].y,edge[i].x);

结果通过了三个样例
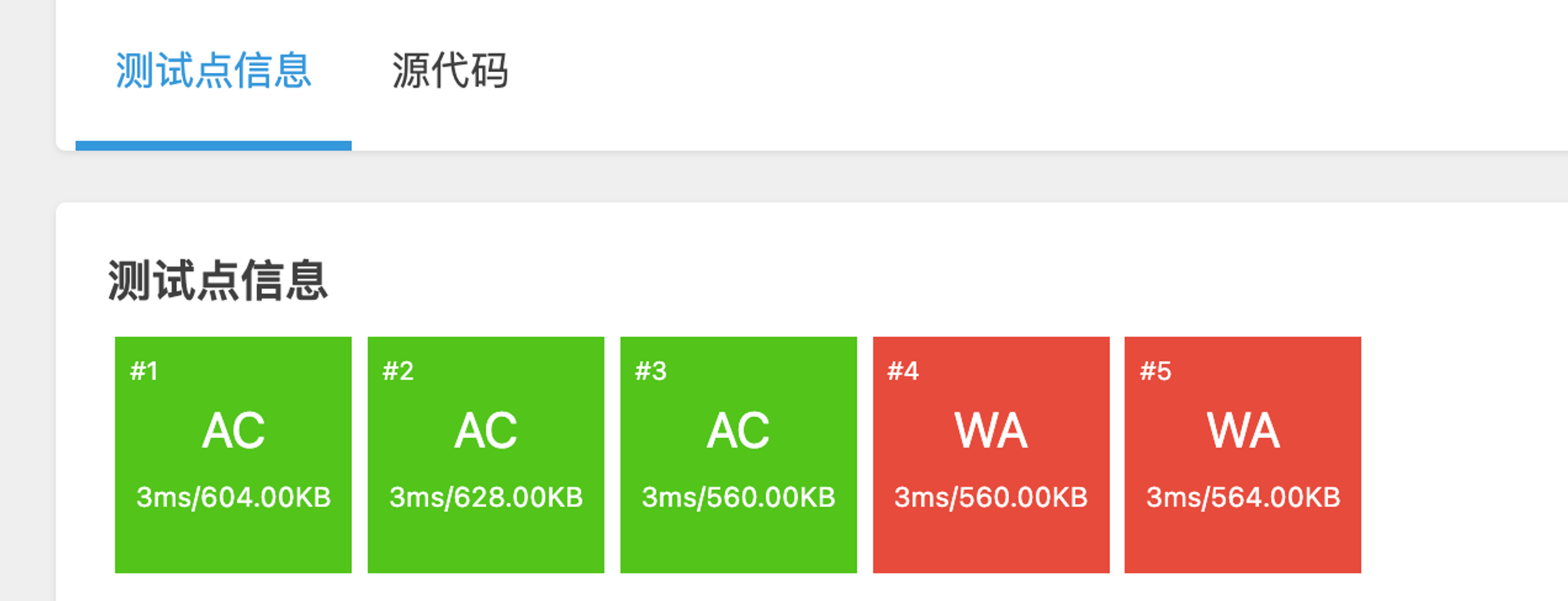
参考:
Tarjan算法:求解图的割点与桥(割边) - nullzx - 博客园
计数问题
#include <iostream>
#include <algorithm>
using namespace std;
int main(){
int n;
char x;
cin>>n>>x;
int ans = 0;
for (int i = 1; i <= n; ++i) {
string r = to_string(i);
if (r.find(x)!=string::npos){
ans+= count(r.begin(), r.end(),x);
}
}
cout<<ans;
return 0;
}
🍎八皇后问题
[USACO1.5] 八皇后 Checker Challenge - 洛谷
知识点: DFS
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <cmath>
#define MAXN 40
using namespace std;
int n;
/*
* 0行用来记录列
* 1行记录主对角线平行方向的状态
* 2行用来记录副对角线状态
*/
bool diag[MAXN][MAXN]; //用来记录状态
int ans[MAXN];
int sum = 0;
void queen(int line){ //line为行号
if (line>n){
sum++;
if (sum>3) return;
else{
for (int i = 1; i <= n; ++i) {
cout<<ans[i]<<" ";
}
cout<<endl;
}
}
for (int i = 1; i <= n; ++i) {
if (!diag[0][i]&&!diag[1][line+i]&&!diag[2][i-line+n]){
ans[line] = i;
diag[0][i] = true;
diag[1][line+i] = true;
diag[2][i-line+n] = true;
queen(line+1);
diag[0][i] = false;
diag[1][line+i] = false;
diag[2][i-line+n] = false;
}
}
}
int main(){
cin>>n;
//初始化数组
for (int i = 0; i < MAXN; ++i) {
for (int j = 0; j < MAXN; ++j) {
diag[i][j] = false;
}
}
queen(1);
cout<<sum;
}
注意数组应开大一点,因为斜向会导致数组下标增大。
P3375 【模板】KMP
暴力求解代码:
//
// Created by CrisKey on 2024/2/27.
//
#include <iostream>
using namespace std;
#define MAXN 1003
int kmp[MAXN];
//void cal_kmp(string s,int kmp[]){
// int len = s.length();
// int j = -1;
//
// for (int i = 1; i < len; ++i) {
// while(j==-1||)
// }
//
//
//}
int main(){
string s1,s2;
cin>>s1>>s2;
int begin = 0;
int len1 = s1.length();
int len2 = s2.length();
int j = 0;
for (int i = 0; i < len1; ++i) {
if (s1[i]==s2[j]) j++;
else{
j=0;
i= begin;
begin = begin+1;
}
if (j==len2){
cout<<begin+1<<endl;
i=begin;
begin = begin+1;
j=0;
}
}
cout<<0<<" ";
int max = 0;
for (int j = 1; j < len2; ++j) {
int m = 0;
int n = 1;
int begin = n;
while(n<=j){
if (s2[m]==s2[n]){
m++;
n++;
} else{
m=0;
n=begin+1;
begin++;
}
}
if (m>max)max = m;
cout<<max<<" ";
max = 0;
}
}
参考:
设置精度可以使用:
cout << setprecision(20)<<sum+1; *//设置精度同时需加入头文件:
#include**<iomanip>
本文来自博客园,作者:我只有一天的回忆,转载请注明原文链接:https://www.cnblogs.com/cc-coding/p/18315318


 浙公网安备 33010602011771号
浙公网安备 33010602011771号