算法学习（算法笔记胡凡）

目录

• 考生排序
• 递归问题
  • 数塔问题
  • 回文字符串
  • 棋盘覆盖问题
  • 盒分形
  • 自然数分解之最大积
  • 自然数分解之方案数
  • 01串
• STL练习
  • 迭代器的使用

考生排序

https://sunnywhy.com/sfbj/4/1/92

结构体的使用,sort函数的使用

递归问题

数塔问题

https://sunnywhy.com/sfbj/4/3/116

动态规划问题dp

例如给定样例

5
5
8 3
12 7 16
4 10 11 6
9 5 3 9 4

方程:

dp[n][j]= s[n][j] 最后一排作为塔顶时，其最大值即为其自身值

dp[i][j] = max(dp[i+1][j],dp[i+1][j+1])+s[i][j] 非最后一排，其最大值为其相连左下角和右下角作为塔顶的最大值加上其自身值

参考：

• https://blog.csdn.net/i6223671/article/details/89788714

回文字符串

https://sunnywhy.com/sfbj/4/3/117

使用递归求解，考虑如何将其划分为小问题

棋盘覆盖问题

https://sunnywhy.com/sfbj/4/3/120

分治法

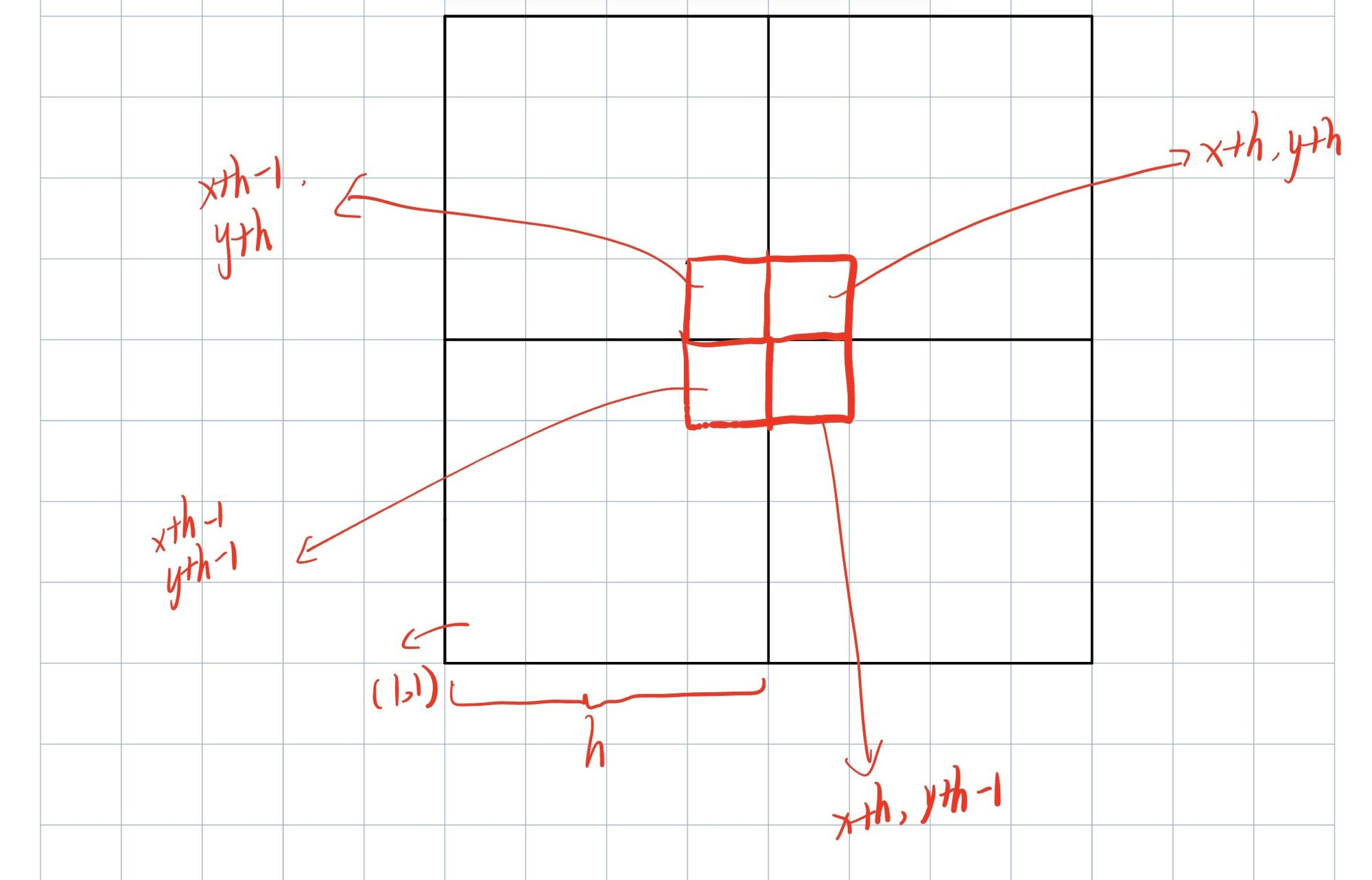
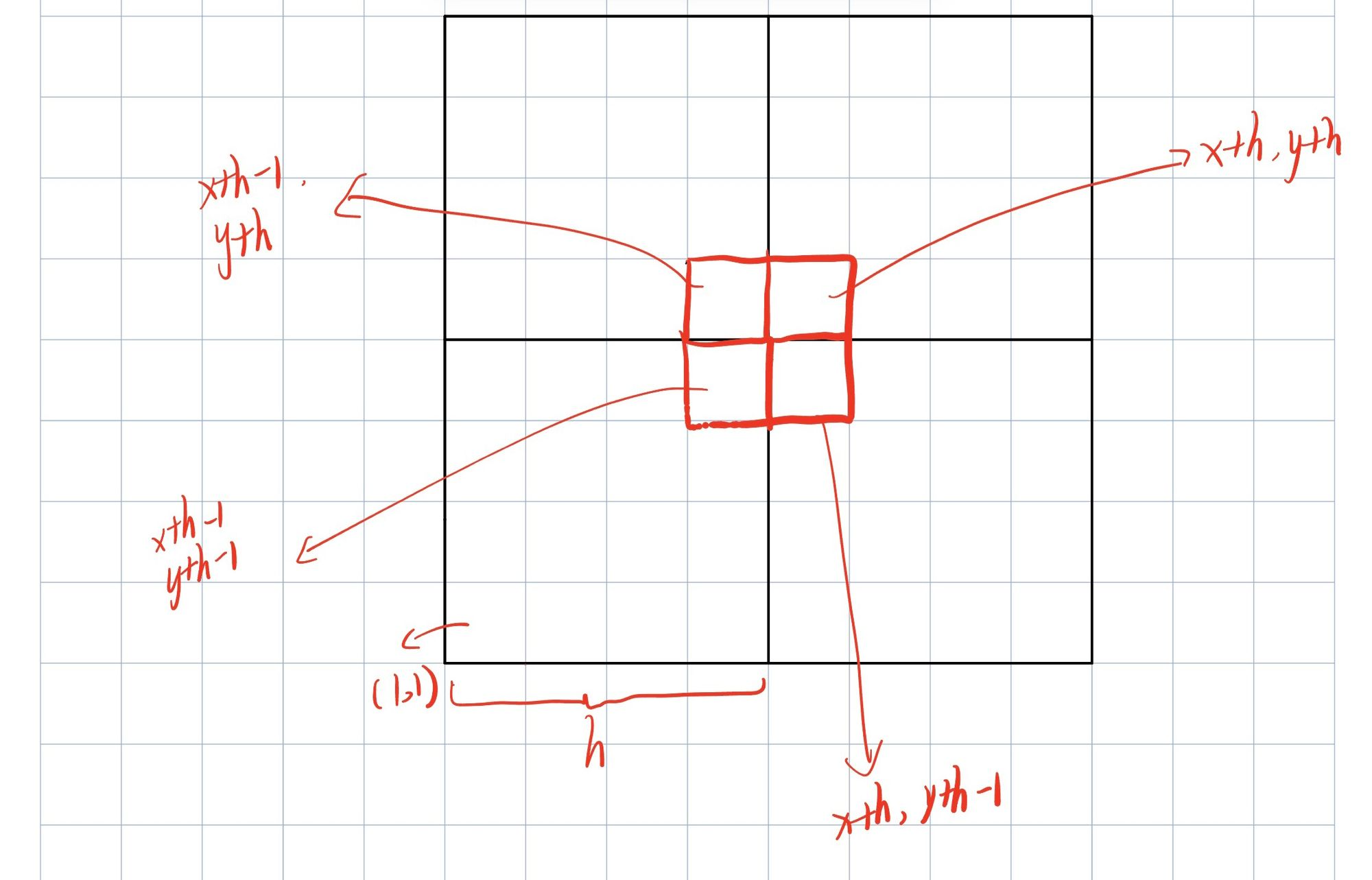
使用分治的思想，将大棋盘划分为四个小棋盘，特殊格必位于四个小棋盘中的一个，假设位于左上子棋盘，则将左上子棋盘与其他子棋盘联通处，使用一个L型骨牌将其他三个无特殊格的子棋盘变为有特殊格，此时问题便转化为了四个规模较小的子问题。

即步骤为：

1. 将大棋盘划分为四个小棋盘，特殊格必位于四个小棋盘中的一个。
2. 假设特殊格位于左上子棋盘，在左上子棋盘与其他子棋盘联通处，使用一个L型骨牌将其他三个无特殊格的子棋盘变为有特殊格。
3. 这样，问题便转化为了四个规模较小的子问题，对四个子棋盘重复上述步骤，直到棋盘不能再划分。

具体函数编写：

首先判断是否在左上，若在左上，则在联通处使用L型骨牌，并递归进入左上子棋盘，若不在左上，则将左上子棋盘的右下角设为特殊格并递归进入左上子棋盘。其他子棋盘同理。

代码+注释：

#include<iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
#define MAXN (256*256-1)/3

int i=0;//使用的L型骨牌数目

struct Point{
    int x,y;
    Point(){}
    Point(int _x,int _y){
        x=_x;
        y=_y;
    }
}cards[MAXN];

bool cmp(Point a, Point b) {
    if (a.x != b.x) return a.x < b.x;
    else return a.y < b.y;
}

void chessBoard(int x,int y,int cx,int cy,int k);

int main(){
    int k,cx,cy;
    cin>>k>>cx>>cy;
    int h = (int)pow(2.0,1.0*k);
    chessBoard(1,1,cx,cy,h);
   
    sort(cards,cards+i,cmp);
    for (int j= 0; j < i; j++)
    {
     cout<<cards[j].x<<" "<<cards[j].y<<endl;

     
    }

}
void chessBoard(int x,int y,int cx,int cy,int k){ //x,y为当前求解的棋盘的左下角的点
    if (k==1) return;
    int h = k/2; //h代表将棋盘分为四个，一个正方形子棋盘的长与宽
    //首先考虑特殊点在子棋盘的左上角
    if (cx<x+h&&cy>=y+h) {
        cards[i++] =Point(x+h,y+h-1); //cards用来记录使用过的L型骨牌
        chessBoard(x,y+h,cx,cy,h);//递归进入子棋盘
    }else{//若不在左上角
        chessBoard(x,y+h,x+h-1,y+h,h);//若特殊点不在左上棋盘，则填充左上棋盘中的右下角
    }
    //左下
    if (cx<x+h&&cy<y+h){
        cards[i++] = Point(x+h,y+h);
        chessBoard(x,y,cx,cy,h);
    } else{
        chessBoard(x,y,x+h-1,y+h-1,h);
    }
    //右上
     if (cx>=x+h&&cy>=y+h){
        cards[i++] = Point(x+h-1,y+h-1);
        chessBoard(x+h,y+h,cx,cy,h);
    } else{
        chessBoard(x+h,y+h,x+h,y+h,h);
    }
     //右下
    if (cx>=x+h&&cy<y+h)
    {
      cards[i++] = Point(x+h-1,y+h);
      chessBoard(x+h,y,cx,cy,h);
    }else{
      chessBoard(x+h,y,x+h,y+h-1,h);
    }

}

参考：

• https://blog.csdn.net/SongXJ_01/article/details/112439322
• https://sunnywhy.com/sfbj/4/3/120题解

盒分形

https://sunnywhy.com/sfbj/4/3

首先确定问题规模,n层的盒分形问题规模为 \(3^{n-1}\),即n度的盒分形图为一个长宽为 \(3^{n-1}\)的正方形。

#include<iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
#include <cstring>
using namespace std;
const int  MAXN =2187;

char point[MAXN][MAXN];

void printBox(int x,int y,int n);

void printBox(int x,int y,int n){
    if (n==1) point[x][y] = 'X';
    else{
      int d = (int)(pow(3.0,n-2));
        printBox(x,y,n-1);
        printBox(x,y+2*d,n-1);
        printBox(x+d,y+d,n-1);
        printBox(x+2*d,y,n-1);
        printBox(x+2*d,y+2*d,n-1);
    }
}

int main(){
  int n;
  cin>>n;
  int unit = (int)pow(3.0,n-1);//矩形的长和宽
  for (int i = 0; i < unit; i++)
  {
    for(int j=0;j<unit;j++){
      point[i][j]=' ';
    }
  }
  printBox(0,0,n);
  for (int i = 0; i < unit; i++)
  {
    for(int j=0;j<unit;j++){
      cout<<point[i][j];
    }
    cout<<endl;
  }
  

}

参考：

• https://blog.csdn.net/a253664942/article/details/45566889

自然数分解之最大积

https://sunnywhy.com/sfbj/4/3/124

当n≥4时：

通过观察规律4=2+2,5=2+3,6=3+3,7=3+2+2…

可以发现拆分的自然数不超过3（拆成1对乘积没有贡献，不如加到后面的数中）且2*3>5,则所有的数只能拆成2或者3

用动态规划求解：

分析n≥4的情况，因为当n<4时，最大乘积为其自身。而本题要求至少分为两个正整数的乘积，则n=2,3的情况与后面不同，单独考虑。

#include<iostream>
using namespace std;
int F(int k){
  if (k==1||k==2||k==3)
  {
    return k;
  }

  // int max = k;
  int max = 1*F(k-1);
  for (int i = 2; i < k; i++)
  {
    if((i*F(k-i))>max){
      max=i*F(k-i);
    }
  }
  return max;
}

int main(){
  int n;
  cin>>n;
  if (n==2)
  {
    cout<<1;
  }else if(n==3){cout<<2;}
  else
  cout<<F(n);
}

自然数分解之方案数

https://sunnywhy.com/sfbj/4/3/125

参考：

• https://blog.csdn.net/weixin_37577134/article/details/102597579

01串

https://sunnywhy.com/sfbj/4/3/128/solution

STL练习

迭代器的使用

要访问顺序容器或者关联容器，可以使用迭代器iterator,迭代器可以指向容器中的某个元素，通过迭代器就可以读写它指向的元素。从这一点上看，迭代器和指针类似。

vector<int>::iterator   it;    //定义一个名为it的变量

cout<<*it;      //输出it所指元素
it++;