模拟赛 0915/0916
Day1
T1
\(Idea\)
题目链接
看到这题就想起\(CRT\)。看到\(m_i\)不互质,想到\(EXCRT\);
于是枚举\(a_i\),复杂度为\(O(n\prod m_i),60\;pts\)
正解
令\(Lcm=lcm\{m\}\),则对于任意的\(x\),\(x \bmod \{m\}\)得到的\(\{a\}\)总是与
\(x+Lcm \bmod \{m\}\)得到的\(\{a\}\)是相同的。对于任意\(x,y(x \not = y)\),若它们的差不超过\(Lcm\),
那么说明它们至少在模一个\(m_i\)时不同,即存在不同的\(\{a\}\)
所以对于\(\{m\}\)来说,如果保证\(m_i\)互不相同,那么恰好存在\(Lcm\)个\(x\) 存在\(\{a\}\) 互不相同
即\(ans=\prod m-Lcm\) ;复杂度\(O(n)\)
\(Code\)
inline int gcd(int a,int b){
if(b==0) return a;
return gcd(b,a%b);
}
signed main(){
//freopen(File".in","r",stdin);
//freopen(File".out","w",stdout);
int n=read();
int ans=1,lcm=1;
for(int i=1;i<=n;i++){
int v=read();
ans*=v; lcm=lcm/gcd(v,lcm)*v;
}
printf("%lld",ans-lcm);
return 0;
}
T2
\(\text{题意}\)
给定一棵 \(n\) 个节点的树,树上第 \(i\) 个点的权值为 \(a_i \in \{0,1\}\)。对于每个节点询问最大联
通块的大小,使得该联通块包含该节点,同时含有偶数个 \(a_i=0\)的节点。
\(Idea\)
题目链接
由于要记录整个树的所有点答案就不能从一个点的最近0处考虑,那么现在们来考虑一下,在一个权值为0的点处,
答案就可能在它的子树内部和子树的外部进行取\(max\),也可能是他的子树内外都有,是对于总答案的贡献,这样的话,我们就开两个数组:\(up[]\),\(dw[]\)。这是用来记录这个点子树之外的贡献和这个点子树的贡献。在\(dfs\)求每个子树大小的时候就可以更新好这两个数组的初值。
接下来就是标记的上下传递了,这里要从上到下,从下到上进行统计,在向上统计的时候还比较麻烦,要对于对应点的一个区间进行边界更新处理,这样保证内外子树的答案的合法性。
\(Code\)
给出\(blng\)的\(Code\),对于学长\(Cydiater\)的\(C++11\;’std\)看不懂
#include<bits/stdc++.h>
using namespace std;
inline int read(){int r;int s=0,c;for(;!isdigit(c=getchar());s=c);for(r=c^48;isdigit(c=getchar());(r*=10)+=c^48);return s^45?r:-r;}
const int sea=1e6+7;
int n,tot,a[sea],up[sea],dw[sea],ans[sea],size[sea];
vector<int>v[sea];
template<typename T> inline bool cmax(T &a, T b) {return a < b ? a = b, 1 : 0;}
void dfs(int x,int fa)
{
size[x]=1;
for(int i=0;i<v[x].size();i++)
{
int y=v[x][i];if(y==fa) continue;
dfs(y,x); size[x]+=size[y];
}
if(a[x]==0)
{
for(int i=0;i<v[x].size();i++)
{
int y=v[x][i];if(y==fa) continue;
cmax(dw[y],size[y]);
}
cmax(up[x],n-size[x]);
}//初值统计
}
void dfs_up(int x,int fa)
{
for(int i=0;i<v[x].size();i++)
{
int y=v[x][i];if(y==fa) continue;
dfs_up(y,x); cmax(up[x],up[y]),cmax(ans[x],up[y]);
}//用up[y]来更新up[x]和ans[x],这整个操作是自底向上的,所以是向上传递标记
int p=0,q=0;
//这里也可以理解成一个区间,p是在正向更新向上更新时的最下面的值,q是在逆向更新向上更新时的最下面的值
for(int i=0;i<v[x].size();i++)
{
int y=v[x][i];if(y==fa) continue;
cmax(dw[y],p),cmax(p,up[y]);//用p更新y的子树内的贡献,然后用子树外的贡献去更新p,达到一种边界处理的效果
}
reverse(v[x].begin(),v[x].end());//这里就是逆序了,倒序的操作,自行百度吧
//提醒一下这里还是用vector吧,结构体真的不好写,,
for(int i=0;i<v[x].size();i++)
{
int y=v[x][i];if(y==fa) continue;
cmax(dw[y],q),cmax(q,up[y]);
}
}
void dfs_dw(int x,int fa)
{
cmax(ans[x],dw[x]);
for(int i=0;i<v[x].size();i++)
{
int y=v[x][i];if(y==fa) continue;
cmax(dw[y],dw[x]);dfs_dw(y,x);
}
}//用dw[x]来更新ans[x]和dw[y],这整个操作是自上向底的,所以是向下传递标记
int main()
{
n=read(); for(int i=1;i<=n;i++) a[i]=read();
for(int i=2;i<=n;i++)
{
int x=read(),y=read();
v[x].push_back(y),v[y].push_back(x);
}
for(int i=1;i<=n;i++) tot+=(a[i]==0);
if(tot%2==0){for(int i=1;i<=n;i++) printf("%d\n",n);return 0;}
dfs(1,0); dfs_up(1,0); dfs_dw(1,0);
for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
return 0;
}
给出另外一种写法点我( • ̀ω•́ )✧
T3
\(\text{题意}\) :连续区间取模的总和
\(Idea\)
题目链接
\(\text{当然可以n^3暴力}\)
先说学长的算法:
1.主席树 复杂度\(O(n log^2 n)\)
当固定左端点时,查询右端点本质上是在下标后缀内对权值进行区间取最小值,
可以利用主席树来解决
2.线段树/BIT 复杂度\(O(n log^2 n)\)
可以考虑只拿线段树来维护,但是具体实现时会发现这个线段树更新的顺序和我们询
问的顺序是相反的,同时因为\(max\) 自己的性质并不好直接修改。
可以通过维护每个权值的下一个出现位置来实现更新;
另外还有一种处理方法,观察到插入和询问恰好是逆序关系,因此我们记录下修改的
过程,在询问时倒退撤销之前的修改操作即可,这种做法对空间的消耗可能比较大。
3.二分\(+RMQ\) 复杂度\(O(n log^2 n)\)
可以发现本题中每次的查找具有可二分性,每次查找二分即可。
注意判定时需要用 \(ST\)表来维护 \(RMQ\)。
4.分治[标算] 重新审视这个题目,可以发现我们查找的过程其实很符合序列分治的结构。。。
本cb只会用线段树,同时参考了这篇( • ̀ω•́ )✧<同上的链接>
\(Code\)
struct Node{
int l,r,w;
}tree[maxn<<2];
int n,ans,sum,a[maxn];
inline void build(int k,int l,int r){
tree[k].l=l,tree[k].r=r;
if(l==r){tree[k].w=a[l];return ;}
int mid=l+r>>1;
build(lk,l,mid);build(rk,mid+1,r);
tree[k].w=min(tree[lk].w,tree[rk].w);
}
inline void init(int k,int x){
int l=tree[k].l,r=tree[k].r;
if(l==r){tree[k].w=inf;return ;}
int mid=l+r>>1;
if(x<=mid) init(lk,x);
else init(rk,x);
tree[k].w=min(tree[lk].w,tree[rk].w);
}
inline int ask(int k,int x){
int l=tree[k].l,r=tree[k].r;
if(l==r) return l;
if(tree[k].w>x) return n+1;
if(tree[lk].w<=x) return ask(lk,x);
return ask(rk,x);
}
signed main(){
n=read();
for(int i=1;i<=n;i++) a[i]=read();
build(1,1,n);
for(int i=1;i<=n;i++){
init(1,i);
int j=i+1;int last=a[i];ans+=a[i];
while(j<=n){
int w=ask(1,last); ans+=(w-j)*last;
if(w<=n) last=last%a[w]; j=w;
}
}
printf("%lld",ans);
return 0;
}
Day2
T1
\(\text{题意}\) 给你一张无向图,找到使\(\left|cnt(x)-cnt(y)\right|\)最大的联通子图。求最大的 \(\left|cnt(x)-cnt(y)\right|\)
\(Idea\)
题目链接
这题可以白嫖\(35pts\)
\({Code}_1\)
\(dfs\)即可
bool flag=1;
int a[maxn],l[maxn],r[maxn];
bool vis[maxn];
struct edge{
int v,next;
}e[maxn<<1];
int head[maxn];
int tot;
inline void add(int x,int y){
e[++tot].v=y; e[tot].next=head[x];
head[x]=tot;
}
inline void dfs(int u){
vis[u]=true;
l[u]=a[u], r[u]=-a[u];
for(int i=head[u];i;i=e[i].next){
int y=e[i].v;
if(vis[y])continue;
dfs(y);
if(r[y]>0) r[u]+=r[y];
if(l[y]>0) l[u]+=l[y];
}
return ;
}
signed main(){
freopen(File".in","r",stdin);
freopen(File".out","w",stdout);
n=read();
for(int i=1;i<=n;i++){
a[i]=read();
if(a[i]==0) a[i]=1;
else a[i]=-1;
if(i>=2) if(a[i]!=a[i-1])
flag=0;
}
if(flag) return printf("%d",n),0;
else{
for(int i=1;i<n;i++){
int x=read(),y=read();
add(x,y); add(y,x);
}
dfs(1);
int ans=0;
for(int i=1;i<=n;i++){
int s=max(l[i],r[i]);
ans=max(ans,s);
}
printf("%d",ans);
}
return 0;
}
\({Code}_2\)
\(blng\)的\(\text{树形DP}\)

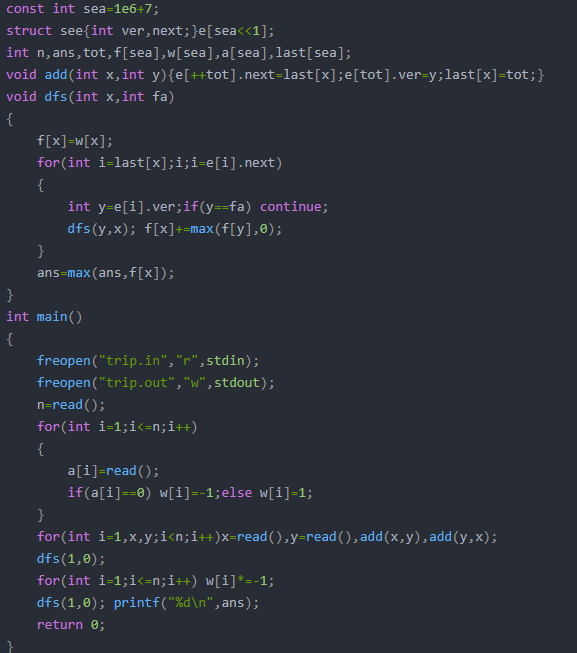
给你们看眼,这就是强者;\(\%\%blng\)
菜鸡
T2
\(\text{给你一个长度len,一个字符集s,让你随意放字符,保证放出来的串是回文的而且任意位的前缀不为回文,求方案数}\)
\(Idea\)
题目链接
这题打表,只写了\(n \le 5\)的 相信大佬们能推出来 [呲牙]
题解




好的上代码
\(Code_1\)
const int mod = 1e9 + 7;
inline int add(int a, int b) {a += b; return a >= mod ? a - mod : a;}
inline int pop(int a, int b) {a -= b; return a < 0 ? a + mod : a;}
inline int mul(int a, int b) {return (ll)a * b % mod;}
const int maxn = 1e6 + 5;
int n, m, f[maxn], pw[maxn], g[maxn];
int main() {
scanf("%d%d", &n, &m);
pw[0] = 1;
up (i, 1, n) pw[i] = mul(pw[i - 1], m);
up (i, 1, n) {
f[i] = pop(pw[(i + 1) / 2], g[(i + 1) / 2]);
if (i > 1) g[i] = add(f[i], mul(g[i - 1], m));
}
printf("%d", f[n]);
return 0;
}
\(Code2\)
先知道:若一个非回文子串是一个待定串的前一半的话,这个待定串就一定合法;
然后我们考虑前\(\frac{n+1}{2}\)的情况,如果直接求合法情况,肯定不太好求;
所以我们求不合法的情况,前半段的总方案数为\(m^{\frac{n+1}{2}}\),我们以三个字符\((abc),m=3\)为例
比如我们确定第一个字符为\(a\),那么有
共\(2m-1\)种不合法情况,共\(m\)个字符,共\(m(2m-1)=2m^2-m\)种不合法情况;
如果这半段不合法,前提是前半段合法;
又发现\(f_3=f_4,f_5=f_6,f_6=f_7...\),则\(f_i=f_{i+1},i \bmod 2==1\)
int f[maxn],power[maxn];
signed main(){
int n=read(),m=read();
f[1]=m%mod; f[2]=m; power[0]=1;
for(int i=1;i<=n;i++){
power[i]=power[i-1]*m;
power[i]%=mod;
}
int sum=0;
f[3]=power[2]-f[2]; f[3]%=mod;
sum=f[2];
for(int i=4;i<=n;i++){
f[i]=power[(i+1)/2];
f[i]-=sum;
f[i]%=mod;
if(!(i&1)){
sum*=m; sum%=mod;
sum+=f[i/2+1]; sum%=mod;
}
}
if(f[n]<0) f[n]+=mod;
printf("%d",f[n]);
return 0;
}
此处\(\%\)\(startaidou\)、\(blng\)
T3
\(\text{题意}\):
给定一个长度为 \(n\) 的序列,第 \(i\) 个位置为$ a_i$,同时给定 \(m\)。每次一个位置上的数可以
吃到相邻的权值不超过 \(a_i+m\) 的值,对于每个数询问是否存在一种方案使得其可以存活。
\(Idea\)
题目链接
此题需要注意的是
对于第 \(i\) 个位置上的数来说,如果其是整体最大的,那么显然这个数可以留到最后。
那么对于其他的数而言,我们找到其左边和右边第一个比他大的数,那么显然这个区间内的数都会被吃掉。
这个时候,如果左边或者右边的数可以留到最后,
同时这个区间内的和加上 \(m\) 满足吃掉左右端点中的一个时的限制,我们也可以说这个数能
够留到最后。
\(Code\)
找左边第一个大,右边第一个大 这里使用双端队列
deque<int>q;
int n,m;
int cl[maxn],cr[maxn];//左的一个大于,右第一个大于
int a[maxn],flag[maxn],sum[maxn];//sum前缀和,flag判断此数是否能留下
inline int dfs(int x){
if(flag[x]!=-1) return flag[x];
if(cl[x]==0&&cr[x]==n+1) return flag[x]=1;//如果当前的数为数列最大值,肯定可以留下来
flag[x]=0; int s=sum[cr[x]-1]-sum[cl[x]]+m;//求x的值+m;
if(cl[x]>0&&s>=a[cl[x]]) flag[x]|=dfs(cl[x]);//吃左
if(flag[x]==0&&cr[x]<=n&&s>=a[cr[x]]) flag[x]|=dfs(cr[x]); //吃右
return flag[x];
}
signed main(){
// freopen(File".in","r",stdin);
// freopen(File".out","w",stdout);
n=read(); m=read();
for(int i=1;i<=n;i++){
a[i]=read();
sum[i]=sum[i-1]+a[i];
}
a[0]=a[n+1]=inf;
q.push_back(0);
for(int i=1;i<=n;i++){//找左边第一个大
while(q.size()&&a[i]>=a[q.back()]) q.pop_back();
cl[i]=q.back(); q.push_back(i);
}
q.clear(); q.push_back(n+1);
for(int i=n;i>=1;i--){//找右边第一个大
while(q.size()&&a[i]>a[q.back()]) q.pop_back();
cr[i]=q.back(); q.push_back(i);
}
memset(flag,-1,sizeof flag);
for(int i=1;i<=n;i++) if(dfs(i)) printf("%d ",i);
return 0;
}
这里感谢\(G-hsm\);
总结
以上出现的\(dalao\)都比我强,我就是个菜鸡....
打模拟赛的话,能拿的分一定要拿。能吃下,就吃下。
感谢\(G-hsm,chdy,blng,startaidou\)对本博文的贡献
\(\text{有跨越大山的精神,必然有横渡海洋的气概,有蓝天般纯净存在,必然有爱惜生命的存在}\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号