分形与混沌

其实当我开始写下这个标题的时候，脑子里是“混沌”的。分形、混沌，两个看似简单的词语却包含太多即使是数学家无法窥探的奥妙，这样的两个词语，却带给我无限的思考。

我们知道现实生活中大部分都不是有序、稳定、确定的，而是处于一种无序的、不稳定的、不平衡的随机状态。换句话说，我们是不可能准确的预测生活中下一刻会发生什么，就像我们常说的“缘分”。在这样的状态中会存在无数的非线性的过程。尽管我们生活在一个及其复杂的非线性系统中，但是在很多的研究中，我们并不会直接研究非线性系统，而是抽象出来一个线性的系统。很多的经典物理学和一些经济学的理论就是如此。那么有没有想过这样的非线性系统也是有一定的规律可循的呢？当然这里可能会很矛盾，非线性系统是无序，不确定的，为什么又会有规律可循呢？非线性系统当然是由规律的，只是即使我们知道了这个规律，我们也无法预测它长期的状态。一个非线性系统的简单例子，我们都应该知道单摆，它就是一个很简单的线性系统，它在什么时候到达什么样的位置是可以准确确定的。但是如果加一根线，下面在连上一个球，它就变成了双摆了，也就是一个非线性系统的例子。

 

 

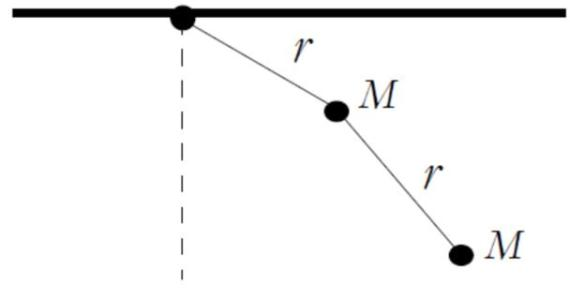
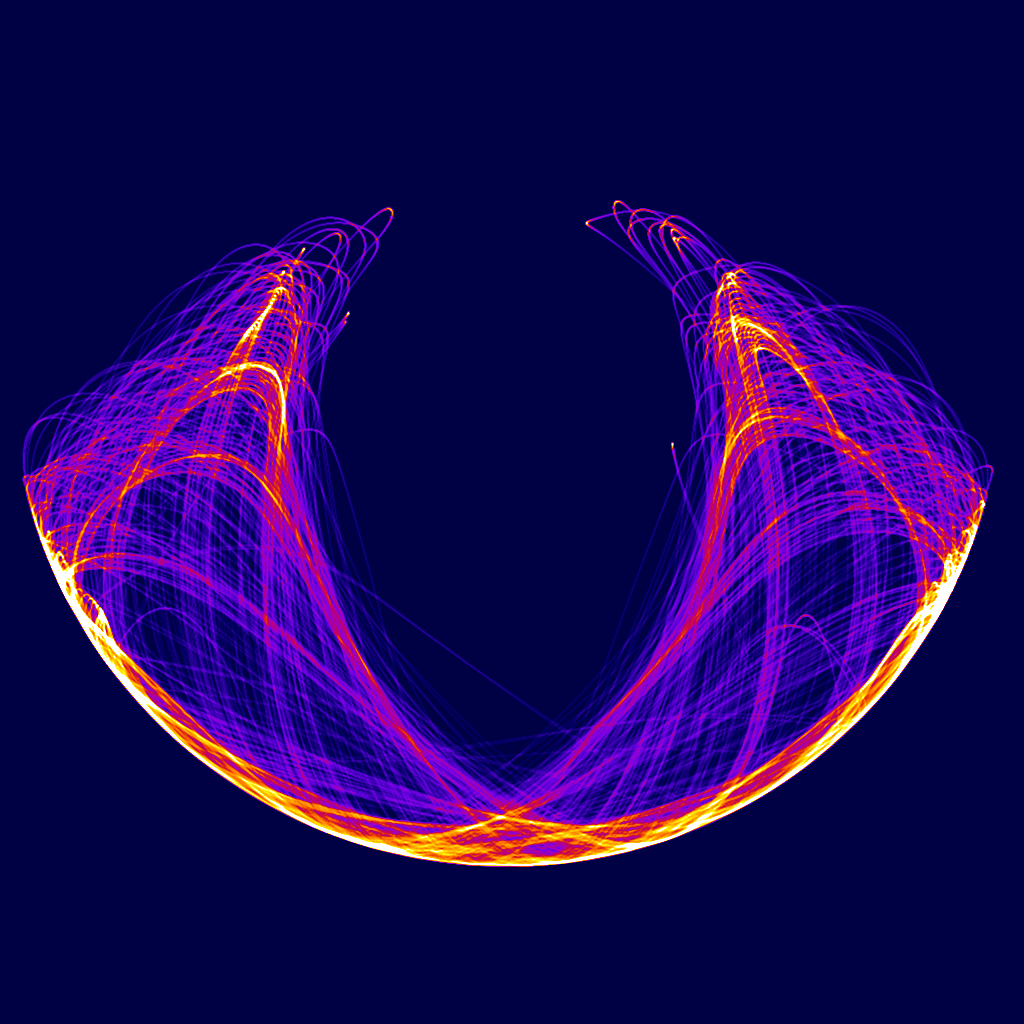
双摆的轨迹集合非常漂亮，这个双摆毫无疑问是有规律的，但是却无法确定它下一次的摆动位置，这就是非线性系统。它其实可以引申出混沌。

混沌是指发生在一个确定系统中的随机的不规则运动，换句话说在一个可以用数学或者是物理语言描述的确定系统中，却表现出了不会重复，不可预测的现象，这就是混沌。比如上面的双摆的例子，它的运动是可以使用物理公式来表达的，但是它的每次运动却都会产生一种看似随机的曲线，表现出混沌的性质。气象学家洛伦兹是混沌的开创者之一，他在计算天气模型的时候，因为一个偶然的事件（实际上是“偷了个懒”，把六位小数，输成了三位），结果发现自己的两个计算结果相差越来越大。这也是混沌的现象。也就是说混沌是对初值敏感的，初始值的任何一丁点改变都会对结果产生巨大的影响。英国演化生物学家、遗传学家瓦丁顿（Waddington）的胚胎发育坡模型（Epigenetic Landscape）能够很生动的解释这种现象，大家有心去可以自己去查一查。混沌也造成了我们熟知的几个现象：长期的天气注定无法预测，一个很小的扰动都会产生巨大的偏差；蝴蝶效应；非线性现象等等。

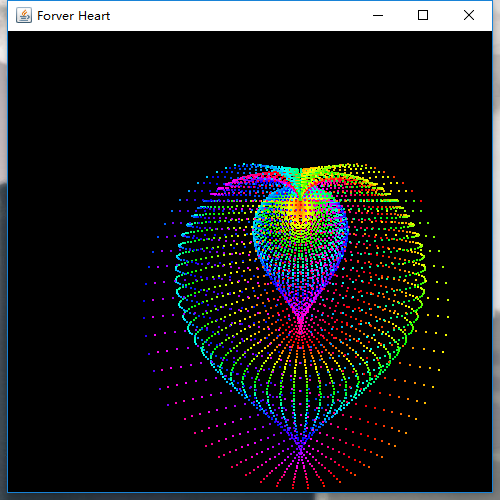
其实混沌是一个很有意思的东西，它可以给你带来很多意想不到的美丽。你可以找到很多不同的迭代公式，这些公式迭代都可能产生混沌的效应，然后利用手中的编程工具就能画出不一样的美丽。就比如这个：

代码也很简单：

package Heart;

import java.awt.Color;
import java.awt.Graphics;

import javax.swing.JFrame;

public class DrawHeart extends JFrame {

    public static void main(String[] args) {
        DrawHeart dh = new DrawHeart();
        dh.showUI();
    }

    // 初始化窗体界面
    public void showUI() {
        this.setTitle("Forver Heart");
        this.setSize(500, 500);
        this.getContentPane().setBackground(Color.BLACK);
        this.setDefaultCloseOperation(3);
        this.setLocationRelativeTo(null);
        this.setVisible(true);
    }

    public void paint(Graphics g) {
        super.paint(g);
                //迭代函数绘图
        for (int i = 0; i <= 180; i++) 
            for (int j = 0; j <= 180; j++) {
                double r = Math.PI / 45 * i * (1 - Math.sin(Math.PI / 45 * j))
                        * 20;
                double x = r * Math.cos(Math.PI / 45 * j)
                        * Math.sin(Math.PI / 45 * i) + 300;
                double y = -r * Math.sin(Math.PI / 45 * j) + 200;
                Color c = Color.getHSBColor(i * j / 8100.0f, 0.9999f, 0.9999f);
                g.setColor(c);
                g.drawOval((int) x, (int) y, 1, 1);
                try {
                    Thread.sleep(10);
                } catch (Exception e) {
                }
            }
    }
}

这个曲线有一个很美丽的名字——永恒之心。显然这个曲线表现出来了混沌的现象，它的公式是确定，在不断的迭代中改变了x和y的数值，这些数值又作为了新的参数继续迭代。在这样的迭代中产生看起来很随机的点，确定性和随机性的结合，构成了这样一幅美妙的图形。

前面我们说过，非线性系统其实也是有规律的，那么我们是否可以采取一些手段，透过复杂，混乱和不规则的形态来探寻他们背后的规律呢，为了解决这个问题分形理论应运而生。

分形最早是由Benoît B. Mandelbrot教授提出的，曼德尔布罗特也是分形学的专家之一。他有一个很经典的分形：曼德尔布罗特集合。

Mandelbrot集的妙处就在于如果你对它不断的放大，无论放大到多少倍，它又会呈现出一种类似的结构。这就是分形的一个很重要特征——自相似性，就是随便选取一个地方，不断的放大，放大之后呈现的又是原来的样子。其实自然现象中很多的事物都是复杂而没有规律的，比如云朵，浪花，树木，岩石。但是这些东西如果不断的放大之后又会发现，他们本身呈现出强烈的自相似。一棵树的结构其实和它的一根树枝很相像，然后一片树叶又和树的结构很像，甚至叶脉的结构也和整棵树一样。他们本身就可以看成是一种分形，自然界形成的分形。花菜是一种常见的东西，如果你用放大镜不断地去观察，你就会发现花菜的每一部分也都和整体的结构十分相似。

再举一例子——海岸线的长度。海岸线的长度到底有多长呢？有人可能会说那不是简单，直接去量不就好了。确实也是这么个道理，但是我们要注意一下的是该用什么样的尺度去量呢？假如在一个大尺度下去测量比如航拍，这样的尺度下很多海岸线的凸起是看不见的，整个海岸线会显得比较光滑，好这样测出一个长度。然后缩小一点尺度，让人步行去量，那么这时候，一些凸起就不能忽略了，然后由测出来一个长度。继续缩小尺度，我让一只蚂蚁去量，那么测出来的长度肯定要比前面的两种都长。也就是说，海岸线其实也是一种分形，他放大后会出现自相似的特性，放大的倍数越大，那么它就会越长，所以Mandelbrot教授提出了海岸线是无限长的理论。那么这个真的可以做到无限长吗？来看另一种分形：科赫曲线。

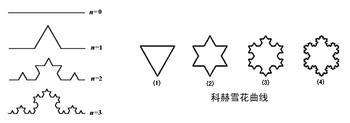
就像上图一样，在一段线段上取它中间的1/3然后做一个线段1/3长的等腰三角形，然后对新的线重复这个操作，就能得到科赫曲线。那么假设初始的线段长是1，一次迭代后它的长度就变成了4/3，再一次就变成了16/9；这样无限的迭代下去，它的长度就变成了4/3的n次方，当n趋于无穷大的时候，它的长度也就是无限的。这就跟海岸线是一个道理，海岸线不断缩小尺度的测量可以看成一次迭代，迭代的结果就是又得到一段类似结构的海岸线，然后再缩小尺度，又是一段一模一样的东西，所以在一定的程度上说海岸线其实是无限长的。

还有一种十分有意思的分形：混沌游戏（下面的例子只是其中的一种，你完全可以自己定义不同的规则）。

 

假设平面上有4个点，任取一点，比如选D点，然后抛骰子，如果是1，2就在AD的终点画一个点D1，如果3,4就在BD中点画，如果5,6就在CD中点画，然后迭代一定的次数就会出现这样的图形：

混沌游戏有一个特点，就是这是确定与随机的结合。规则是确定，取中点画点，但是画的点却是随机的，然后就出现了这样美妙的图像。然后你可以改规则，就可以发现很多奇妙的图形。

 

天地浑沌如鸡子，盘古生其中。万八千岁，天地开辟，阳清为天，阴浊为地。

——《三五历纪》

谁又知道造物主是不是在玩混沌游戏的时候无意间造就了整个世界呢？又或者说自然就只有一条很简单的规则，所谓“道生一，一生二，二生三，三生万物”，何妨理解成在规则的一次次迭代中产生了混沌，混沌造就了万物。混沌和分形的思想给了我们另一种有别传统因果律的思维方式。给那种所谓的只要怎么怎么样，就会怎么怎么样的论断产生了巨大的冲击。诚然只要后面的规则是确定，但是谁又知道会不会产生混沌呢？历史的大潮涛涛向前，我们都不过是滚滚的浪花中的一滴水。我们常说历史有所谓的大势所趋，可否理解为“大势”便是历史系统中一个确定的“规则”，而每个人在这个系统中的作用都微不足道。我们也常说“时势造英雄”，或者说“英雄造时势”，又可否认为这是一些特殊值，然后通过反馈机制，在历史大潮的迭代中产生了混沌效应，从而推动了历史的浪潮朝着既定的方向发展。看似偶然，实则必然。随机性和确定性的结合，世界也许就是因为不确定而更显的美丽吧。