线段树模板
本文只是自己存的模板,来源于https://www.cnblogs.com/xenny/p/9801703.html;
想学习线段树的请前往大佬的博客。
#include<bits/stdc++.h>
using namespace std;
const int maxn=100005;
int a[maxn],t[maxn<<2];
void Pushup(int k)
{
t[k]=max(t[k<<1],t[k<<1|1]);
}
void build(int l,int r,int k)//建树
{
if(l==r)
t[k]=a[l];
else
{
int mid=l+((r-l)>>1);
build(l,mid,k<<1);
build(mid+1,r,k<<1|1);
Pushup(k);
}
}
void upedge(int p,int v,int l,int r,int k)//点更新
{
if(l==r)
{
a[k]+=v;
t[k]+=v;
}
else
{
int mid=l+((r-l)>>1);
if(p<=mid)
upedge(p,v,l,mid,k<<1);
else
upedge(p,v,mid+1,r,k<<1|1);
Pushup(k);
}
}
int lazy[maxn<<1];
void Pushdown(int k)
{
if(lazy[k])
{
lazy[k<<1]+=lazy[k];
lazy[k<<1|1]+=lazy[k];
t[k<<1]+=lazy[k];
t[k<<1|1]+=lazy[k];
lazy[k]=0;
}
}
void downedge(int L,int R,int v,int l,int r,int k)//区间更新
{
if(l>=L&&r<=R)
{
lazy[k]+=v;
t[k]+=v;
}
else
{
Pushdown(k);
int mid=l+((r-l)>>1);
if(L<=mid)
downedge(L,R,v,l,mid,k<<1);
if(R>mid)
downedge(L,R,v,mid+1,r,k<<1|1);
Pushup(k);
}
}
int query(int L,int R,int l,int r,int k)//区间查询
{
if(l>=L&&r<=R)
return t[k];
else
{
Pushdown(k);
int res=-1e9+7;
int mid=l+((r-l)>>1);
if(L<=mid)
res=max(res,query(L,R,l,mid,k<<1));
if(R>mid)
res=max(maxn,query(L,R,mid+1,r,k<<1|1));
return res;
}
}
区间和
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn = 1e5 + 10;
ll n, m;
ll a[maxn], t[maxn << 2], lazy[maxn << 2];
void Pushup(ll k)
{
t[k] = t[k << 1] + t[k << 1 | 1];
}
void build(ll l, ll r, ll k)
{
if (l == r)
t[k] = a[l];
else
{
ll mid = l + ((r - l) >> 1);
build(l, mid, k << 1);
build(mid+1, r, k << 1 | 1);
Pushup(k);
}
}
void Pushdown(ll k,ll l,ll r)
{
if (lazy[k])
{
ll mid=l+((r-l)>>1);
lazy[k << 1] += lazy[k];
lazy[k << 1 | 1] += lazy[k];
t[k << 1] += lazy[k]*(mid-l+1);
t[k << 1 | 1] += lazy[k]*(r-mid);
lazy[k]=0;
}
}
void update(ll L, ll R, ll v, ll l, ll r, ll k)
{
if (L <= l && r <= R)
{
lazy[k] += v;
t[k] += v*(r-l+1);
}
else
{
Pushdown(k,l,r);
ll mid = l + ((r - l) >> 1);
if (L <= mid)
update(L, R, v, l, mid, k << 1);
if (mid< R)
update(L, R, v, mid + 1, r, k << 1 | 1);
Pushup(k);
}
}
ll query(ll L, ll R, ll l, ll r, ll k)
{
if (L <= l && r <= R)
return t[k];
else
{
Pushdown(k,l,r);
ll res = 0;
ll mid = l + ((r - l) >> 1);
if (L <= mid)
res += query(L, R, l, mid, k << 1);
if (R > mid)
res += query(L, R, mid + 1, r, k << 1 | 1);
return res;
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (ll i = 1; i <= n; i++)
cin >> a[i];
build(1, n, 1);
for(ll i=1;i<=m;i++)
{
ll check,u,v,w;
cin>>check;
if(check==1)
{
cin>>u>>v>>w;
update(u,v,w,1,n,1);
}
else if(check==2)
{
cin>>u>>v;
cout<<query(u,v,1,n,1)<<'\n';
// for(ll j=1;j<=9;j++)
// cout<<t[j]<<' ';
// cout<<'\n';
}
}
return 0;
}
如题,已知一个数列,你需要进行下面三种操作:
-
将某区间每一个数乘上 xx
-
将某区间每一个数加上 xx
-
求出某区间每一个数的和
输入格式
第一行包含三个整数 n,m,pn,m,p,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 nn 个用空格分隔的整数,其中第 ii 个数字表示数列第 ii 项的初始值。
接下来 mm 行每行包含若干个整数,表示一个操作,具体如下:
操作 11: 格式:1 x y k 含义:将区间 [x,y][x,y] 内每个数乘上 kk
操作 22: 格式:2 x y k 含义:将区间 [x,y][x,y] 内每个数加上 kk
操作 33: 格式:3 x y 含义:输出区间 [x,y][x,y] 内每个数的和对 pp 取模所得的结果
输出格式
输出包含若干行整数,即为所有操作 33 的结果。
输入输出样例
输入 #1
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4输出 #1
17
2说明/提示
【数据范围】
对于 30\%30% 的数据:n \le 8n≤8,m \le 10m≤10
对于 70\%70% 的数据:n \le 10^3n≤103,m \le 10^4m≤104
对于 100\%100% 的数据:n \le 10^5n≤105,m \le 10^5m≤105
除样例外,p = 571373p=571373
(数据已经过加强^_^)
样例说明:
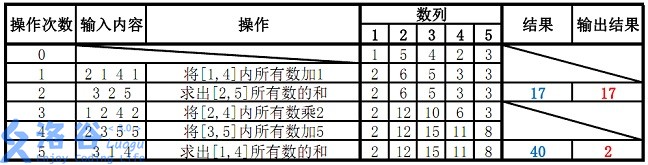
故输出应为 1717、22( 40 \bmod 38 = 240mod38=2 )
大佬题解 https://www.cnblogs.com/Renyi-Fan/p/8135010.html
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int mod;
ll a[100007];
struct node{
ll v,mul,add;
}st[400007];
void Pushup(int k)
{
st[k].v=(st[k<<1].v+st[k<<1|1].v)%mod;
}
void bt(int k,int l,int r)
{
st[k].mul=1,st[k].add=0;
if(l==r){
st[k].v=a[l];
}
else{
int mid=l+((r-l)>>1);
bt(k<<1,l,mid);
bt(k<<1|1,mid+1,r);
Pushup(k);
}
st[k].v%=mod;
}
void pushdown(int k,int l,int r)
{
int mid=l+((r-l)>>1);
st[k<<1].v=(st[k<<1].v*st[k].mul+st[k].add*(mid-l+1))%mod;
st[k<<1|1].v=(st[k<<1|1].v*st[k].mul+st[k].add*(r-mid))%mod;
st[k<<1].mul=(st[k<<1].mul*st[k].mul)%mod;
st[k<<1|1].mul=(st[k<<1|1].mul*st[k].mul)%mod;
st[k<<1].add=(st[k<<1].add*st[k].mul+st[k].add)%mod;
st[k<<1|1].add=(st[k<<1|1].add*st[k].mul+st[k].add)%mod;
st[k].mul=1;
st[k].add=0;
}
void ud1(int k, int l, int r, int L, int R, long long v){
if(R<l || r<L){
return ;
}
if(L<=l && r<=R){
st[k].v=(st[k].v*v)%mod;
st[k].mul=(st[k].mul*v)%mod;
st[k].add=(st[k].add*v)%mod;
return ;
}
pushdown(k, l, r);
int mid=l+((r-l)>>1);
ud1(k<<1, l, mid, L, R, v);
ud1(k<<1|1, mid+1, r, L, R, v);
Pushup(k);
return ;
}
void ud2(int k, int l, int r, int L, int R, long long v){
if(R<l || r<L){
return ;
}
if(L<=l && r<=R){
st[k].add=(st[k].add+v)%mod;
st[k].v=(st[k].v+v*(r-l+1))%mod;
return ;
}
pushdown(k, l, r);
int mid=l+((r-l)>>1);
ud2(k*2, l, mid, L, R, v);
ud2(k*2+1, mid+1, r, L, R, v);
Pushup(k);
return ;
}
long long query(int root, int l, int r, int L, int R){
if(R<l || r<L){
return 0;
}
if(L<=l && r<=R){
return st[root].v;
}
pushdown(root, l, r);
int mid=l+((r-l)>>1);
return (query(root*2, l, mid, L, R)+query(root*2+1, mid+1, r, L, R))%mod;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int n,m;
cin>>n>>m>>mod;
for(int i=1;i<=n;i++)
cin>>a[i];
bt(1,1,n);
while(m--)
{
int check,u,v;
ll w;
cin>>check;
if(check==1)
{
cin>>u>>v>>w;
ud1(1,1,n,u,v,w);
}
else if(check==2)
{
cin>>u>>v>>w;
ud2(1,1,n,u,v,w);
}
else
{
cin>>u>>v;
cout<<query(1,1,n,u,v)<<'\n';
}
}
return 0;
}线段树求最大连续子段和
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<vector>
#include<queue>
#include<cmath>
#include<set>
#include<cmath>
#include<stack>
#include <iomanip>
#include<unordered_map>
using namespace std;
#define int long long
#define ull unsigned long long
#define unmap unordered_map
#define endl '\n'
#define ls (p << 1)
#define rs (p << 1 | 1)
#define lowbit(x) x&(-x)
#define s_n (int)s.size()
#define two int a,b,c;cin>>a>>b>>c;add(a,b,c);add(b,a,c);
#define one int a,b,c;cin>>a>>b>>c;add(a,b,c);
const int maxn=5e5+5,mod=1e9+7;
typedef pair<int,int> PII;
int a[maxn];
int n,m;
struct node {
int sum,lmax,rmax,dat;
}tr[maxn<<2];
void pushup(int p) {
tr[p].sum=tr[ls].sum+tr[rs].sum;
tr[p].lmax=max(tr[ls].lmax,tr[ls].sum+tr[rs].lmax);
tr[p].rmax=max(tr[rs].rmax,tr[rs].sum+tr[ls].rmax);
tr[p].dat=max({tr[ls].dat,tr[rs].dat,tr[ls].rmax+tr[rs].lmax});
}
void build(int p,int l,int r) {
if(l==r) {
tr[p].dat=tr[p].sum=tr[p].lmax=tr[p].rmax=a[l];
} else {
int mid=l+r>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(p);
}
}
void update(int k,int v,int l,int r,int p) {
if(l==r) {
tr[p].dat=tr[p].sum=tr[p].lmax=tr[p].rmax=v;
a[l]=v;
} else {
int mid=l+r>>1;
if(k<=mid) update(k,v,l,mid,ls);
else update(k,v,mid+1,r,rs);
pushup(p);
}
}
node query(int p,int L,int R,int l,int r) {
if(L<=l&&r<=R) return tr[p];
else {
int mid=l+r>>1;
int ans=-1e18;
node a,b,c;
a.dat=a.sum=a.lmax=a.rmax=ans;
b.dat=b.sum=b.lmax=b.rmax=ans;
c.sum=0;
if(L<=mid) {
a=query(ls,L,R,l,mid);
c.sum+=a.sum;
}
if(R>mid) {
b=query(rs,L,R,mid+1,r);
c.sum+=b.sum;
}
c.dat=max({a.dat,b.dat,a.rmax+b.lmax});
c.lmax=max(a.lmax,a.sum+b.lmax);
if(L>mid)
c.lmax=max(c.lmax,b.lmax);
c.rmax=max(b.rmax,b.sum+a.rmax);
if(R<=mid)
c.rmax=max(c.rmax,a.rmax);
return c;
}
}
void solve() {
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
while(m--) {
int k,a,b;
cin>>k>>a>>b;
if(k==2) {
update(a,b,1,n,1);
} else {
if(a>b)swap(a,b);
cout<<query(1,a,b,1,n).dat<<endl;
}
}
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int ONE_PIECE=1;
while(ONE_PIECE--) {
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号