建图优化
缩点
之前提过,不再多说 link
去无用边优化建图
最为简单的就是去重边,删自环。
稍微升级一点就是最小生成树。
一个例题 CF1095F Make It Connected solution
前后缀优化建图
解决对于一个点向一段前缀或者后缀连边的问题。
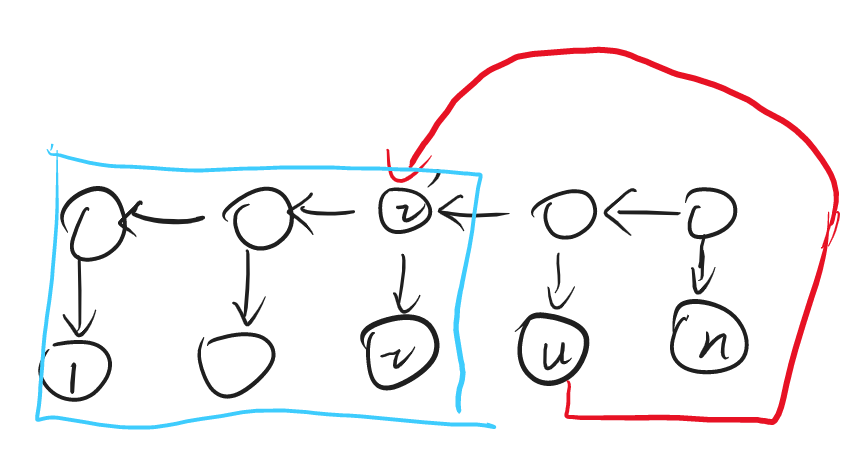
具体的做法是将整个区间建立一条长为 \(n\) 的虚链。这条虚链从后往前(这种是前缀,后缀是从前往后)连单向边,每个虚链上的点向真正的点连边。
那么我们连边(打个比方,从 \(u\) 连到前缀 \([1,v]\))就只需要从 \(u\) 的实点向 \(v\) 的虚点连一条边即可。如果有边权的话我们只在下图中红边赋予边权,其他边边权为 \(0\)。复杂度 \(O(m)\)
线段树优化建图
可以解决区间、点之间连边的问题。复杂度都是 \(O(m\log n)\) 的。
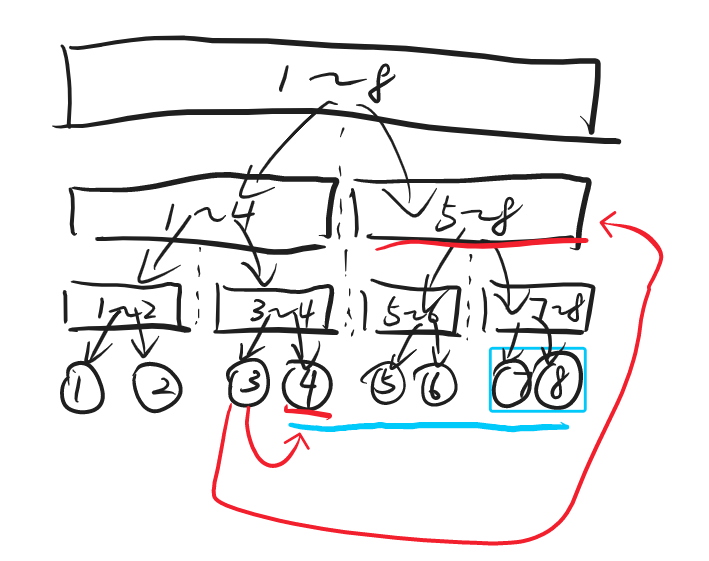
点连向区间
建立一颗父亲向儿子连单向边的入边线段树,叶子维护实点。
接下来我们直接像普通的查询区间一样,在树中查找出 \(O(\log n)\) 个区间,然后点分别向这几个区间连边即可。
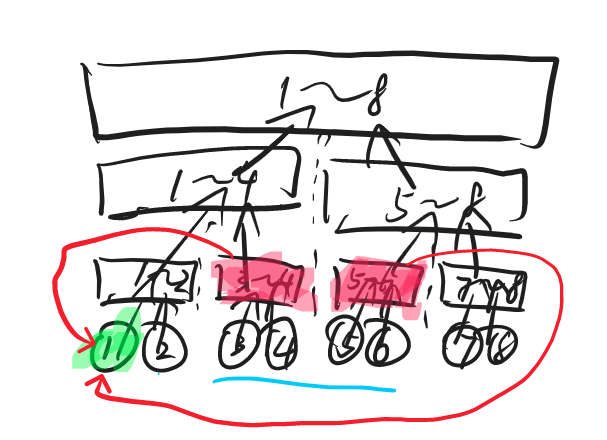
区间连向点
建立一颗儿子向父亲连单向边的出边线段树,叶子维护实点。
线段树中找到区间然后区间分别向这个点连边即可。
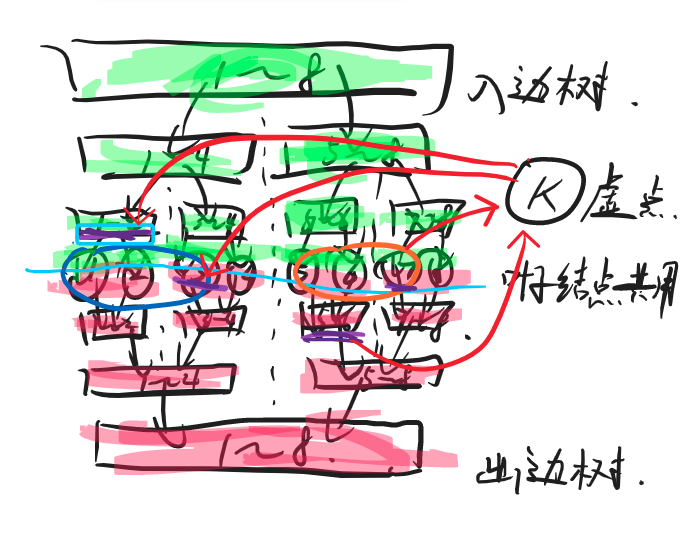
区间连区间
同时维护入边树和出边树即可。但是直接连是 \(O(\log^2 n)\) 的,显得比较低端。
考虑统一建一个虚点让区间往那里连边即可。这个叶子节点共用只要两个树中叶子节点维护的编号相同即可。
注意一下这里的边是需要开到 \(O(2\log n )\) 的。
参考代码:
#include<bits/stdc++.h>
#define ll long long
#define db double
#define filein(a) freopen(#a".in","r",stdin)
#define fileot(a) freopen(#a".out","w",stdout)
#define sky fflush(stdout);
#define gc getchar
#define pc putchar
#define Better_IO true
namespace IO{
#if Better_IO==true
char buf[(1<<20)+3],*p1(buf),*p2(buf);
const int lim=1<<20;
inline char gc(){
if(p1==p2) p2=(p1=buf)+fread(buf,1,lim,stdin);
return p1==p2?EOF:*p1++;
}
#define pc putchar
#else
#define gc getchar
#define pc putchar
#endif
inline bool blank(const char &c){
return c==' ' or c=='\n' or c=='\t' or c=='\r' or c==EOF;
}
inline void gs(char *s){
char ch=gc();
while(blank(ch) ) {ch=gc();}
while(!blank(ch) ) {*s++=ch;ch=gc();}
*s=0;
}
inline void gs(std::string &s){
char ch=gc();s+='#';
while(blank(ch) ) {ch=gc();}
while(!blank(ch) ) {s+=ch;ch=gc();}
}
inline void ps(char *s){
while(*s!=0) pc(*s++);
}
inline void ps(const std::string &s){
for(auto it:s)
if(it!='#') pc(it);
}
template<class T>
inline void read(T &s){
s=0;char ch=gc();bool f=0;
while(ch<'0'||'9'<ch) {if(ch=='-') f=1;ch=gc();}
while('0'<=ch&&ch<='9') {s=s*10+(ch^48);ch=gc();}
if(ch=='.'){
db p=0.1;ch=gc();
while('0'<=ch&&ch<='9') {s=s+p*(ch^48);p*=0.1;ch=gc();}
}
s=f?-s:s;
}
template<class T,class ...A>
inline void read(T &s,A &...a){
read(s);read(a...);
}
};
using IO::read;
using IO::gs;
using IO::ps;
const int N=1e5+3;
const int N2=(N<<3);
const int M=(N<<3)+N*17;
const ll inf=1e18;
int n,m,s;
int head[N2],nxt[M];
struct Edge{
int u,v,w;
}to[M];
int Etot=-1;
inline void link(int u,int v,int w){
nxt[++Etot]=head[u];
head[u]=Etot;
to[Etot]={u,v,w};
}
int tot;
#define lc(x) (x<<1)
#define rc(x) (x<<1|1)
struct SegTree_in{
struct node{
int l,r,mid;
int id;
}t[N<<2];
inline void build(int x,int l,int r){
t[x].l=l;t[x].r=r;t[x].mid=(l+r)>>1;
if(l==r){
t[x].id=l;
return;
}else t[x].id=++tot;
build(lc(x),l,t[x].mid);
build(rc(x),t[x].mid+1,r);
link(t[x].id,t[lc(x)].id,0);
link(t[x].id,t[rc(x)].id,0);
}
inline void Link(int x,int u,int l,int r,int w){
if(l<=t[x].l and t[x].r<=r){
link(u,t[x].id,w);
return;
}
if(l<=t[x].mid) Link(lc(x),u,l,r,w);
if(t[x].mid+1<=r) Link(rc(x),u,l,r,w);
}
}in;
struct SegTree_ot{
struct node{
int l,r,mid;
int id;
}t[N<<2];
inline void build(int x,int l,int r){
t[x].l=l;t[x].r=r;t[x].mid=(l+r)>>1;
if(l==r){
t[x].id=l;
return;
}else t[x].id=++tot;
build(lc(x),l,t[x].mid);
build(rc(x),t[x].mid+1,r);
link(t[lc(x)].id,t[x].id,0);
link(t[rc(x)].id,t[x].id,0);
}
inline void Link(int x,int u,int l,int r,int w){
if(l<=t[x].l and t[x].r<=r){
link(t[x].id,u,w);
return;
}
if(l<=t[x].mid) Link(lc(x),u,l,r,w);
if(t[x].mid+1<=r) Link(rc(x),u,l,r,w);
}
}ot;
#undef lc
#undef rc
ll dis[N2];
bool vis[N2];
struct node{
int x;ll val;
inline friend bool operator < (node x,node y){
return x.val>y.val;
}
};
inline void Dijkstra(){
static std::priority_queue<node>q;
for(int i=1;i<=tot;++i){
dis[i]=inf;
}
dis[s]=0;
q.push({s,0});
while(!q.empty() ){
int u=q.top().x;q.pop();
if(vis[u]) continue;vis[u]=1;
for(int i=head[u];~i;i=nxt[i]){
int v=to[i].v,w=to[i].w;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
if(!vis[v]) q.push({v,dis[v]});
}
}
}
}
int main(){
filein(a);fileot(a);
read(n,m,s);
tot=n;
memset(head,-1,sizeof(head) );
in.build(1,1,n);ot.build(1,1,n);
for(int i=1;i<=m;++i){
int op,u,v,l,r,w;
read(op);
if(op==1){
read(u,v,w);
link(u,v,w);
}
if(op==2){
read(u,l,r,w);
in.Link(1,u,l,r,w);
}
if(op==3){
read(u,l,r,w);
ot.Link(1,u,l,r,w);
}
}
Dijkstra();
for(int i=1;i<=n;++i){
printf("%lld ",dis[i]==inf?-1:dis[i]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号