wqs二分
我们通过一道例题引入。
引入
CF1279F New Year and Handle Change
题目大意:给出长度为 \(n\) 一个01串(表现为大小写),可以最多选择 \(m\) 个 \(s\) 长度的子串,全部变为0或1。求操作后的 \(\min(cnt_0 , cnt_1)\) 的最小值
\(1 \le n,m,s ≤10^6\)
题解
我们可以简单地想到可以分开考虑全变为 \(1\) 和全变为 \(0\) 。然后对于这两种情况我们可以很快的想到一个 \(O(n^2)\) 的DP。暂且只考虑全变 \(1\),全变 \(0\) 是一样的,我们设 \(dp_{i,j}\) 表示我们在区间 \([i-s+1,i]\) 执行第 \(j\) 次操作的最大的能够抹除的 \(0\) 的个数。那么我们很快可以得到DP的转移式:
其中 \(sum_i\) 表示 \(0\) 的个数的前缀和。统计答案就直接 \(sum_n-dp_{n,m}\) 即可。
但是看看数据范围就发现不行,要考虑优化。发现随着 \(m\) 的增大,我们可以删去的 \(0\) 必然单调不减,且由于 \(m\) 越大,之后操作能消去的 \(0\) 逐渐变少,所以若我们记 \(g(x)\) 表示 \(m\) 次操作能够最多消去的 \(0\) 的个数,这个函数虽然显然具有单调性,但是更为重要的是其具有凸性,即我们用一条切线去切这个函数图象,它上面的每个点都可以被切到。数学化的说,求增长速率逐渐减缓,下降速度增快(或者反过来也可以),数字化的说,就是其差分数组具有单调性。
有了这个性质,我们就可以进行 wqs二分 。这个性质是 wqs二分 进行的前提。实在不行可以打表去发现凸性。
它具体是怎么做的呢?它的思想就是,我们通过一些操作除去限制,然后我们可以容易地用DP求出。之后再通过一些操作转换到我们的带限制的最优解。(我这里采用的是几何化+意义化理解,而并非形象化理解,喜欢形象化理解的可以去看其他人的博客)
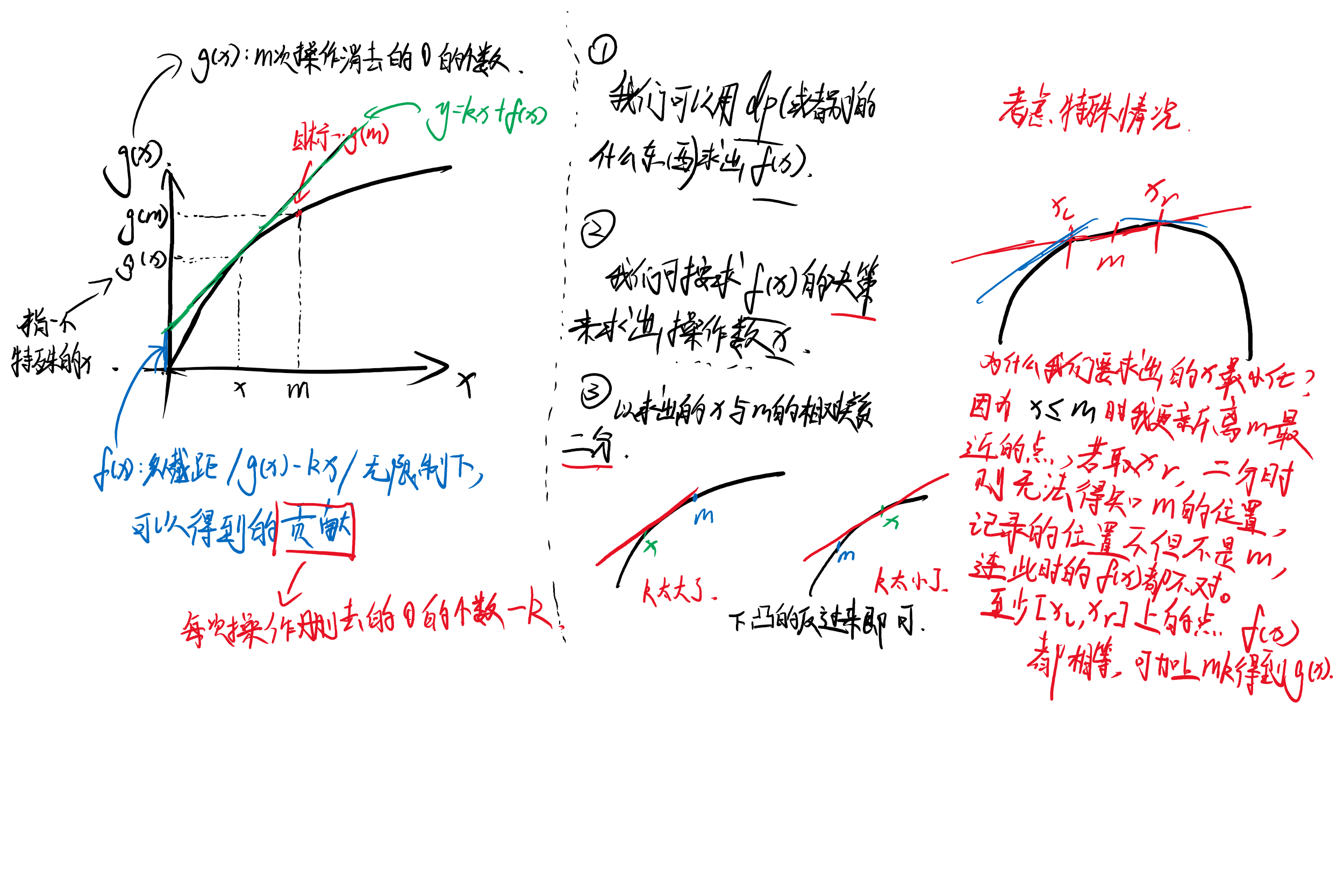
具体来说,我们先把 \(m\) 放在 \(g(x)\) 上,现在我们的目标就是 \(g(m)\) 。但是 \((m,g(m)\ )\) 具体在哪我们不得而知,因此我们考虑通过一些转换来求解它。
由于 \(g(x)\) 具有凸性,显然我们可以使用直线去切它,而此时直线的纵截距和切点的横坐标都关于斜率大小具有单调性,所以我们想到要去二分斜率。尽管我们二分完也暂且不知道这个切点和纵截距在哪,但是我们继续考虑转换。我们记切在横坐标为 \(x\) 的点上的直线的纵截距为 \(f(x)\) ,考虑纵截距 \(f(x)\) 的在几何上得到的代数意义: \(f(x)=g(x)-kx\) 。然后我们观察这个式子,然后思考 \(g(x),f(x)\) 的现实意义。
由于我们知道 \(g(x)\) 表示 \(x\) 次操作能够最多消去的 \(0\) 的个数,那么可以发现 \(f(x)\) 的现实意义为:每次消去的 \(0\) 的个数 \(-k\) 作为贡献,在 \(x\) 次操作后得到的贡献的最大值。这个看着是有一个 \(x\) 的限制,但是由于这个 \(x\) 是未知数,我们现在反而是要求 \(x\) ,所以 \(f(x)\) 作为截距的意义就是:每次消去的 \(0\) 的个数 \(-k\) 作为贡献得到的贡献的最大值。这个东西我们可以通过上面的DP删去操作次数的第二维求出,复杂度 \(O(n)\)。 然后反推一下可以求出 \(g(x)\) 。
你以为结束了?没有。我们还不知道那个位置是 \(m\) ,怎么算出 \(g(m)\) ,所以我们DP \(f(x)\) 时,我们按照决策及其意义统计操作次数即可。然后我们二分的时候检查操作次数和 \(m\) 的大小关系,然后按照这个调整斜率,以此移动切点的位置即可。复杂度易证 \(O(n\log n)\)。
但是要注意的是,我们统计出的操作次数一定要最小化,不然会出现问题。原因我会同上面讨论的问题的图解一同给出。下面给出图解:
参考代码
#include<bits/stdc++.h>
#define ll long long
#define db double
#define filein(a) freopen(#a".in","r",stdin)
#define fileot(a) freopen(#a".out","w",stdout)
#define sky fflush(stdout)
#define gc getchar
#define pc putchar
namespace IO{
template<class T>
inline void read(T &s){
s=0;char ch=gc();bool f=0;
while(ch<'0'||'9'<ch) {if(ch=='-') f=1;ch=gc();}
while('0'<=ch&&ch<='9') {s=s*10+(ch^48);ch=gc();}
if(ch=='.'){
db p=0.1;ch=gc();
while('0'<=ch&&ch<='9') {s=s+p*(ch^48);ch=gc();}
}
s=f?-s:s;
}
template<class T,class ...A>
inline void read(T &s,A &...a){
read(s);read(a...);
}
inline bool blank(char c){
return c==' ' or c=='\t' or c=='\n' or c=='\r' or c==EOF;
}
inline void gs(std::string &s){
s+='#';char c=gc();
while(blank(c) ) c=gc();
while(!blank(c) ){
s+=c;c=gc();
}
}
inline void gs(char *s){
char ch=gc();
while(blank(ch) ) {ch=gc();}
while(!blank(ch) ){
*s++=ch;ch=gc();
}
}
};
using IO::read;
using IO::gs;
const int N=1e6+3;
const int inf=1e9;
int n,m,s;
char c[N];
int sum[N];
int f[N],g[N];
int ans=inf;
inline int check(int p,bool op){
for(int i=1;i<=n;++i){
int x=f[std::max(i-s,0)]+sum[i]-sum[std::max(i-s,0)]-p;
f[i]=std::max(f[i-1],x);
if(x<f[i-1]) g[i]=g[i-1];
if(x>f[i-1]) g[i]=g[std::max(i-s,0)]+1;
if(x==f[i-1]) g[i]=std::min(g[i-1],g[std::max(i-s,0)]+1);
}
if(op) ans=std::min(ans,sum[n]-f[n]-m*p);
return g[n];
}
int main(){
filein(a);fileot(a);
read(n,m,s);
gs(c+1);
for(int i=1;i<=n;++i){
sum[i]=sum[i-1]+('A'<=c[i] and c[i]<='Z');
}
int l=0,r=n,res=0;
while(l<=r){
int mid=(l+r)>>1;
if(check(mid,0)<=m){
r=mid-1;res=mid;
}else{
l=mid+1;
}
}
check(res,1);
for(int i=1;i<=n;++i){
sum[i]=sum[i-1]+('a'<=c[i] and c[i]<='z');
}
l=0,r=n,res=0;
while(l<=r){
int mid=(l+r)>>1;
if(check(mid,0)<=m){
r=mid-1;res=mid;
}else{
l=mid+1;
}
}
check(res,1);
printf("%d\n",ans);
return 0;
}
例题分析
题目大意:给你一个 \(n\) 个点 \(m\) 条边的的无向带权连通图,每条边是黑色或白色。让你求一棵最小权的恰好有 \(d\) 条白色边的生成树。
\(n\le5e4,m\le 1e5,w\le 100\)
题解
这个题虽然不需要DP,但是用到了wqs二分。
我们设 \(g(x)\) 表示选择 \(x\) 条白边的最小生成树大小。这个函数具有凸性,我们假设原图的最小生成树中包含 \(z\) 条白边,那么 \(x\) 越接近 \(z\) ,就越接近这个最小生成树的形态,由于我们 \(x\) 离 \(z\) 越远,就越必须现在那些能够被称为骤增的白边。说这么多,最主要的是 \(x\) 远离 \(z\) 的过程中,这个凸壳的走势绝对不会减缓,因为增加量大的都被 Kruskal 放到放到后面去了。
那么截距 \(f(x)\) 意义可得:白边边权减少 \(k\) 的情况下,生成树边权最大值。这个可以 Kruskal 求,横坐标也可顺便统计。然后就没什么好说的了。然后提一句二分范围,只有在比右端点最大的单次操作变化两大,左端点比最大减少量小即可。复杂度 \(O(n\log n\log w_{max})\)。
参考代码
#include<bits/stdc++.h>
#define ll long long
#define db double
#define filein(a) freopen(#a".in","r",stdin)
#define fileot(a) freopen(#a".out","w",stdout)
#define sky fflush(stdout)
#define gc getchar
#define pc putchar
namespace IO{
template<class T>
inline void read(T &s){
s=0;char ch=gc();bool f=0;
while(ch<'0'||'9'<ch) {if(ch=='-') f=1;ch=gc();}
while('0'<=ch&&ch<='9') {s=s*10+(ch^48);ch=gc();}
if(ch=='.'){
db p=0.1;ch=gc();
while('0'<=ch&&ch<='9') {s=s+p*(ch^48);ch=gc();}
}
s=f?-s:s;
}
template<class T,class ...A>
inline void read(T &s,A &...a){
read(s);read(a...);
}
inline bool blank(char c){
return c==' ' or c=='\t' or c=='\n' or c=='\r' or c==EOF;
}
inline void gs(std::string &s){
s+='#';char c=gc();
while(blank(c) ) c=gc();
while(!blank(c) ){
s+=c;c=gc();
}
}
inline void gs(char *s){
char ch=gc();
while(blank(ch) ) {ch=gc();}
while(!blank(ch) ){
*s++=ch;ch=gc();
}
*s=0;
}
};
using IO::read;
using IO::gs;
const int N=5e4+3;
const int M=1e5+3;
int n,m,d;
struct Edge{
int u,v,w,c;
}e[M];
int fa[N];
int find(int x){
return x==fa[x]?x:fa[x]=find(fa[x]);
}
int ans=0;
inline int check(int k,bool op){
static int tmpk;
tmpk=k;
std::sort(e+1,e+1+m,[](Edge x,Edge y){
int vx=x.w+(x.c?-tmpk:0),vy=y.w+(y.c?-tmpk:0);
if(vx==vy) return x.c<y.c;
return vx<vy;
});
for(int i=1;i<=n;++i){
fa[i]=i;
}
int res=0,cnt=0;
for(int i=1;i<=m;++i){
int u=e[i].u,v=e[i].v;
if(find(u)!=find(v) ){
fa[find(v)]=find(u);
res+=e[i].w+(e[i].c?-k:0);
if(e[i].c) ++cnt;
}
}
if(op) ans=res+d*k;
return cnt;
}
int main(){
filein(a);fileot(a);
read(n,m,d);
for(int i=1;i<=m;++i){
int u,v,w,c;
read(u,v,w,c);
++u;++v;
e[i]={u,v,w,!c};
}
int l=-100,r=100,res=100;
while(l<=r){
int mid=(l+r)>>1;
if(check(mid,0)<=d){
l=mid+1;res=mid;
}else{
r=mid-1;
}
}
check(res,1);
printf("%d\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号