SPFA求最短路径

 

 最近在鼓捣蓝桥杯的题目，其中有一题是这样的。

  上个学期我已经学习了数据结构，在书上找到了迪杰斯拉特算法，但是发现自己漏了一个重要的条件，就是边考研为负的。这个算法对边为负数的情况无效。浴室通过度娘找到了一种万金油的方法，SPFA算法。

  这个算法是这样的，通过建立队列，来每次更新1到n的最短路径。

  代码如下： 

#include<iostream>
#include<string>
using namespace std;
#define N 20020
#define M 20020
#define inf 100000
int Q[M];
int cont=0;
int head[N];
float dis[N];
int front;
int rear;
int visited[N*M];
struct node
{
    int next;
    int to;
    float w;
}e[N];
void add(int from,int to,float weight)
{
    e[cont].to = to;
    e[cont].next = head[from];
    e[cont].w = weight;
    head[from] = cont++;
}
void SPFA(int t)
{
    int i, j, temp;
    for ( i = 1; i <= t; i++)
        dis[i] = inf;
    front = 0;
    rear = 1;
    dis[1] = 0;
    visited[1] = 1;
    Q[front] = 1;
    while (front < rear)
    {
        temp = Q[front++];
        visited[temp] = 0;
        j = head[temp];
        while (j>-1)
        {
            if (dis[e[j].to] > e[j].w + dis[temp])
            {
                dis[e[j].to] = e[j].w + dis[temp];
                    if (!visited[e[j].to])
                    {
                        Q[rear++] = e[j].to;
                        visited[e[j].to] = 1;
                    }
            }
            j = e[j].next;
        }
    }
}
int main()
{
    int n, m;
    int v, u, l;
    cin >> n >> m;
    memset(Q, 0, sizeof(Q));
    memset(head, -1, sizeof(head));
    memset(visited, 0, sizeof(visited));
    for (int i = 1; i <= n; i++)
    {
        cin >> v >> u >> l;
        add(v, u, l);
    }
    SPFA(n);
    for (int i = 2; i <= n; i++)
        cout << dis[i]<<endl;
    system("pause");
    return 0;
}

 

其中，图是用链式超前星方式构造的。关于链式超星的资料：https://blog.csdn.net/acdreamers/article/details/16902023

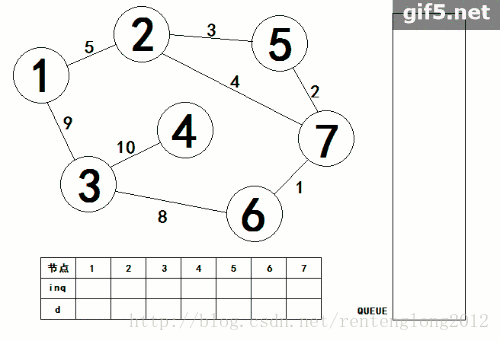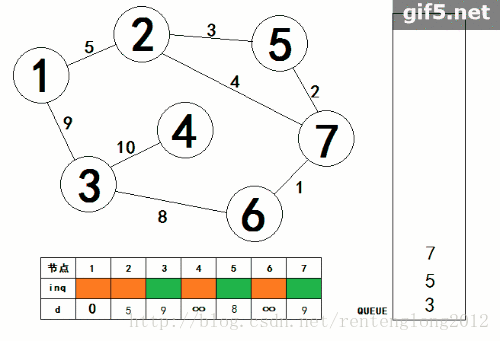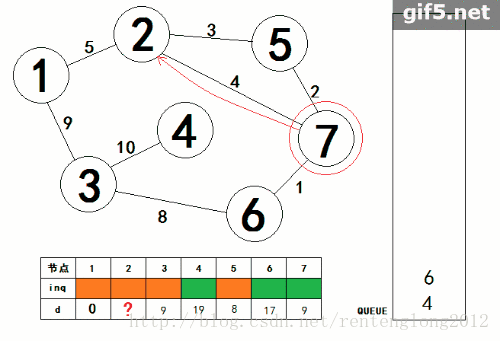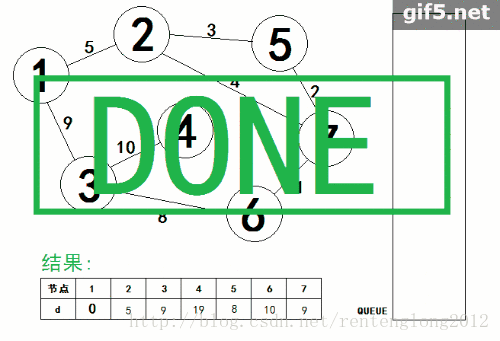
下面为SPFA算法的动态图，下面链接的这个博客写的非常好，有助于理解。

图片转载：

https://blog.csdn.net/rentenglong2012/article/details/78483662

另一篇也写地非常易于理解：

https://blog.csdn.net/sxy201658506207/article/details/78779045